Surface Area of Prisms And Cylinders Prism Polyhedron














- Slides: 18

Surface Area of Prisms And Cylinders

Prism: Polyhedron with two parallel, congruent bases Named after its base

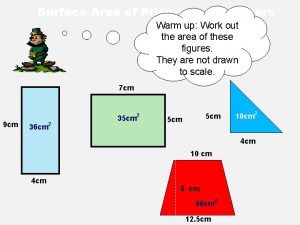
Surface area: Sum of the area of each face of the solid

Surface area: Sum of the area of each face of the solid Left Top Back Front Bottom Right

Lateral area: Area of each lateral face

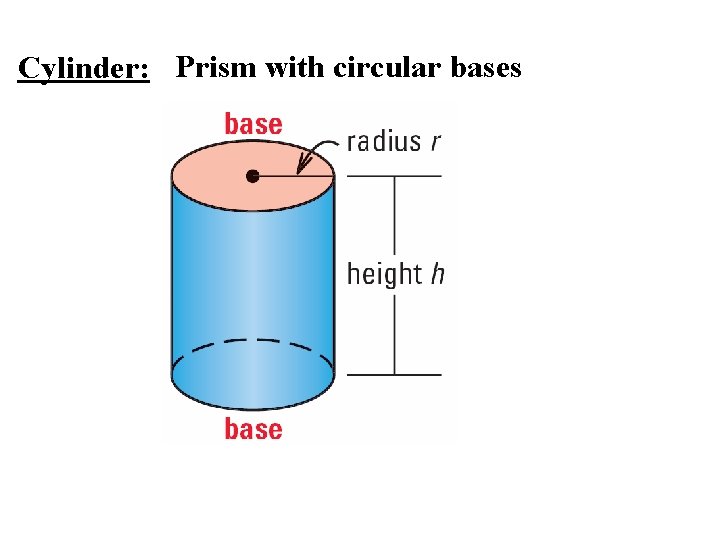
Cylinder: Prism with circular bases

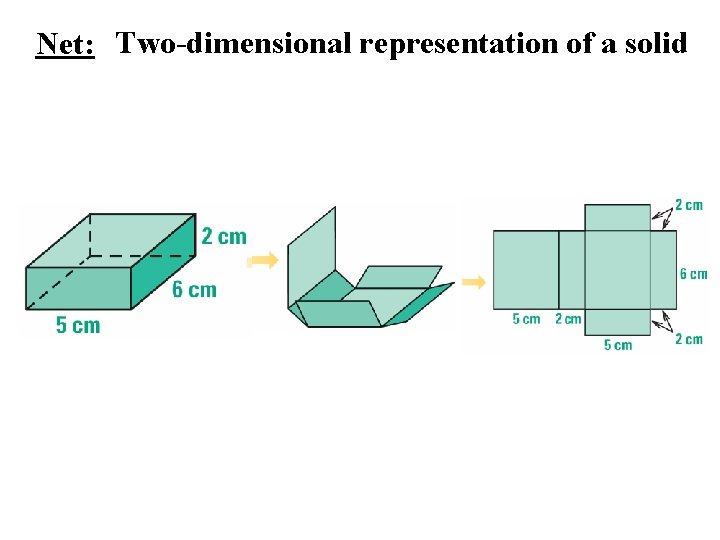
Net: Two-dimensional representation of a solid

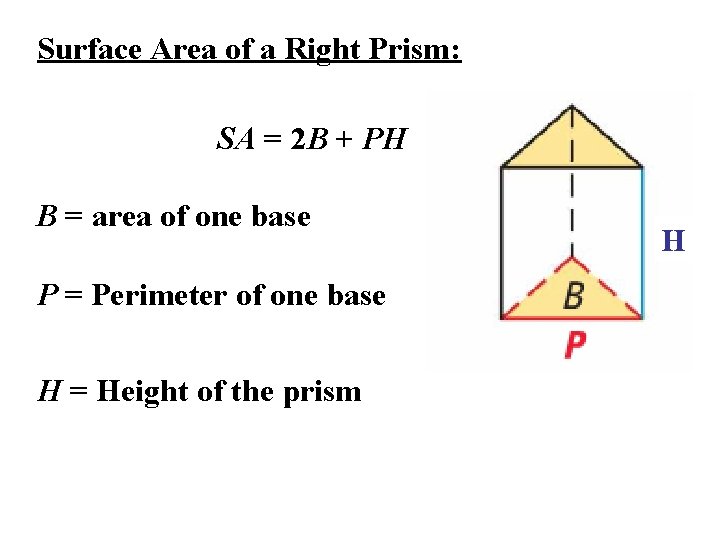
Surface Area of a Right Prism: SA = 2 B + PH B = area of one base P = Perimeter of one base H = Height of the prism H

Surface Area of a Right Cylinder: SA = 2 B + PH H

1. Name the solid that can be formed by the net. Cylinder

1. Name the solid that can be formed by the net. Triangular prism

1. Name the solid that can be formed by the net. rectangular prism

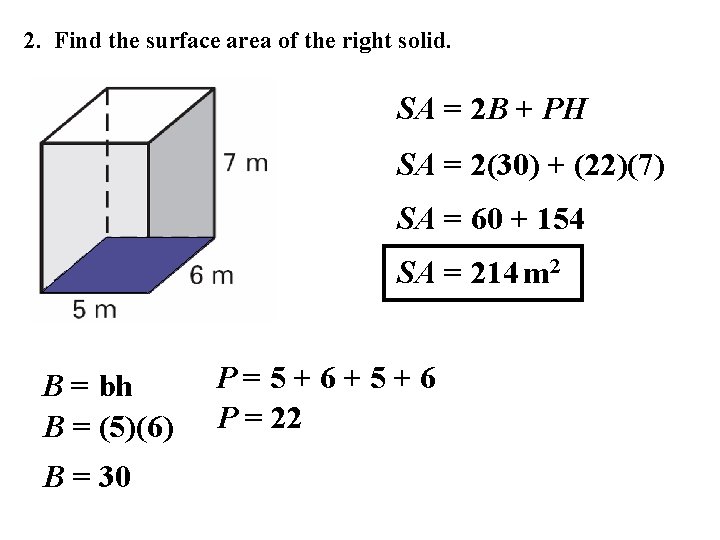
2. Find the surface area of the right solid. SA = 2 B + PH SA = 2(30) + (22)(7) SA = 60 + 154 SA = 214 m 2 B = bh B = (5)(6) B = 30 P=5+6+5+6 P = 22

2. Find the surface area of the right solid. 13 cm SA = Ph + 2 B SA = (5+12+13)(10) + 2(30) SA = (30)(10) + 2(30) SA = 300 = 60 SA = 360 cm 2 P = 5 + 12 + 13 P = 30

2. Find the surface area of the right solid. cm 2

2. Find the surface area of the right solid. 8 ft 12 ft ft 2

2. Find the surface area of the right solid. 9 ft 10 ft 6 ft 8 ft SA = Ph + 2 B SA = 2(24) + (24)(9) SA = 48 + 216 SA = 264 ft 2 P = 6 + 8 + 10 P = 24

2. Find the surface area of the right solid. A cylindrical bass drum has a radius of 5 inches and a depth of 12 inches. Find the surface area. 5 in 12 in in 2
 Surface area and volume of cylinders and prisms worksheet
Surface area and volume of cylinders and prisms worksheet Surface area of prisms and cylinders
Surface area of prisms and cylinders 10-6 surface area
10-6 surface area 11-2 surface area of prisms and cylinders
11-2 surface area of prisms and cylinders 10-4 surface area of prisms and cylinders
10-4 surface area of prisms and cylinders Surface area of prisms and cylinders
Surface area of prisms and cylinders 10-4 surface area of prisms and cylinders
10-4 surface area of prisms and cylinders Surface area problem solving
Surface area problem solving Lesson 12-2 surface areas of prisms and cylinders
Lesson 12-2 surface areas of prisms and cylinders Hexagonal prism volume calculator soup
Hexagonal prism volume calculator soup Name of prism
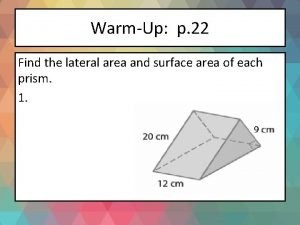
Name of prism Find the lateral area and surface area of each prism
Find the lateral area and surface area of each prism Lateral face
Lateral face Curved surface area and total surface area of cone
Curved surface area and total surface area of cone Volume of cylinders cones and spheres maze
Volume of cylinders cones and spheres maze 13-1 practice volumes of prisms and cylinders
13-1 practice volumes of prisms and cylinders Area of prisms
Area of prisms 12-4 volume of prisms and cylinders
12-4 volume of prisms and cylinders Volume of prisms and cylinders formula
Volume of prisms and cylinders formula