Structure from motion Structure from motion Given a





















- Slides: 53

Structure from motion

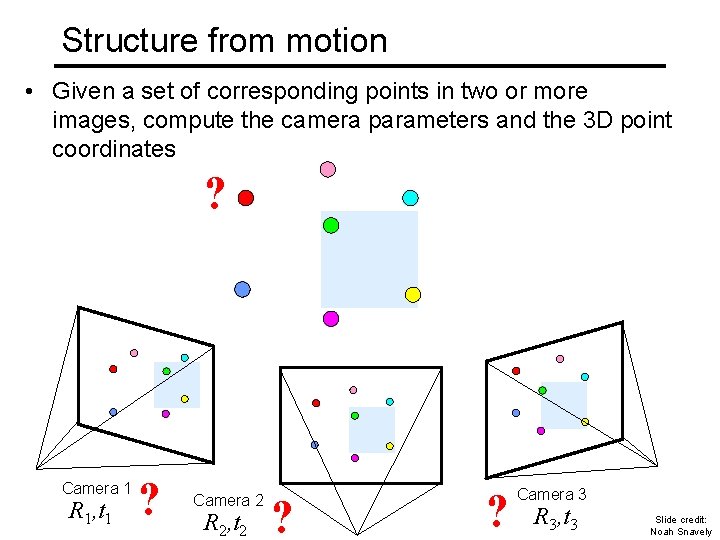
Structure from motion • Given a set of corresponding points in two or more images, compute the camera parameters and the 3 D point coordinates ? Camera 1 R 1, t 1 ? Camera 2 R 2, t 2 ? ? Camera 3 R 3, t 3 Slide credit: Noah Snavely

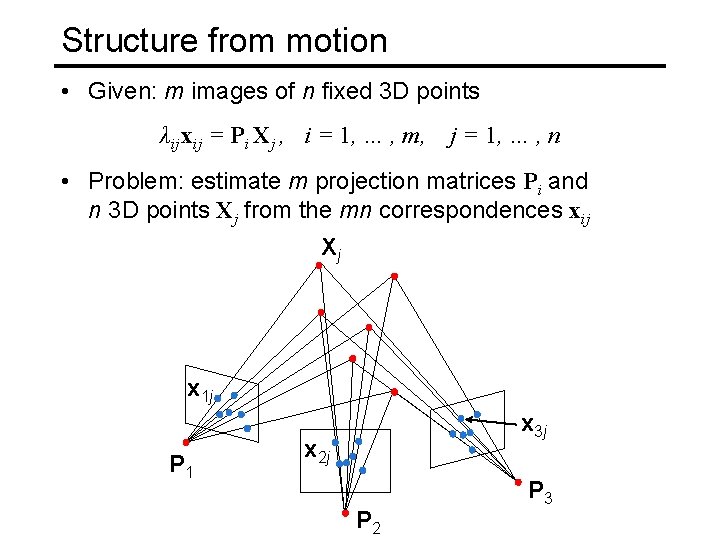
Structure from motion • Given: m images of n fixed 3 D points λij xij = Pi Xj , i = 1, … , m, j = 1, … , n • Problem: estimate m projection matrices Pi and n 3 D points Xj from the mn correspondences xij Xj x 1 j P 1 x 3 j x 2 j P 2 P 3

Outline • Reconstruction ambiguities • Affine structure from motion • Factorization • Projective structure from motion • Bundle adjustment • Modern structure from motion pipeline

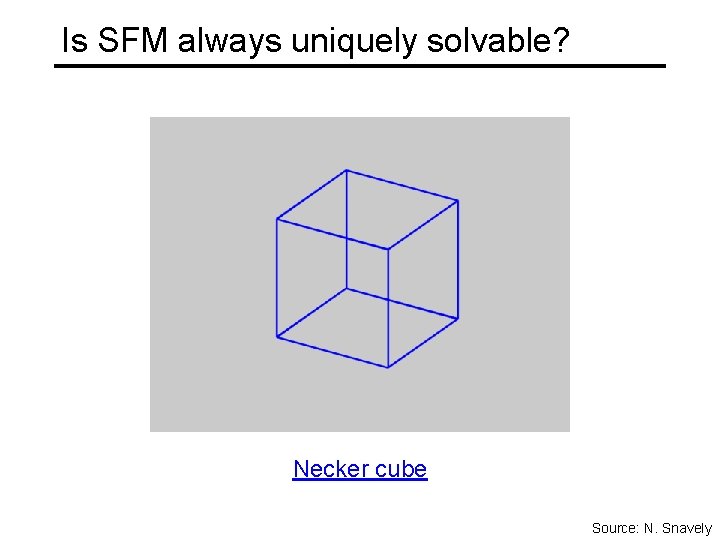
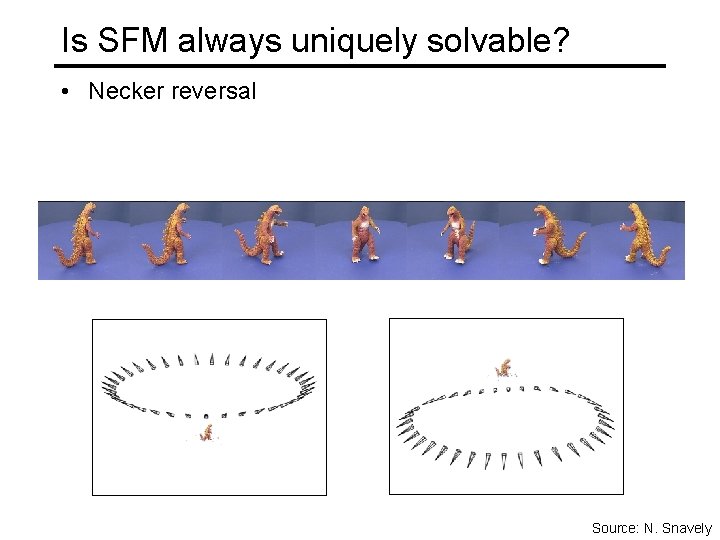
Is SFM always uniquely solvable? Necker cube Source: N. Snavely

Is SFM always uniquely solvable? • Necker reversal Source: N. Snavely

Structure from motion ambiguity • If we scale the entire scene by some factor k and, at the same time, scale the camera matrices by the factor of 1/k, the projections of the scene points in the image remain exactly the same: It is impossible to recover the absolute scale of the scene!

Structure from motion ambiguity • If we scale the entire scene by some factor k and, at the same time, scale the camera matrices by the factor of 1/k, the projections of the scene points in the image remain exactly the same • More generally, if we transform the scene using a transformation Q and apply the inverse transformation to the camera matrices, then the images do not change:

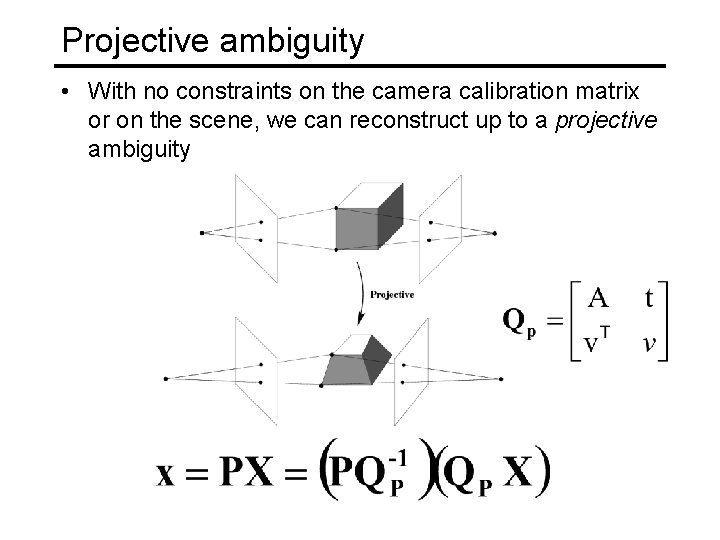
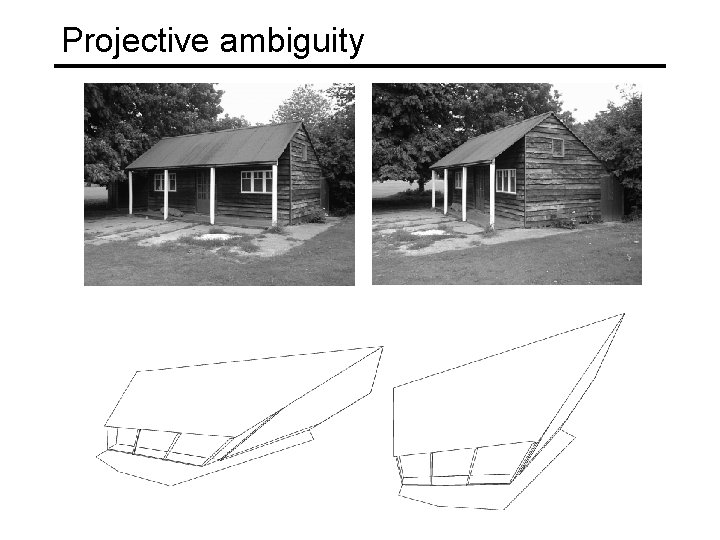
Projective ambiguity • With no constraints on the camera calibration matrix or on the scene, we can reconstruct up to a projective ambiguity

Projective ambiguity

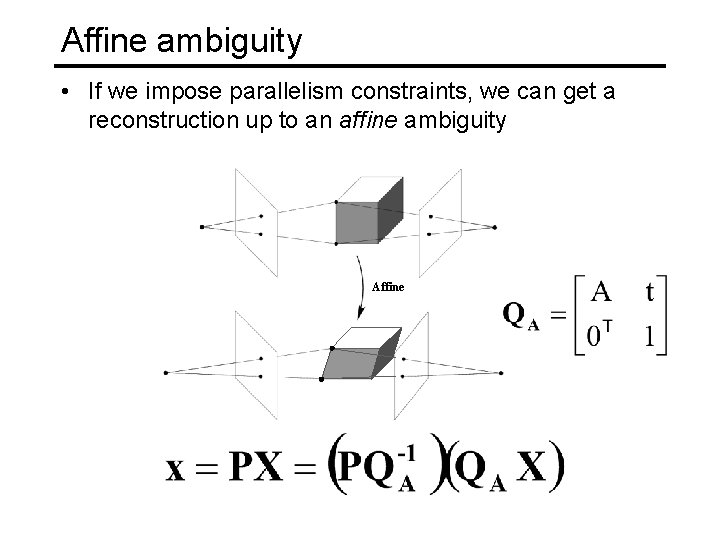
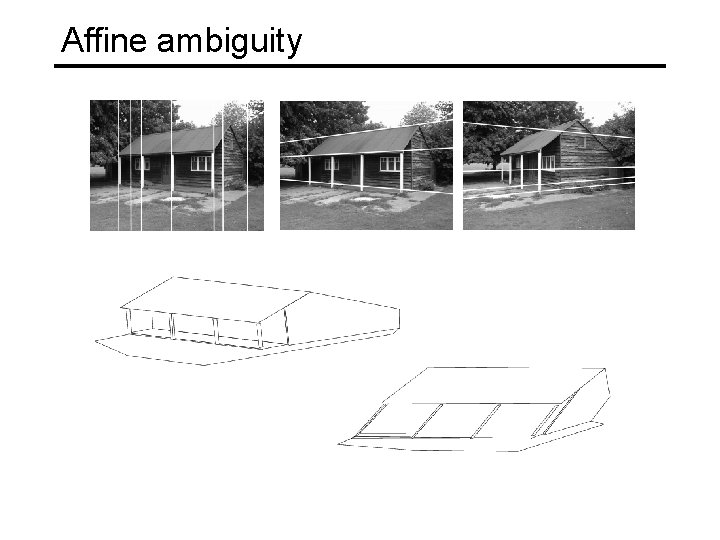
Affine ambiguity • If we impose parallelism constraints, we can get a reconstruction up to an affine ambiguity Affine

Affine ambiguity

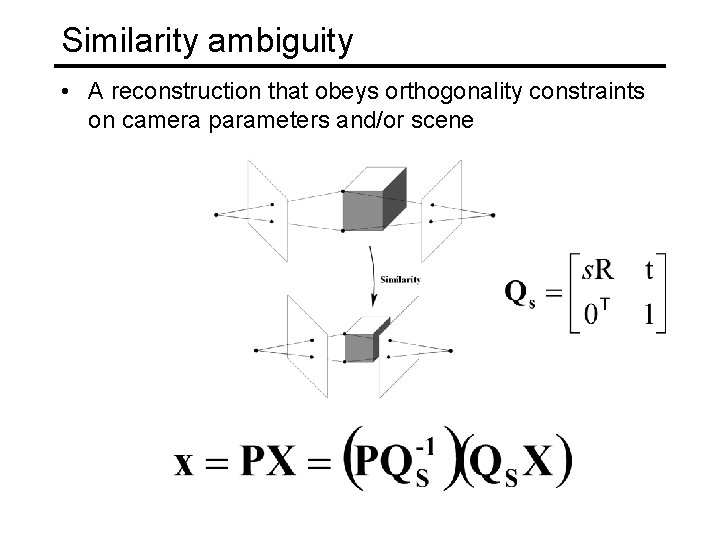
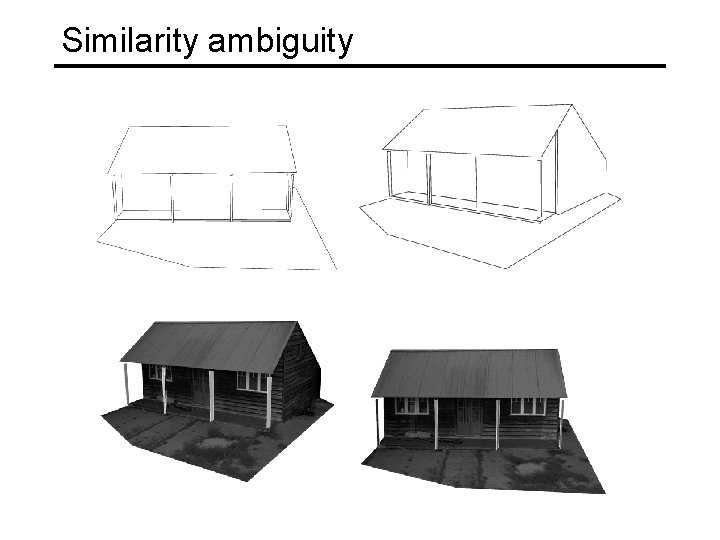
Similarity ambiguity • A reconstruction that obeys orthogonality constraints on camera parameters and/or scene

Similarity ambiguity

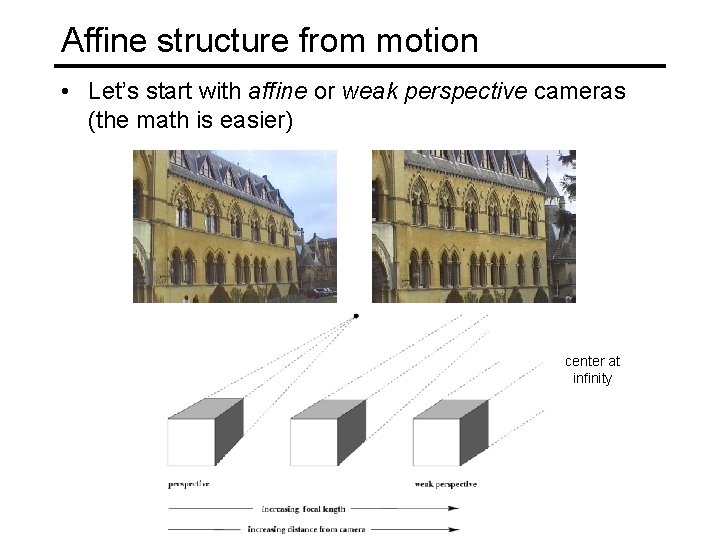
Affine structure from motion • Let’s start with affine or weak perspective cameras (the math is easier) center at infinity

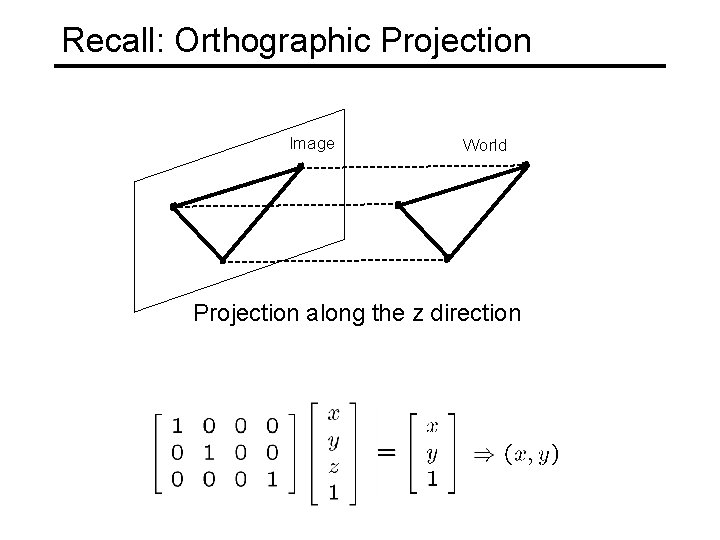
Recall: Orthographic Projection Image World Projection along the z direction

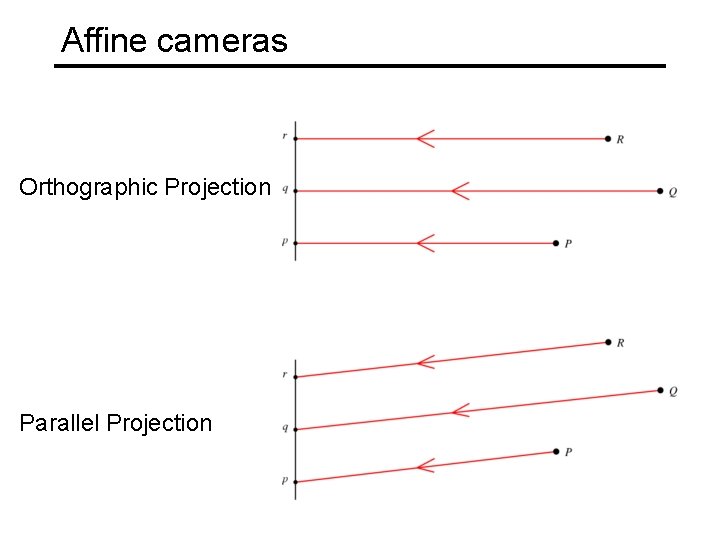
Affine cameras Orthographic Projection Parallel Projection

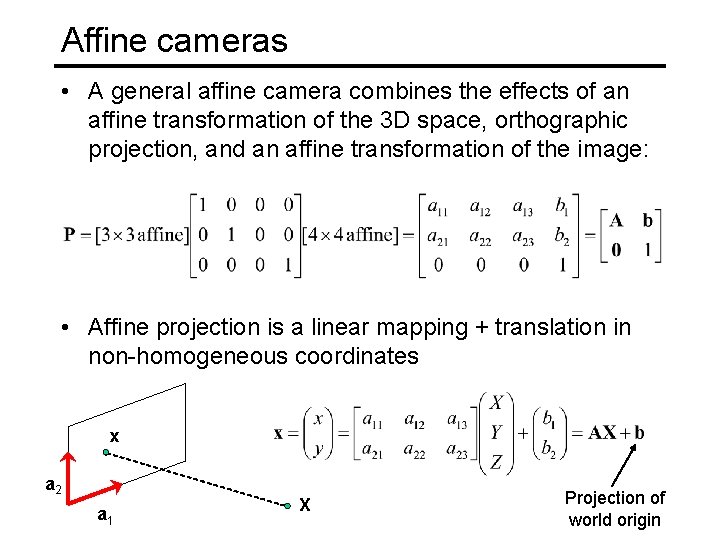
Affine cameras • A general affine camera combines the effects of an affine transformation of the 3 D space, orthographic projection, and an affine transformation of the image: • Affine projection is a linear mapping + translation in non-homogeneous coordinates x a 2 a 1 X Projection of world origin

Affine structure from motion • Given: m images of n fixed 3 D points: xij = Ai Xj + bi , i = 1, … , m, j = 1, … , n • Problem: use the mn correspondences xij to estimate m projection matrices Ai and translation vectors bi, and n points Xj • The reconstruction is defined up to an arbitrary affine transformation Q (12 degrees of freedom): • We have 2 mn knowns and 8 m + 3 n unknowns (minus 12 dof for affine ambiguity) • Thus, we must have 2 mn >= 8 m + 3 n – 12 • For two views, we need four point correspondences

Affine structure from motion • Centering: subtract the centroid of the image points in each view • For simplicity, set the origin of the world coordinate system to the centroid of the 3 D points • After centering, each normalized 2 D point is related to the 3 D point Xj by

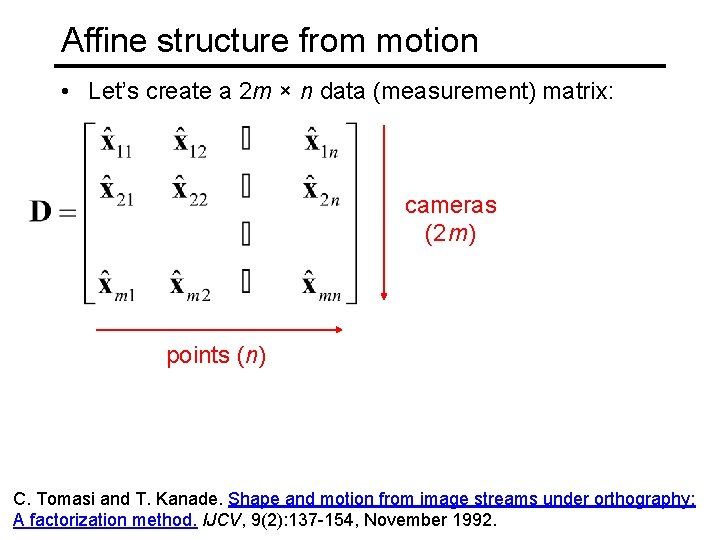
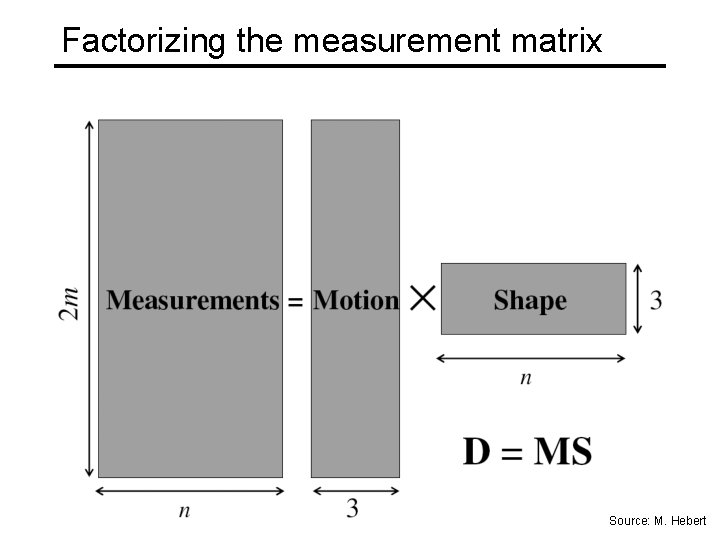
Affine structure from motion • Let’s create a 2 m × n data (measurement) matrix: cameras (2 m) points (n) C. Tomasi and T. Kanade. Shape and motion from image streams under orthography: A factorization method. IJCV, 9(2): 137 -154, November 1992.

Affine structure from motion • Let’s create a 2 m × n data (measurement) matrix: points (3 × n) cameras (2 m × 3) The measurement matrix D = MS must have rank 3! C. Tomasi and T. Kanade. Shape and motion from image streams under orthography: A factorization method. IJCV, 9(2): 137 -154, November 1992.

Factorizing the measurement matrix Source: M. Hebert

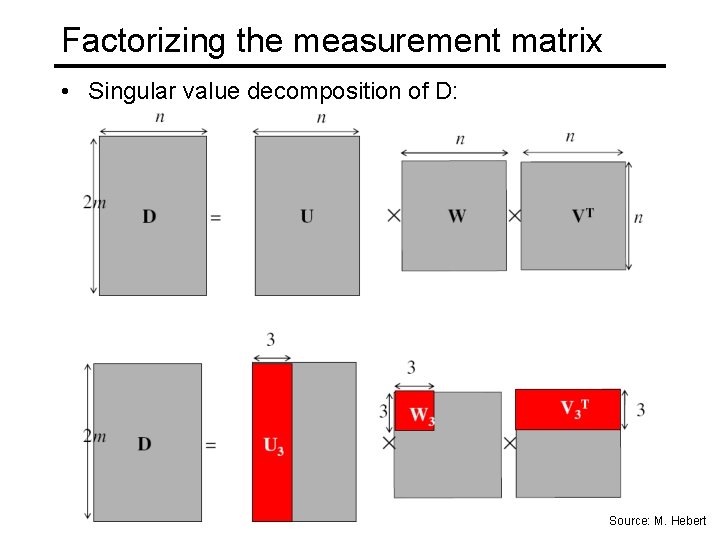
Factorizing the measurement matrix • Singular value decomposition of D: Source: M. Hebert

Factorizing the measurement matrix • Singular value decomposition of D: Source: M. Hebert

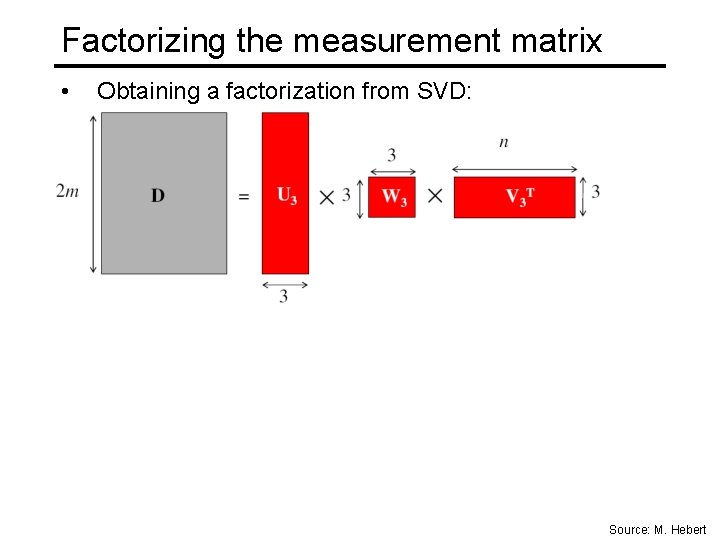
Factorizing the measurement matrix • Obtaining a factorization from SVD: Source: M. Hebert

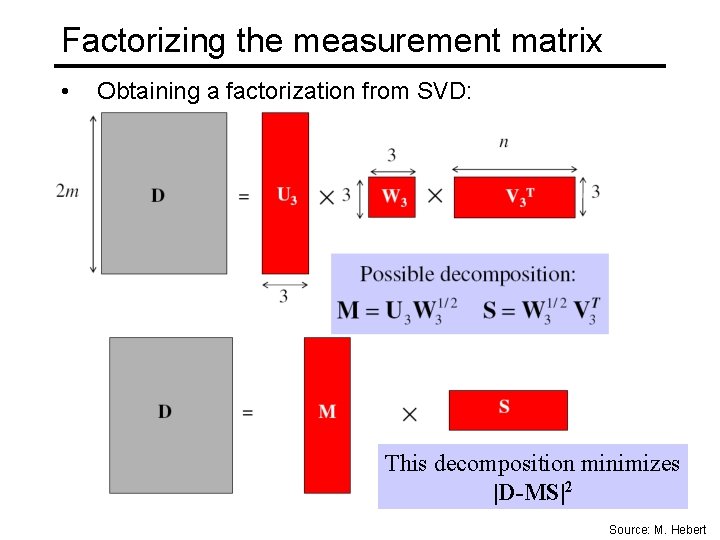
Factorizing the measurement matrix • Obtaining a factorization from SVD: This decomposition minimizes |D-MS|2 Source: M. Hebert

Affine ambiguity • The decomposition is not unique. We get the same D by using any 3× 3 matrix C and applying the transformations M → MC, S →C-1 S • That is because we have only an affine transformation and we have not enforced any Euclidean constraints (like forcing the image axes to be perpendicular, for example) Source: M. Hebert

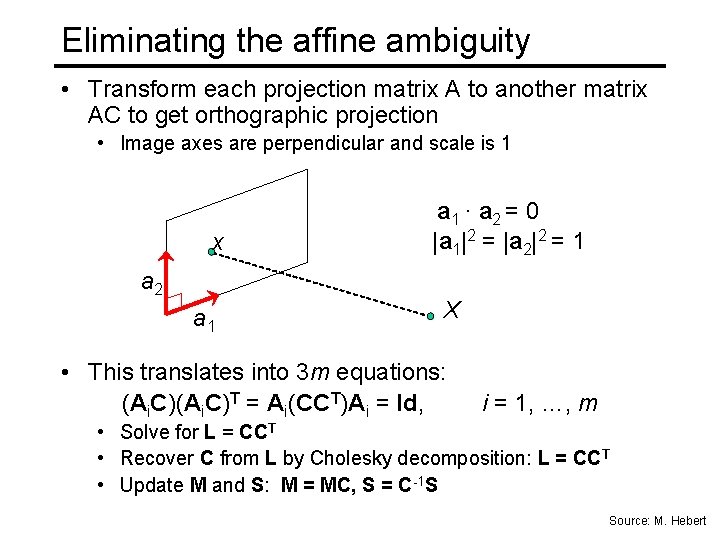
Eliminating the affine ambiguity • Transform each projection matrix A to another matrix AC to get orthographic projection • Image axes are perpendicular and scale is 1 x a 2 a 1 · a 2 = 0 |a 1|2 = |a 2|2 = 1 X • This translates into 3 m equations: (Ai. C)T = Ai(CCT)Ai = Id, i = 1, …, m • Solve for L = CCT • Recover C from L by Cholesky decomposition: L = CCT • Update M and S: M = MC, S = C-1 S Source: M. Hebert

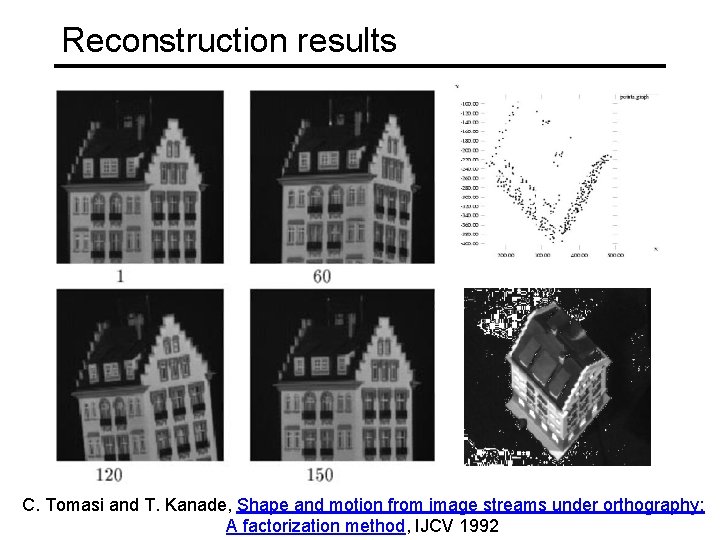
Reconstruction results C. Tomasi and T. Kanade, Shape and motion from image streams under orthography: A factorization method, IJCV 1992

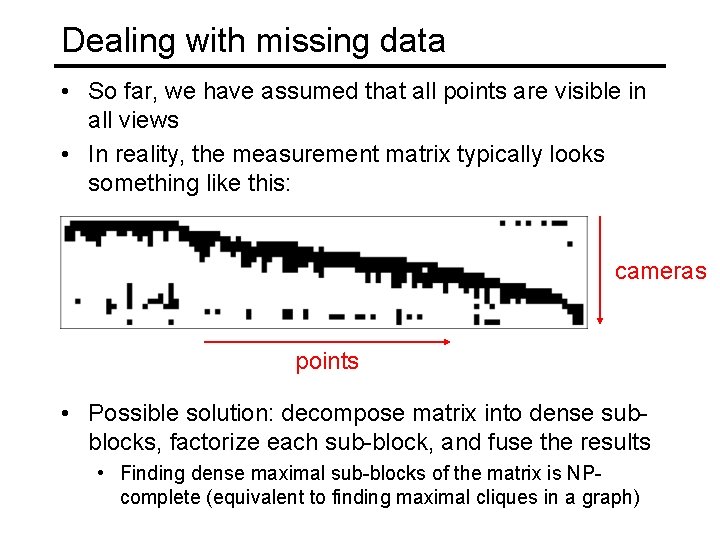
Dealing with missing data • So far, we have assumed that all points are visible in all views • In reality, the measurement matrix typically looks something like this: cameras points • Possible solution: decompose matrix into dense subblocks, factorize each sub-block, and fuse the results • Finding dense maximal sub-blocks of the matrix is NPcomplete (equivalent to finding maximal cliques in a graph)

Dealing with missing data • Incremental bilinear refinement (1) Perform factorization on a dense sub-block (2) Solve for a new 3 D point visible by at least two known cameras (triangulation) (3) Solve for a new camera that sees at least three known 3 D points (calibration) F. Rothganger, S. Lazebnik, C. Schmid, and J. Ponce. Segmenting, Modeling, and Matching Video Clips Containing Multiple Moving Objects. PAMI 2007.

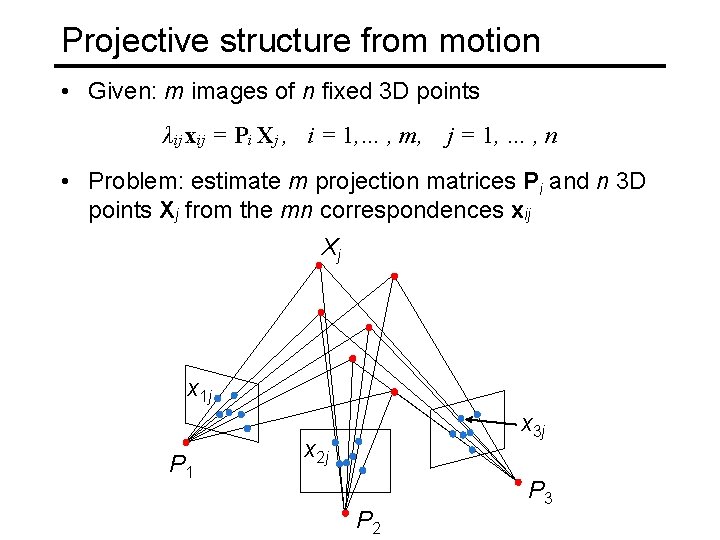
Projective structure from motion • Given: m images of n fixed 3 D points λij xij = Pi Xj , i = 1, … , m, j = 1, … , n • Problem: estimate m projection matrices Pi and n 3 D points Xj from the mn correspondences xij Xj x 1 j P 1 x 3 j x 2 j P 2 P 3

Projective structure from motion • Given: m images of n fixed 3 D points λij xij = Pi Xj , i = 1, … , m, j = 1, … , n • Problem: estimate m projection matrices Pi and n 3 D points Xj from the mn correspondences xij • With no calibration info, cameras and points can only be recovered up to a 4 x 4 projective transformation Q: X → QX, P → PQ-1 • We can solve for structure and motion when 2 mn >= 11 m +3 n – 15 • For two cameras, at least 7 points are needed

Projective SFM: Two-camera case • • Compute fundamental matrix F between the two views First camera matrix: [I | 0] Second camera matrix: [A | b] Then b is the epipole (FTb = 0), A = –[b×]F F&P sec. 8. 3. 2

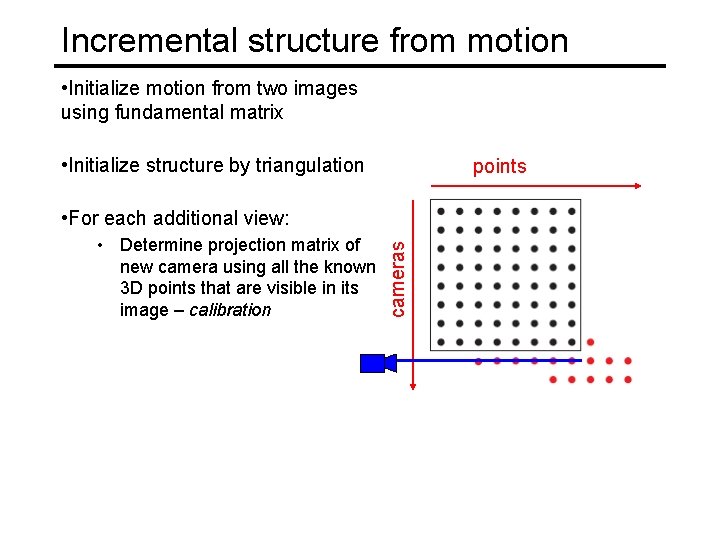
Incremental structure from motion • Initialize motion from two images using fundamental matrix • Initialize structure by triangulation points • Determine projection matrix of new camera using all the known 3 D points that are visible in its image – calibration cameras • For each additional view:

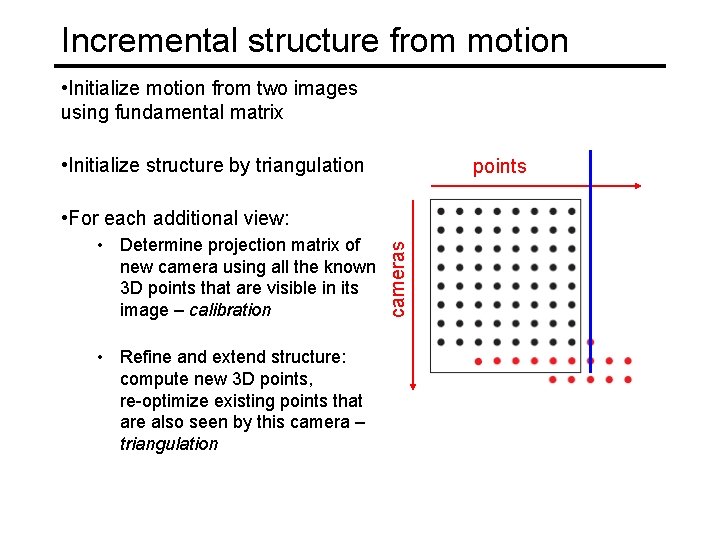
Incremental structure from motion • Initialize motion from two images using fundamental matrix • Initialize structure by triangulation points • Determine projection matrix of new camera using all the known 3 D points that are visible in its image – calibration • Refine and extend structure: compute new 3 D points, re-optimize existing points that are also seen by this camera – triangulation cameras • For each additional view:

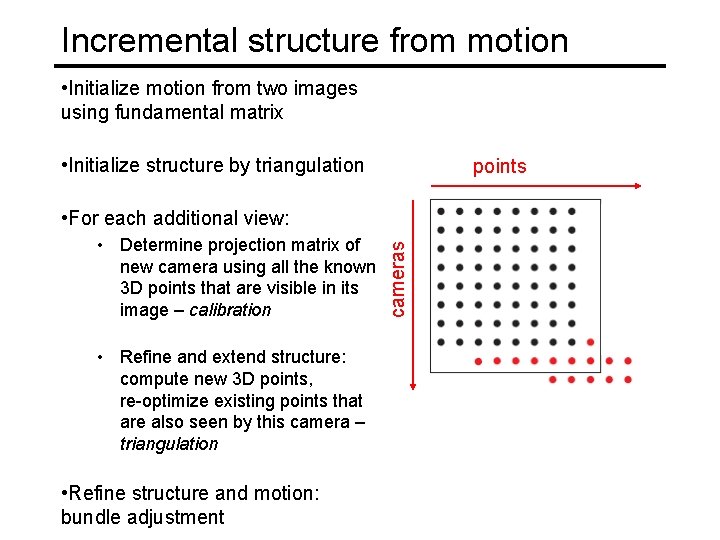
Incremental structure from motion • Initialize motion from two images using fundamental matrix • Initialize structure by triangulation points • Determine projection matrix of new camera using all the known 3 D points that are visible in its image – calibration • Refine and extend structure: compute new 3 D points, re-optimize existing points that are also seen by this camera – triangulation • Refine structure and motion: bundle adjustment cameras • For each additional view:

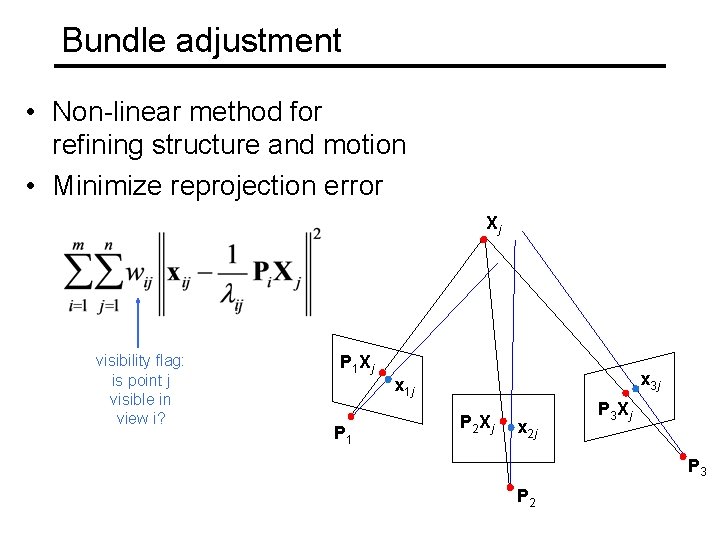
Bundle adjustment • Non-linear method for refining structure and motion • Minimize reprojection error Xj visibility flag: is point j visible in view i? P 1 Xj P 1 x 3 j x 1 j P 2 Xj x 2 j P 3 Xj P 3 P 2

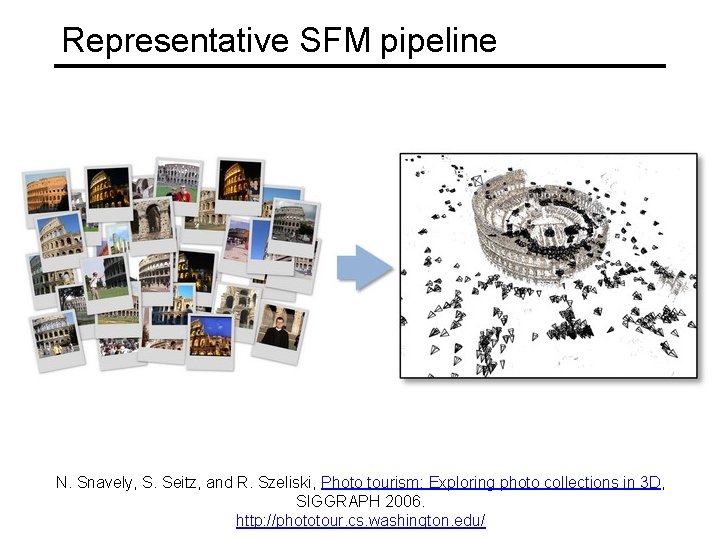
Representative SFM pipeline N. Snavely, S. Seitz, and R. Szeliski, Photo tourism: Exploring photo collections in 3 D, SIGGRAPH 2006. http: //phototour. cs. washington. edu/

Feature detection Detect SIFT features Source: N. Snavely

Feature detection Detect SIFT features Source: N. Snavely

Feature matching Match features between each pair of images Source: N. Snavely

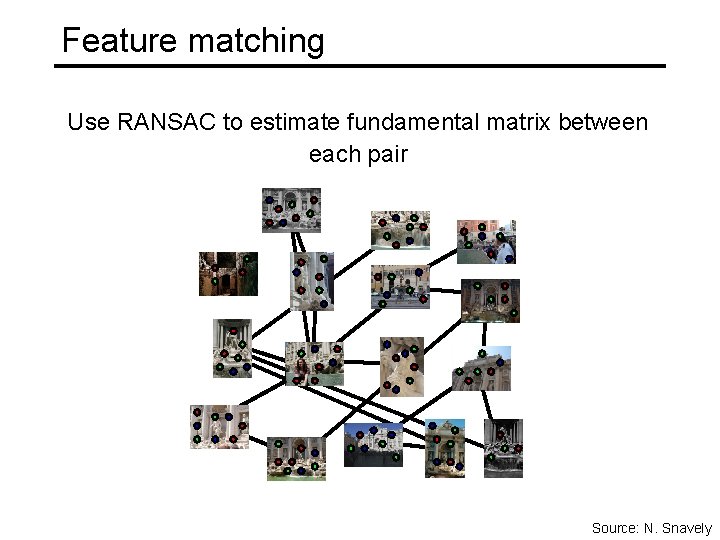
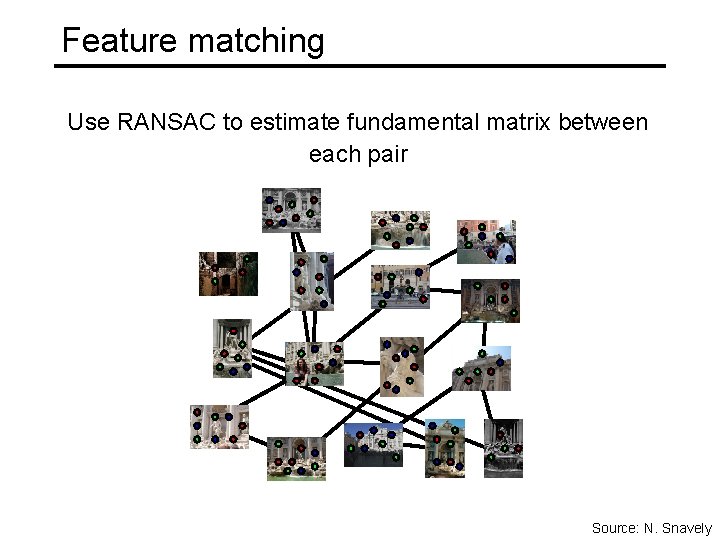
Feature matching Use RANSAC to estimate fundamental matrix between each pair Source: N. Snavely

Feature matching Use RANSAC to estimate fundamental matrix between each pair Image source

Feature matching Use RANSAC to estimate fundamental matrix between each pair Source: N. Snavely

Image connectivity graph (graph layout produced using the Graphviz toolkit: http: //www. graphviz. org/) Source: N. Snavely

Incremental SFM • Pick a pair of images with lots of inliers (and preferably, good EXIF data) • Initialize intrinsic parameters (focal length, principal point) from EXIF • Estimate extrinsic parameters (R and t) using five-point algorithm • Use triangulation to initialize model points • While remaining images exist • Find an image with many feature matches with images in the model • Run RANSAC on feature matches to register new image to model • Triangulate new points • Perform bundle adjustment to re-optimize everything

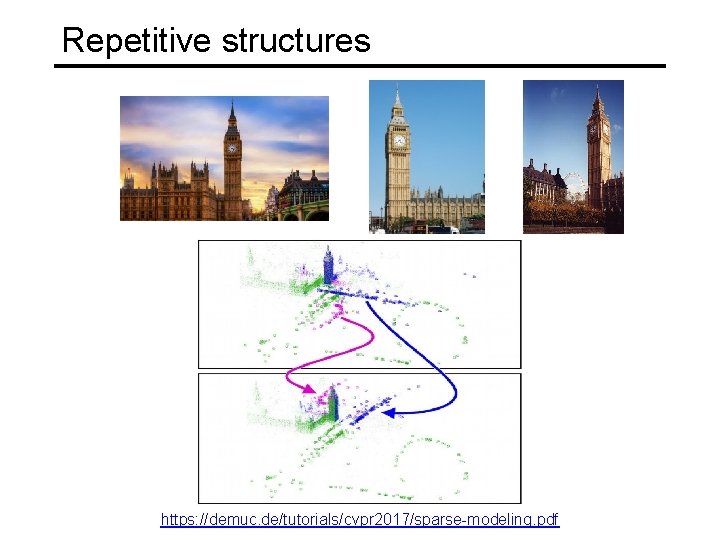
The devil is in the details • Handling degenerate configurations (e. g. , homographies) • Eliminating outliers • Dealing with repetitions and symmetries

Repetitive structures https: //demuc. de/tutorials/cvpr 2017/sparse-modeling. pdf

The devil is in the details • • • Handling degenerate configurations (e. g. , homographies) Eliminating outliers Dealing with repetitions and symmetries Handling multiple connected components Closing loops Making the whole thing efficient! • See, e. g. , Towards Linear-Time Incremental Structure from Motion

SFM software • • • Bundler Open. Sf. M Open. MVG Visual. SFM See also Wikipedia’s list of toolboxes

Review: Structure from motion • Ambiguity • Affine structure from motion • Factorization • Dealing with missing data • Incremental structure from motion • Projective structure from motion • Bundle adjustment • Modern structure from motion pipeline
 Passive rom vs active rom
Passive rom vs active rom Simple harmonic motion equations
Simple harmonic motion equations An object in motion stays in motion
An object in motion stays in motion Chapter 2 section 1 describing motion answer key
Chapter 2 section 1 describing motion answer key Measuring motion
Measuring motion Section 1 describing motion worksheet answer key
Section 1 describing motion worksheet answer key Describing motion chapter 1 lesson 1
Describing motion chapter 1 lesson 1 Motion section 1 describing motion
Motion section 1 describing motion Structure from motion
Structure from motion Structure from motion
Structure from motion Conclusion of yashpal committee report
Conclusion of yashpal committee report Writing linear equations given two points
Writing linear equations given two points The exclusive legal right given to an originator
The exclusive legal right given to an originator Indicators of past perfect tense
Indicators of past perfect tense Given that venn diagram
Given that venn diagram Partitioning a line segment formula
Partitioning a line segment formula Lesson 2 reflections answer key
Lesson 2 reflections answer key Dental formula for deciduous teeth
Dental formula for deciduous teeth Theory of status withdrawal related to
Theory of status withdrawal related to Variational principle
Variational principle Functionalist theory definition
Functionalist theory definition Strain energy due to axial load
Strain energy due to axial load Irrelevant sentence adalah
Irrelevant sentence adalah Simple interest formula
Simple interest formula Structural functional analysis is given by
Structural functional analysis is given by Position vector definition
Position vector definition Metasploit gui kali
Metasploit gui kali Fill past perfect
Fill past perfect All squares are rhombuses
All squares are rhombuses A line pq 100 mm long is inclined at 30
A line pq 100 mm long is inclined at 30 All evil begins with 15 volts
All evil begins with 15 volts P(a and b) formula
P(a and b) formula Subdividing a segment in a given ratio
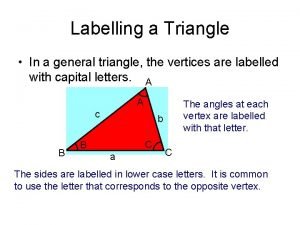
Subdividing a segment in a given ratio Labelling a triangle
Labelling a triangle The hamiltonian operator is given by
The hamiltonian operator is given by Which rating star is given by griha for points 71-80
Which rating star is given by griha for points 71-80 Lesson 5-6 inequalities in two triangles answer key
Lesson 5-6 inequalities in two triangles answer key It is an immediate and temporary care given to a person
It is an immediate and temporary care given to a person Finding a missing endpoint
Finding a missing endpoint Fill in each blank with a or an
Fill in each blank with a or an Wavelength frequency equation
Wavelength frequency equation How to find inscribed angle
How to find inscribed angle Dmv triangle chemistry
Dmv triangle chemistry Cimah regulation
Cimah regulation Police report that 78 of drivers are given a breath test
Police report that 78 of drivers are given a breath test Site:slidetodoc.com
Site:slidetodoc.com When is a walkout receipt given to the patient?
When is a walkout receipt given to the patient? A given b probability
A given b probability Inequality
Inequality Formula for calculating average atomic mass
Formula for calculating average atomic mass Brainstorming method of teaching examples
Brainstorming method of teaching examples All both neither none either
All both neither none either Indivisibility in production function
Indivisibility in production function Pa(b)
Pa(b)