Strain Energy Due to Shear Bending and Torsion

Strain Energy Due to Shear, Bending and Torsion Lecture No-6 J P Supale Mechanical Engineering Department SKN SITS LONAVALA Strength of Materials

Strain Energy due to Shear Consider a cube ABCD of side L being subjected to a shear force P which is applied tangentially to the side CD. As a result, side CD changes to C’D’. D δl D’ Φ P C’ C Φ L A B Let Φ=Angle turned by the side AD as a result of P being applied τ=Shear stress induced on the side CD A= Area of each side=Lx. L G=Modulus of rigidity of the material of cube Strength of Materials

Strain Energy due to Shear The shear force P is given as In ADD’ When Φ is very small Strength of Materials

Strain Energy due to Shear Work done by shear force is given as As we know, work done =strain energy stored in the cube, is given as Where V=Lx. L= Volume of cube Strength of Materials

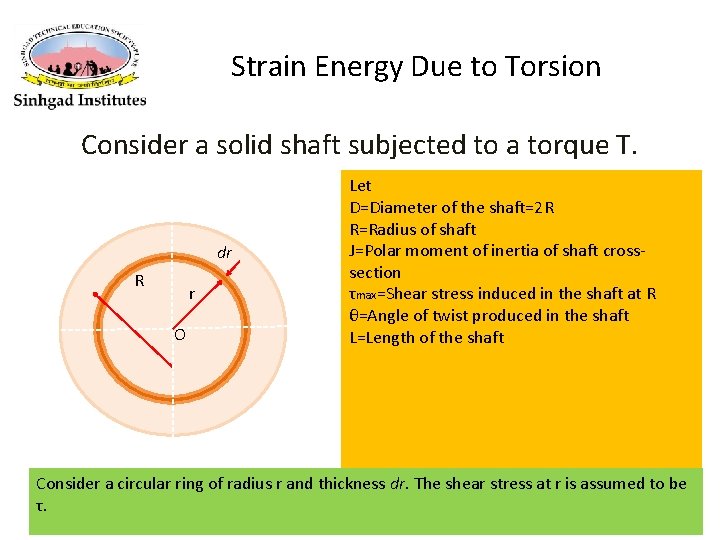
Strain Energy Due to Torsion Consider a solid shaft subjected to a torque T. dr R r O Let D=Diameter of the shaft=2 R R=Radius of shaft J=Polar moment of inertia of shaft crosssection τmax=Shear stress induced in the shaft at R θ=Angle of twist produced in the shaft L=Length of the shaft Consider a circular ring of radius r and thickness dr. The shear stress at r is assumed to be τ. Strength of Materials

Strain Energy Due to Torsion Strain energy stored in the ring is given as Total strain energy stored in the shaft is obtained as From torsion equation, we have Strength of Materials

Strain Energy Due to Torsion Equation 22 on substituting τ becomes, Strength of Materials

Strain Energy Due to Torsion If solid shaft is replaced by a hollow shaft of outside diameter Do and inside diameter Di, then equation 23 changes to Volume of hollow shaft is given as Strength of Materials

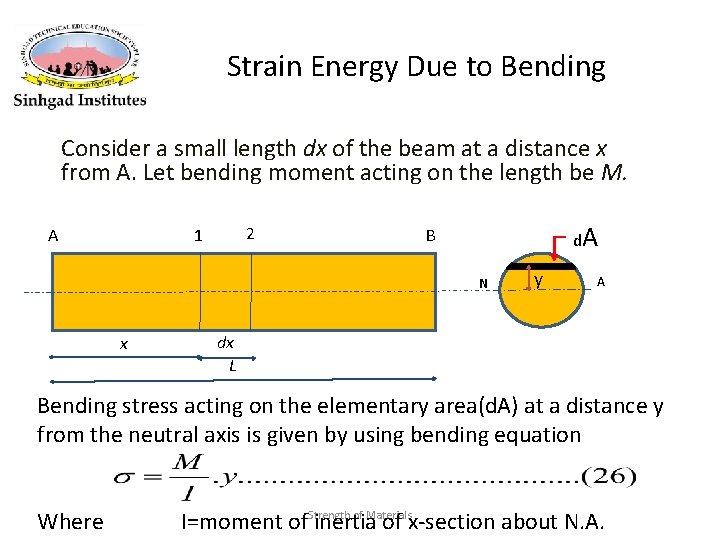
Strain Energy Due to Bending Consider a small length dx of the beam at a distance x from A. Let bending moment acting on the length be M. 2 1 A d. A B N x y A dx L Bending stress acting on the elementary area(d. A) at a distance y from the neutral axis is given by using bending equation Where of Materials I=moment of. Strength inertia of x-section about N. A.

Strain Energy Due to Bending Strain energy stored in the elementary area is Strain energy stored in the beam between 1 and 2 is given as Strength of Materials

Strain Energy Due to Bending Strain energy stored in the entire beam is obtained as Strength of Materials

Numerical 1 1. A cantilever beam of span 2 m having cross section 30 mm wide by 75 mm deep. Determine strain energy stored in beam if Concentrated load of 1. 75 k. N act at free end. Take E=200 GPa L=2 m d= 75 mm =0. 075 mm Strength of Materials b=30 mm= 0. 03 m E=200 x 109 N/m 2

• Moment of Inertia • Flexural Rigidity, EI Strength of Materials

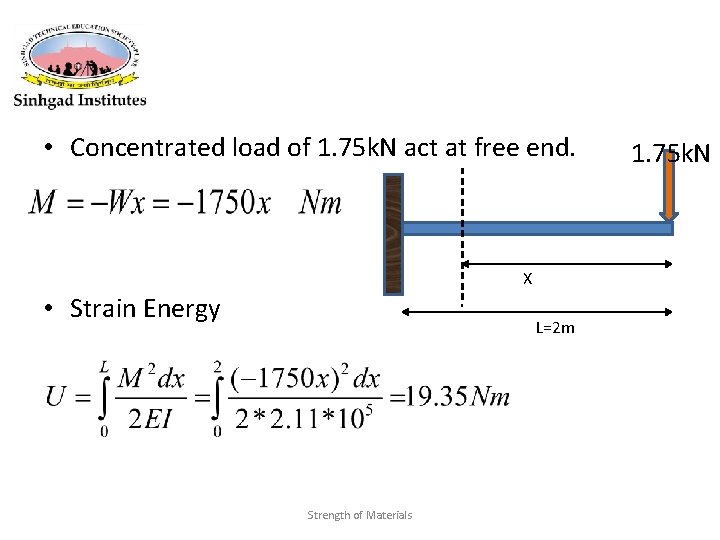
• Concentrated load of 1. 75 k. N act at free end. X • Strain Energy L=2 m Strength of Materials 1. 75 k. N

Numerical 2 • A cantilever beam of span 2 m having cross section 30 mm wide by 75 mm deep. Determine strain energy stored in beam if total 2 k. N load is uniformly spread over entire span • Take E=200 Gpa L=2 m b=30 mm= 0. 03 m d= 75 mm =0. 075 mm E=200 x 109 N/m 2 Strength of Materials

• Moment of Inertia • Flexural Rigidity, EI Strength of Materials

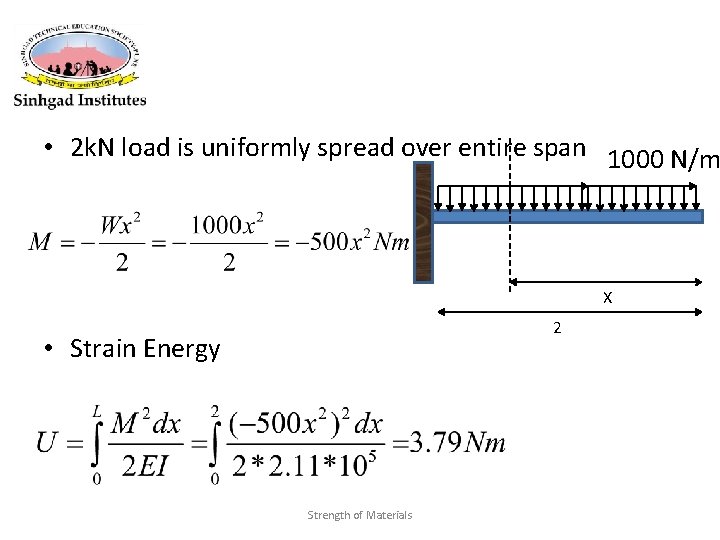
• 2 k. N load is uniformly spread over entire span 1000 N/m X 2 • Strain Energy Strength of Materials

Workout Numerical 1 • Find an expression for strain energy due to bending for a SSB of span L, the beam carrying UDL w per unit run over whole span. Draw beam diagram. Calculate Reactions. Apply Macaulays method, to get Put this bending moment in strain energy equation Strength of Materials

Workout Numerical 1 • A beam 6 m in length is carrying UDL of 10 k. N/m length. Determine the strain energy stored in the beam. Take E 200 GPa and I=1500 cm 4. Draw diagram of loading, calculate reactions. Apply Macaulays method to get moment equation as Put this bending moment in strain energy equation Strength of Materials