SCOMPOSIZIONI Definizione Scomporre in fattori significa scrivere un

SCOMPOSIZIONI

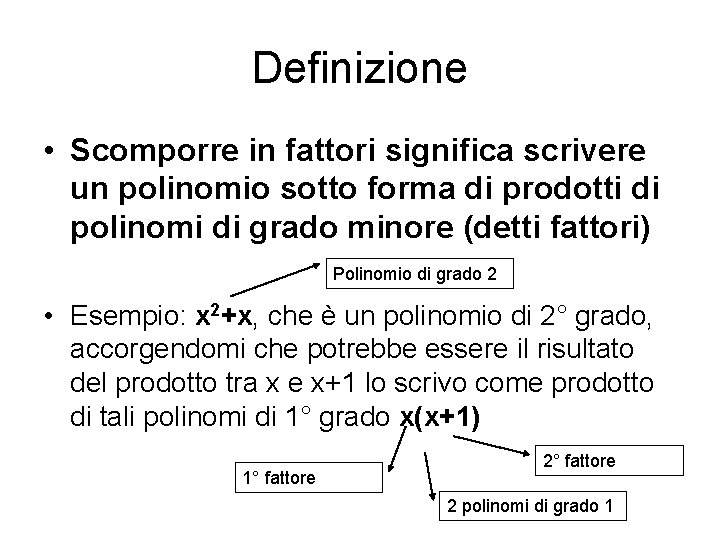
Definizione • Scomporre in fattori significa scrivere un polinomio sotto forma di prodotti di polinomi di grado minore (detti fattori) Polinomio di grado 2 • Esempio: x 2+x, che è un polinomio di 2° grado, accorgendomi che potrebbe essere il risultato del prodotto tra x e x+1 lo scrivo come prodotto di tali polinomi di 1° grado x(x+1) 1° fattore 2 polinomi di grado 1

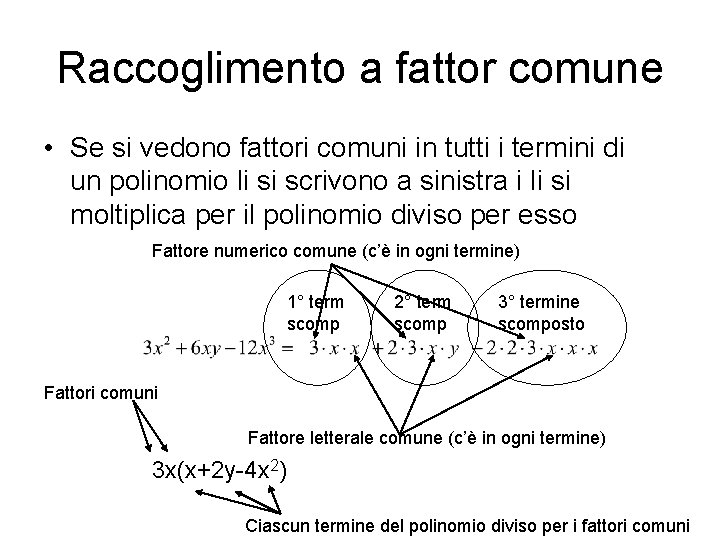
Raccoglimento a fattor comune • Se si vedono fattori comuni in tutti i termini di un polinomio li si scrivono a sinistra i li si moltiplica per il polinomio diviso per esso Fattore numerico comune (c’è in ogni termine) 1° term scomp 2° term scomp 3° termine scomposto Fattori comuni Fattore letterale comune (c’è in ogni termine) 3 x(x+2 y-4 x 2) Ciascun termine del polinomio diviso per i fattori comuni

Raccoglimento di polinomi comuni • Se una espressione contiene come fattori dei polinomi comuni a tutti i termini si può operare il raccoglimento di tali polinomi. • Esempio: (3 x+5)x-(3 x+5)y equivale a (3 x+5)(x-y)

Raccoglimento a fattor comune parziale • Se si vedono fattori comuni ad un gruppo di termini (anche non vicini) e altri fattori comuni ad altri termini in modo da intuire che alcuni polinomi ridotti che si ottengono sono uguali, si procede con i 2 raccoglimenti parziali e quindi si raccoglie il polinomio fattore • Esempio 4 xb-ay-4 yb+ax noto che se raccolgo dal 1° e 3° termine 4 b ottengo 4 b(x-y) se raccolgo dal 4° e 2° termine a ottengo a(x-y) da 4 b(x-y)+a(x-y) posso raccogliere il fattore (x-y) ottenendo (x-y)(4 b+a)

Regole inverse dei prodotti notevoli trinomio derivante dal quadrato di un binomio • Notando che un trinomio è formato da 2 quadrati positivi a cui è sommato o sottratto il doppio prodotto delle basi dei quadrati si può trasformare il trinomio nel quadrato delle somma o differenza delle basi. • Esempio In 25 x 2 -10 x+1 si può riconoscere 2 quadrati (di 5 x e di 1) e la sottrazione del doppio prodotto tra 5 x e 1 per cui si può scrivere =(5 x -1)2

Regole inverse dei prodotti notevoli quadrinomio derivante da cubo d’un binomio • Notando che un quadrinomio è formato da 2 cubi a cui sono sommati o sottratti i 2 tripli prodotti di una base al quadrato per l’altra si può trasformare il quadrinomio nel cubo della somma o differenza delle basi. • Esempio In 8 x 3+12 x 2 y – 6 xy 2 -y 3 si può riconoscere 2 cubi (di 2 x e di -y) e e i 2 tripli prodotti tra (2 x)2 e -y e 2 x e (-y)2 per cui si può scrivere =(2 x-y)3

Regole inverse dei prodotti notevoli binomio derivante dalla somma di 2 monomi per la loro differenza • Notando che un binomio è formato da 2 quadrati di segno opposto si può trasformare il binomio nel prodotto della somma delle 2 basi per la loro differenza. • Esempio In 4 x 2–y 2 si può riconoscere 2 quadrati (di 2 x e di y) per cui si può scrivere =(2 x+y)(2 x-y)

Regole inverse dei prodotti notevoli binomio corrispondente alla somma o differenza tra 2 cubi • Notando che un binomio è formato da 2 cubi sommati o sottratti tra loro si può trasformare il binomio nel prodotto della somma o differenza delle 2 basi per il falso quadrato della loro differenza o somma. • Esempio in 27 x 3–y 3 si può riconoscere 2 cubi (di 3 x e di y) per cui si può scrivere =(3 x-y)(9 x 2 +3 xy+y 2 )

Regole inverse dei prodotti notevoli polinomio di 6 termini di cui 3 quadrati e 3 doppi prodotti tra le loro basi • Notando che polinomio è formato da 3 quadrati positivi e da 3 doppi prodotti delle loro basi lo si può trasformare nel quadrato della somma o differenza delle 3 basi. • Esempio in x 2+4 y 2+49 z 2 -4 xy+14 xz-28 yz si può riconoscere 3 quadrati (di x, 2 y e 7 z e 3 doppi prodotti 2 x(-2 y), 2 x(7 z), (-2 y)(7 z) per cui si può scrivere =(x-2 y+7 z)2

Trinomio del tipo x 2+sx+p • Notando un trinomio formato da un quadrato con coefficiente =1 se riconosciamo che esistono 2 numeri a e b il cui prodotto è = al termine noto e la cui somma = al coefficiente del termine di 1° grado allora possiamo scomporre il trinomio come (x+a)(x+b). • Esempio in x 2+6 x+8 si può riconoscere che 8 è 2 per 4 e 6 2 più 4 per cui =(x+2)(x+4)

Scomposizione con Ruffini • Se non troviamo altri metodi si può cercare di vedere se il polinomio è divisibile per xa: la regola di Ruffini ci garantisce che un polinomio è divisibile per x-a se sostituendo il valore di a alla x si ottiene una identità