ROTATIONAL MOTION CHAPTER 8 Types of Motion There

ROTATIONAL MOTION CHAPTER 8

Types of Motion There are 2 types of pure unmixed motion: Translational - linear motion Rotational - motion involving a rotation or revolution around a fixed chosen axis( an axis which does not move). We need a system that defines BOTH types of motion working together on a system. Rotational quantities are usually defined with units involving a radian measure.

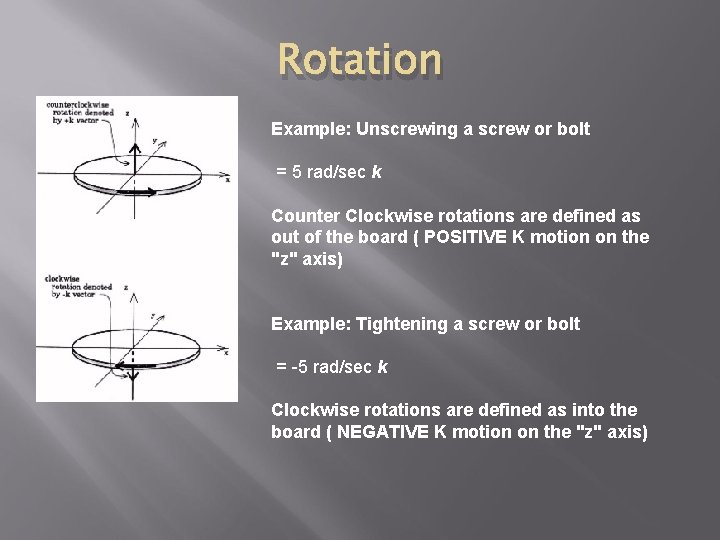
Rotation Example: Unscrewing a screw or bolt = 5 rad/sec k Counter Clockwise rotations are defined as out of the board ( POSITIVE K motion on the "z" axis) Example: Tightening a screw or bolt = -5 rad/sec k Clockwise rotations are defined as into the board ( NEGATIVE K motion on the "z" axis)

Angular Displacement 1. 2. 3. Circular motion about AXIS Three different measures of angles: Degrees Revolutions (1 rev. = 360 deg. ) Radians (2 p rads = 360 deg. )

Example An automobile wheel has a radius of 42 cm. If a car drives 10 km, through what angle has the wheel rotated? a) In revolutions b) In radians c) In degrees

Angular Speed Can be given in Revolutions/s Radians/s --> Called w Degrees/s Linear Speed at r

Example A race car engine can turn at a maximum rate of 12 000 rpm. (revolutions per minute). a) What is the angular velocity in radians per second. b) If helipcopter blades were attached to the crankshaft while it turns with this angular velocity, what is the maximum radius of a blade such that the speed of the blade tips stays below the speed of sound. DATA: The speed of sound is 343 m/s

Angular Velocity Since velocity is defined as the rate of change of displacement. ANGULAR VELOCITY is defined as the rate of change of ANGULAR DISPLACEMENT. NOTE: Translational motion tells you TWO THINGS • magnitude of the motion and the units • • direction on the given axis Example: v =3 m/s This tells us that the magnitude is 3 m/s, the positive axis direction

Angular Acceleration Denoted by a w must be in radians per sec. Units of angular acceleration are rad/s² Every portion of the object has same angular speed and same angular acceleration

Angular Acceleration Once again, following the same lines of logic. Since acceleration is defined as the rate of change of velocity. We can say the ANGULAR ACCELERATION is defined as the rate of change of the angular velocity. Also, we can say that the ANGULAR ACCELERATION is the TIME DERIVATIVE OF THE ANGULAR VELOCITY. All the rules for integration apply as well.

Linear movement of a rotating point Distance Speed Acceleration Different points on the same object have different linear motions! Only works when q, w and are in radians!

Analogies Between Linear and Rotational Motion Linear Motion

Example A pottery wheel is accelerated uniformly from rest to a rate of 10 rpm in 30 seconds. a. ) What was the angular acceleration? (in rad/s 2) b. )How many revolutions did the wheel undergo during that time?

Example A coin of radius 1. 5 cm is initially rolling with a rotational speed of 3. 0 radians per second, and comes to a rest after experiencing a slowing down of a = 0. 05 rad/s 2. a. ) Over what angle (in radians) did the coin rotate? b. ) What linear distance did the coin move?

Example A turntable capable of angularly accelerating at 12 rad/s 2 needs to be given an initial angular velocity if it is to rotate through a net 400 radians in 6 seconds. What must its initial angular velocity be? 30. 7 rad/s

Center of Mass Note that weight doesn’t act at a single point – it is distributed over the entire body However, we can always calculate the torque due to a body’s weight by assuming that the entire force of gravity (weight) is concentrated at a single point called the center of gravity If the acceleration of gravity has the same value at all points on a body, its center of gravity is identical to its center of mass (where all mass of object is considered concentrated at a single point)

Center of Mass m 2 m 1 m 3 For a system of point particles: The center of mass of the system is the point in space having coordinates (x. CM, y. CM) defined by: Average position of set of particles, weighted by their masses Coordinates where all the mass of entire system can be considered to be concentrated

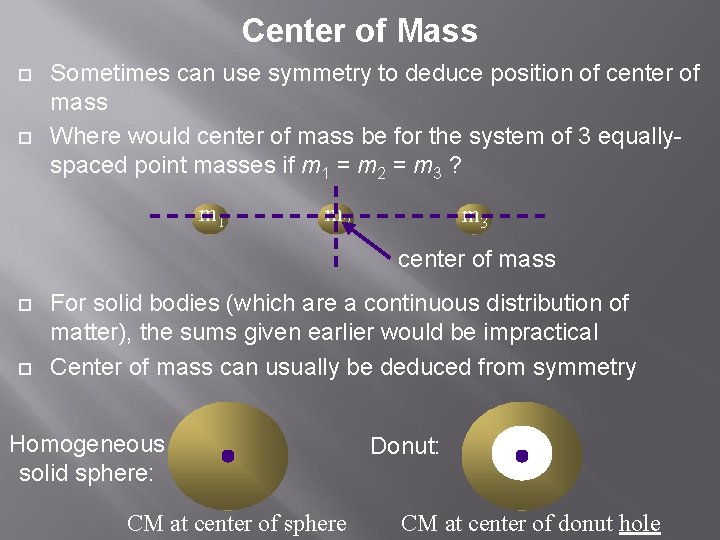
Center of Mass Sometimes can use symmetry to deduce position of center of mass Where would center of mass be for the system of 3 equallyspaced point masses if m 1 = m 2 = m 3 ? m 1 m 2 m 3 center of mass For solid bodies (which are a continuous distribution of matter), the sums given earlier would be impractical Center of mass can usually be deduced from symmetry Homogeneous solid sphere: CM at center of sphere Donut: CM at center of donut hole

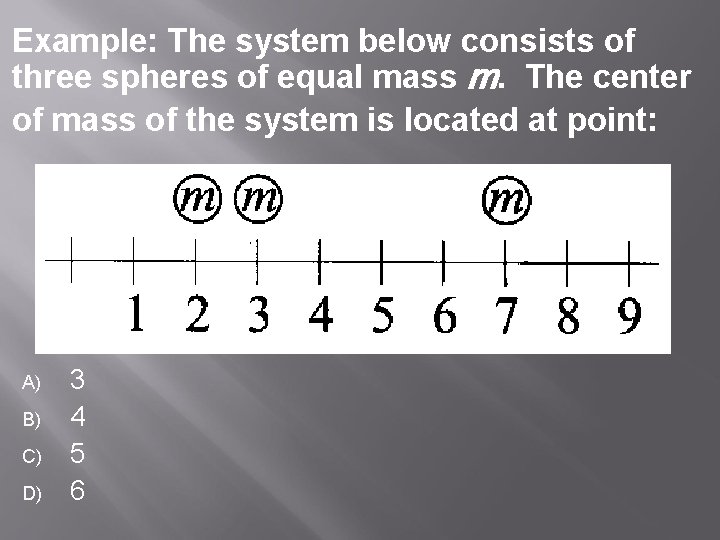
Example: The system below consists of three spheres of equal mass m. The center of mass of the system is located at point: A) B) C) D) 3 4 5 6

Rotational Kinetic Energy and Inertia Just like massive bodies tend to resist changes in their motion ( AKA - "Inertia"). Rotating bodies also tend to resist changes in their motion. We call this ROTATIONAL INERTIA. We can determine its expression by looking at Kinetic Energy. We now have an expression for the rotation of a mass in terms of the radius of rotation. We call this quantity the MOMENT OF INERTIA (I) with units kgm 2

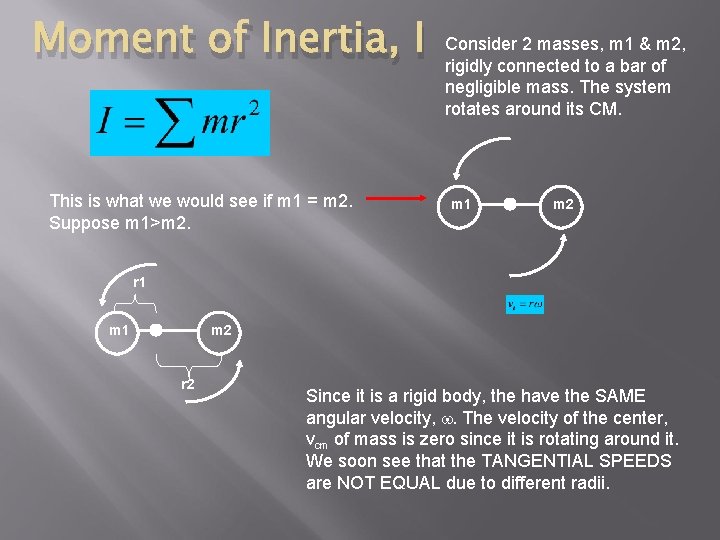
Moment of Inertia, I This is what we would see if m 1 = m 2. Suppose m 1>m 2. Consider 2 masses, m 1 & m 2, rigidly connected to a bar of negligible mass. The system rotates around its CM. m 1 m 2 r 2 Since it is a rigid body, the have the SAME angular velocity, w. The velocity of the center, vcm of mass is zero since it is rotating around it. We soon see that the TANGENTIAL SPEEDS are NOT EQUAL due to different radii.

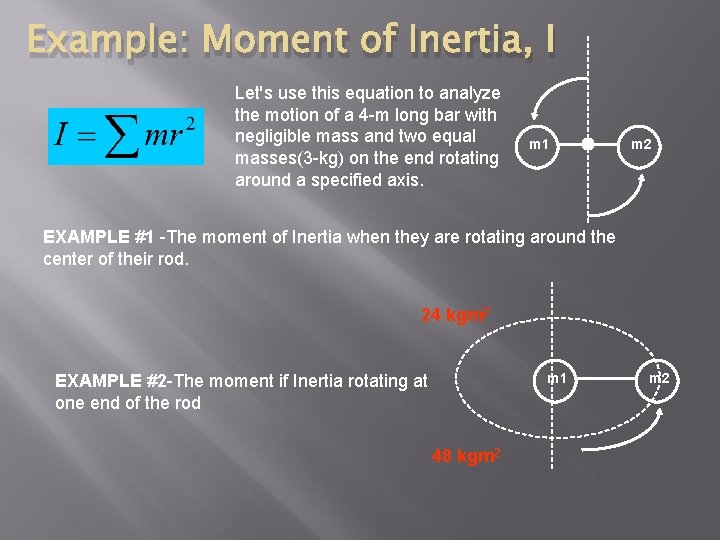
Example: Moment of Inertia, I Let's use this equation to analyze the motion of a 4 -m long bar with negligible mass and two equal masses(3 -kg) on the end rotating around a specified axis. m 1 m 2 EXAMPLE #1 -The moment of Inertia when they are rotating around the center of their rod. 24 kgm 2 m 1 EXAMPLE #2 -The moment if Inertia rotating at one end of the rod 48 kgm 2

Example cont’ Now let’s calculate the moment of Inertia rotating at a point 2 meters from one end of the rod. m 1 m 2 2 m 120 kgm 2 As you can see, the FARTHER the axis of rotation is from the center of mass, the moment of inertia increases. We need an expression that will help us determine the moment of inertia when this situation arises.

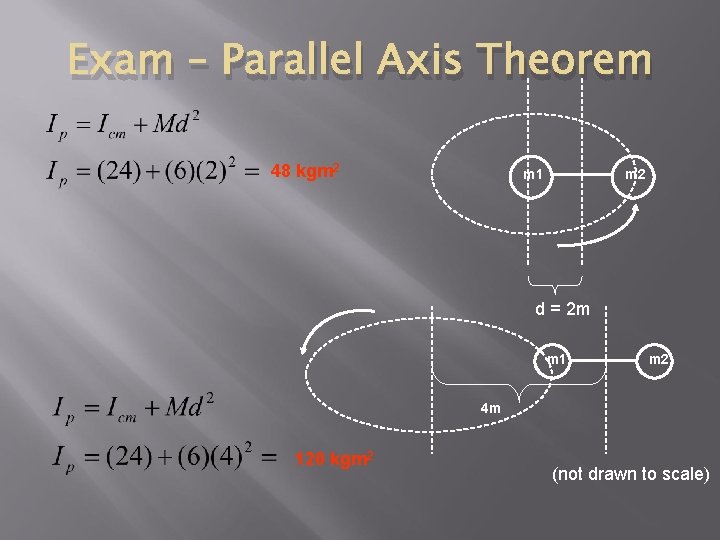
Parallel Axis Theorem This theorem will allow us to calculate the moment of inertia of any rotating body around any axis, provided we know the moment of inertia about the center of mass. It basically states that the Moment of Inertia ( Ip) around any axis "P" is equal to the known moment of inertia (Icm) about some center of mass plus M ( the total mass of the system) times the square of "d" ( the distance between the two parallel axes) Using the prior example let’s use the parallel axis theorem to calculate the moment of inertia when it is rotating around one end and 2 m from a fixed axis.

Exam – Parallel Axis Theorem 48 kgm 2 m 1 m 2 d = 2 m m 1 m 2 4 m 120 kgm 2 (not drawn to scale)

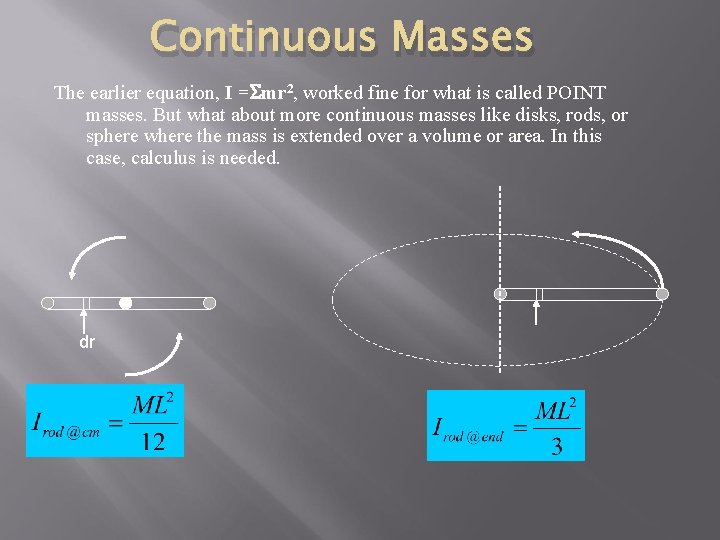
Continuous Masses The earlier equation, I = mr 2, worked fine for what is called POINT masses. But what about more continuous masses like disks, rods, or sphere where the mass is extended over a volume or area. In this case, calculus is needed. dr

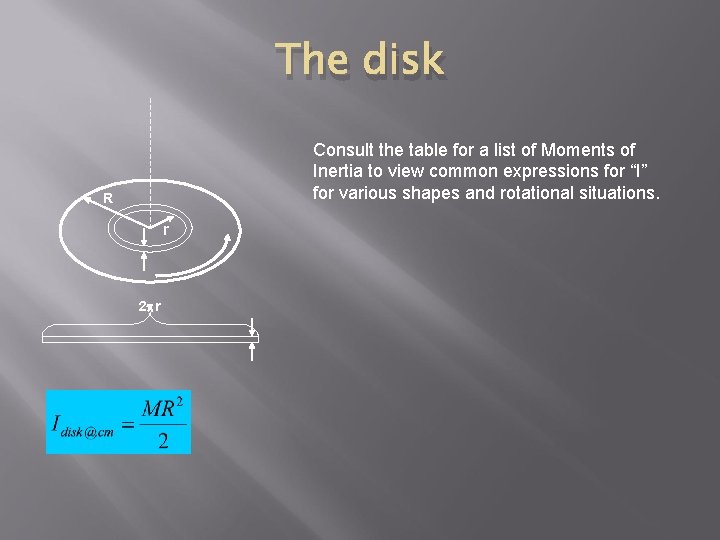
The disk Consult the table for a list of Moments of Inertia to view common expressions for “I” for various shapes and rotational situations. R r 2 pr

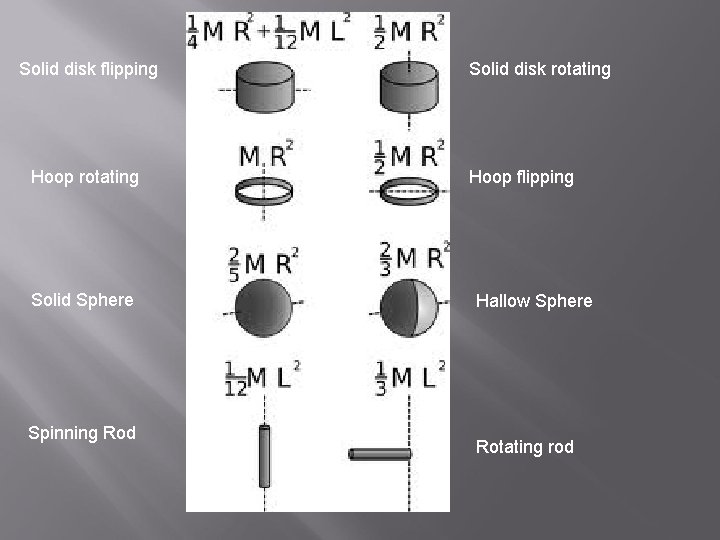
Solid disk flipping Hoop rotating Solid Sphere Spinning Rod Solid disk rotating Hoop flipping Hallow Sphere Rotating rod

Example Problem A playground merry-go-round of radius 2. 00 m has a moment of inertia I = 275 kg m 2 and is rotating about a frictionless vertical axle. As a child of mass 25. 0 kg stands at a distance of 1. 00 m from the axle, the system (merry-go-round and child) rotates at the rate of 14. 0 rev/min. The child then proceeds to walk toward the edge of the merry-go-round. What is the angular speed of the system when the child reaches the edge? Solution (details given in class): 1. 17 rad/s

Cross Product l The above formula for the cross product is useful when the magnitudes of the two vectors and the angle between them are known. l If you only know the components of the two vectors: Components of cross product vector

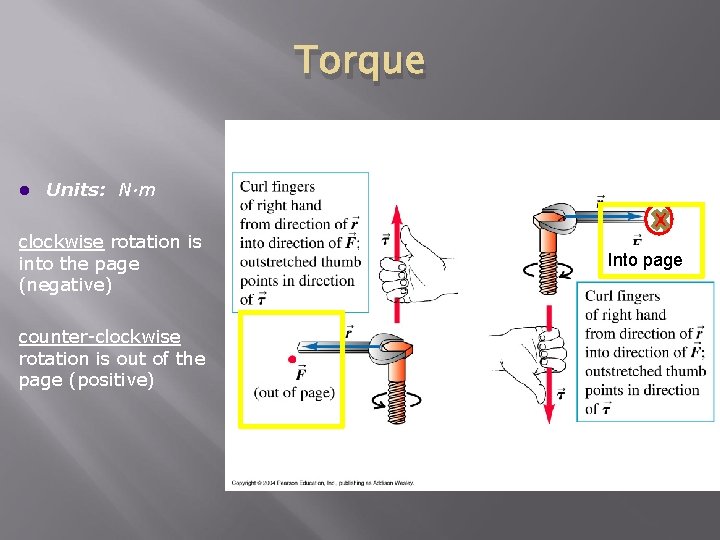
Torque l Units: N·m clockwise rotation is into the page (negative) counter-clockwise rotation is out of the page (positive) Into page

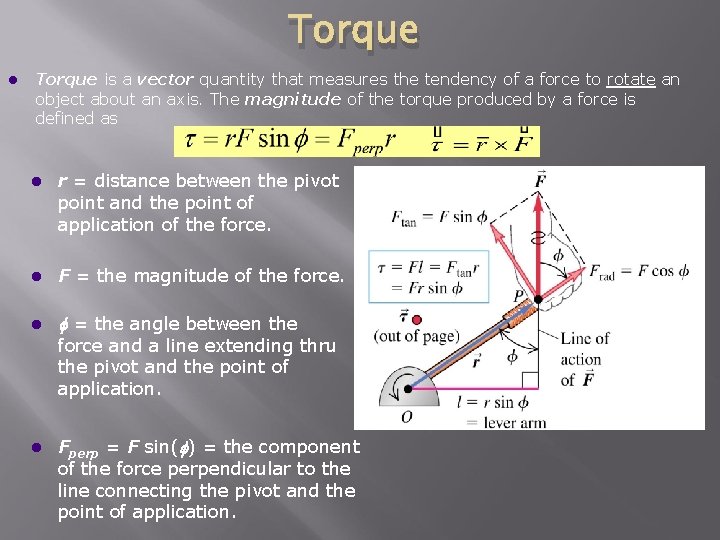
Torque l Torque is a vector quantity that measures the tendency of a force to rotate an object about an axis. The magnitude of the torque produced by a force is defined as l r = distance between the pivot point and the point of application of the force. l F = the magnitude of the force. l f = the angle between the force and a line extending thru the pivot and the point of application. l Fperp = F sin(f) = the component of the force perpendicular to the line connecting the pivot and the point of application.

Torque What is the best way to loosen a bolt using a wrench? Notice that where you exert the force matters! Which of the following forces is most likely to loosen the bolt (assuming they all have the same magnitude): Bolt l. B B l. C C A (l. A = 0) Answer: Force C, because the tendency of a force to cause a rotation about some point depends on its magnitude and the perpendicular distance l between the line of action of the force and that point Point about which bolt rotates Line of action of force A Line of action of force B Line of action of force C

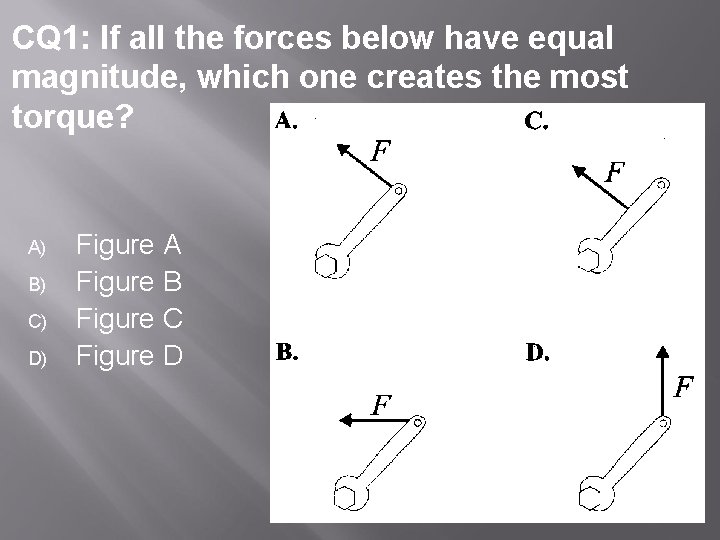
CQ 1: If all the forces below have equal magnitude, which one creates the most torque? A) B) C) D) Figure A Figure B Figure C Figure D

CQ 2: A carpenter who is having a difficult time loosening a screw puts away his screwdriver and chooses another with a handle with a larger diameter. He does this because: A) B) C) D) increasing force increases torque. decreasing force decreases torque. increasing lever arm increases torque. decreasing lever arm decreases torque.

Torque and Angular Acceleration for a Rigid Body N 2 L for a rigid body in rotational form In equilibrium the net torque is zero ONLY external torques affect the rigid body’s rotation!

N 2 L in Rotational Form Problem-Solving Strategy IDENTIFY the relevant concepts: z=I z SET UP the problem using the following steps: 1. Sketch 2. Free-body diagram 3. Coordinate axes for each body and indicate a positive sense of rotation for each rotating body. EXECUTE the solution as follows: Plug and chug EVALUATE your answer: Check that the algebraic signs of your results make sense.

Equilibrium of a Rigid Body We can apply Newton’s 1 st law two different ways to a rigid body when it is in equilibrium For translational equilibrium: Linear acceleration For rotational equilibrium: Angular acceleration

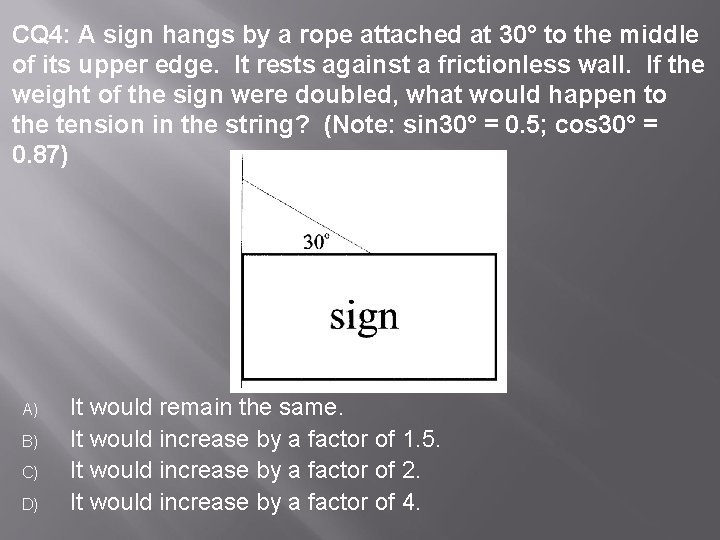
CQ 4: A sign hangs by a rope attached at 30° to the middle of its upper edge. It rests against a frictionless wall. If the weight of the sign were doubled, what would happen to the tension in the string? (Note: sin 30° = 0. 5; cos 30° = 0. 87) A) B) C) D) It would remain the same. It would increase by a factor of 1. 5. It would increase by a factor of 2. It would increase by a factor of 4.

CQ 5: A telephone pole stands as shown below. Line A is 4 m off the ground and line B is 3 m off the ground. The tensions in line A and line B are 200 N and 400 N respectively. What is the net torque on the pole? A) B) C) D) 0 Nm 400 Nm 800 Nm 2000 Nm

Example Problem An 8. 00 -m, 200 -N uniform ladder rests against a smooth wall. The coefficient of static friction between the ladder and the ground is 0. 600, and the ladder makes a 50. 0° angle with the ground. How far up the ladder can an 800 -N person climb before the ladder begins to slip? Solution (details in class): 6. 15 m

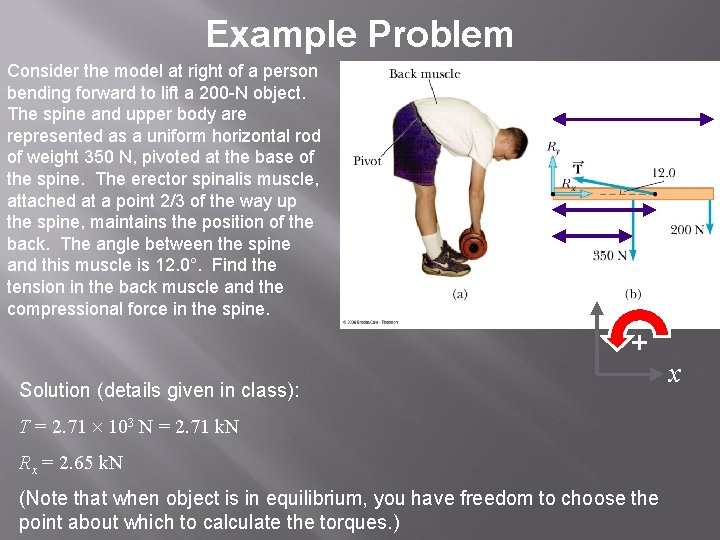
Example Problem Consider the model at right of a person bending forward to lift a 200 -N object. The spine and upper body are represented as a uniform horizontal rod of weight 350 N, pivoted at the base of the spine. The erector spinalis muscle, attached at a point 2/3 of the way up the spine, maintains the position of the back. The angle between the spine and this muscle is 12. 0°. Find the tension in the back muscle and the compressional force in the spine. l 2 l/3 l/2 y + Solution (details given in class): T = 2. 71 103 N = 2. 71 k. N Rx = 2. 65 k. N (Note that when object is in equilibrium, you have freedom to choose the point about which to calculate the torques. ) x

Example Problem An Atwood’s machine consists of blocks of masses m 1 = 10. 0 kg and m 2 = 20. 0 kg attached by a cord running over a pulley as shown. The pulley is a solid cylinder with mass M = 8. 00 kg and radius r = 0. 200 m. The block of mass T 1 T 2 m 2 is allowed to drop, and the cord turns the pulley without slipping. (a) Why must the tension T 2 be greater than the tension T 1? (b) What is the acceleration of the system, assuming the pulley axis is frictionless? (c) Find the tensions T 1 and T 2. Solution (details given in class): (b) 2. 88 m/s 2 (c) T 1 = 127 N, T 2 = 138 N

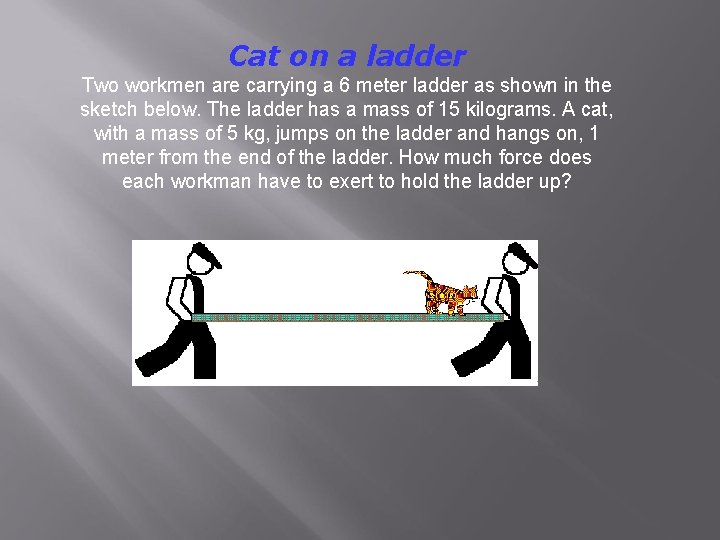
Cat on a ladder Two workmen are carrying a 6 meter ladder as shown in the sketch below. The ladder has a mass of 15 kilograms. A cat, with a mass of 5 kg, jumps on the ladder and hangs on, 1 meter from the end of the ladder. How much force does each workman have to exert to hold the ladder up?