Recap Lecture 14 Kleenes theorem part III method


















- Slides: 21

Recap Lecture 14 • Kleene’s theorem part III (method 2: Concatenation of FAs) continued, Kleene’s theorem part III (method 3: closure of an FA), Examples 1

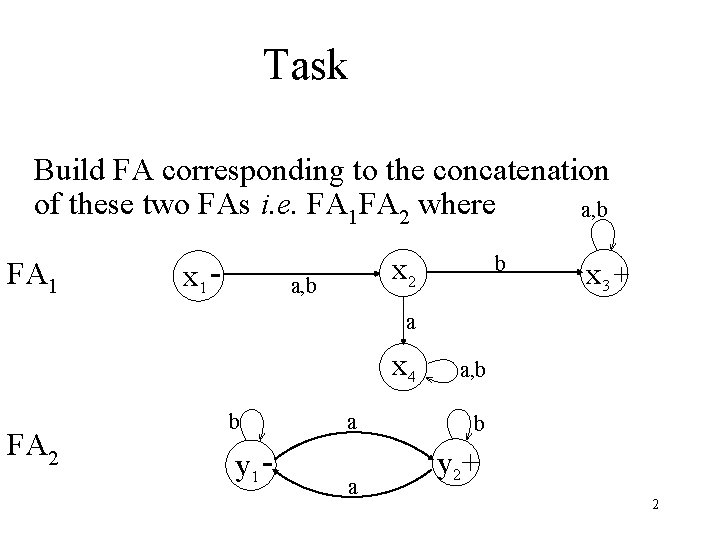
Task Build FA corresponding to the concatenation of these two FAs i. e. FA 1 FA 2 where a, b FA 1 x 1 - x 2 a, b b x 3 + a x 4 FA 2 b y 1 - a a a, b b y 2+ 2

Task solution • RE corresponding to FA 1 may be (a+b)b(a+b)* with b as second letter • RE corresponding to FA 2 may be (a+b)b(a+b)* b*a(b+ab*a)* with odd number of a’s 3

Solution continued … x 1 - x 2 a, b b a, b x 3 + a x 4 b y 1 Old States z 1 - x 1 a a a, b b y 2+ New States after reading a x 2 z 2 b x 2 z 2 4

Solution continued … Old States New States after reading a b z 2 x 4 z 3 (x 3, y 1) z 4 z 3 x 4 z 3 z 4 (x 3, y 1) (x 3 , y 1, y 2) z 5 (x 3, y 1) z 4 z 5+ (x 3, y 1 , y 2) (x 3 , y 1 , y 2) z 5 (x 3, y 1 , y 2) z 5 5

Solution continued … b a, b z 4 • -z 1 a, b z 2 a • +z 5 b a a, b z 3 6

Note • It is to be noted that as observed in the previous examples, if at the initial state of the given FA, there is either a loop or an incoming transition edge, the initial state corresponds to the final state and a non-final state as well, of the required FA, otherwise the initial state of given FA will only correspond to a single state of the required FA (i. e. the initial state which is final as well). 7

Task • Build an FA corresponding to the closure of the following FA b y 1± a a b y 2 8

Nondeterministic Finite Automaton (NFA) Definition: An NFA is a TG with a unique start state and a property of having single letter as label of transitions. An NFA is a collection of three things 1) Finite many states with one initial and some final states 2) Finite set of input letters, say, ={a, b, c} 3) Finite set of transitions, showing where to move if a letter is input at certain state ( is not a valid transition), there may be more than one transition for certain letters and there may 9 not be any transition for certain letters.

Observations It may be observed, from the definition of NFA, that the string is supposed to be accepted, if there exists at least one successful path, otherwise rejected. It is to be noted that an NFA can be considered to be an intermediate structure between FA and TG. The examples of NFAs can be found in the following 10

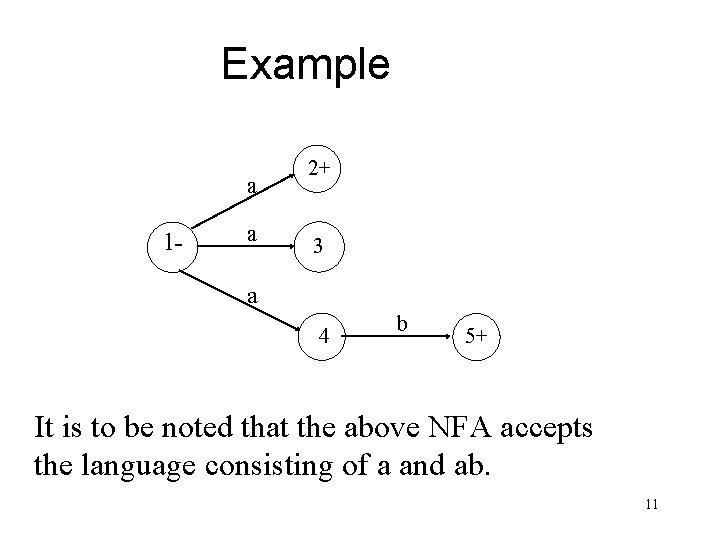
Example a 1 - a 2+ 3 a 4 b 5+ It is to be noted that the above NFA accepts the language consisting of a and ab. 11

Example a, b 1 - a, b a 2 a 3+ It is to be noted that the above NFA accepts the language of strings, defined over Σ = {a, b}, containing aa. 12

Note • It is to be noted that NFA helps to eliminate a loop at certain state of an FA. This process is done converting the loop into a circuit. But during this process the FA remains no longer FA and is converted to a corresponding NFA, which is shown in the following example. 13

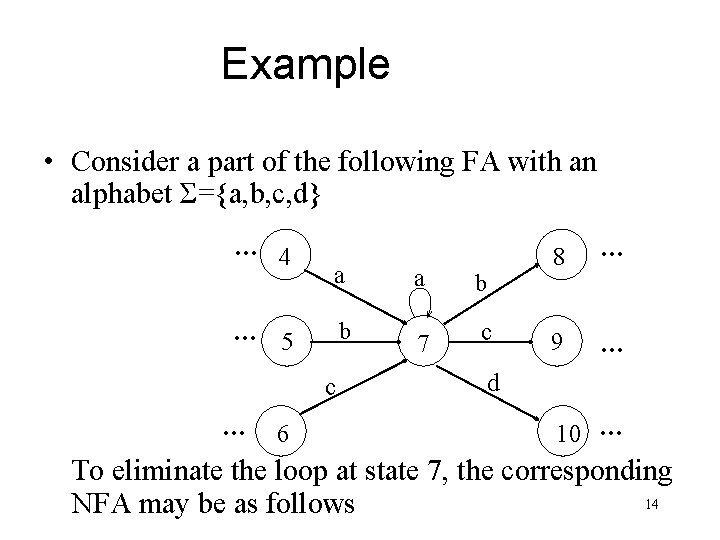
Example • Consider a part of the following FA with an alphabet Σ={a, b, c, d} … 4 a b … 5 c … 6 a 7 b c 8 … 9 … d 10 … To eliminate the loop at state 7, the corresponding 14 NFA may be as follows

Example continued. . . … 4 b 11 c a … 5 … 6 a a b c 7 8 … 9 … d b c d 10 … 15

Converting an FA to an equivalent NFA • It is to be noted that according to the Kleene’s theorem, if a language can be accepted by an FA, then there exists a TG accepting that language. Since, an NFA is a TG as well, therefore there exists an NFA accepting the language accepted by the given FA. In this case these FA and NFA are said to be equivalent to each others. Following are the examples of FAs to be converted to the equivalent NFAs 16

Example • Consider the following FA corresponding to (a+b)*b a b b - + a • The above FA may be equivalent to the following NFA a, b - b + Can the structure of above NFA be compared with the corresponding RE ? 17

Example • Consider the following FA b a, b a - b a 1 + • The above FA may be equivalent to the following NFA a, b - a 1 a, b a • Can the structure of above NFA be compared with the corresponding RE ? + 18

Task Build an NFA equivalent to the following FA a 2 4 a a b a 1– b 6+ a b 3 a, b b b 5 19

Application of an NFA • There is an important application of an NFA in artificial intelligence, which is discussed in the following example of a maze - 1 2 3 4 L 5 O 6 M 7 P 8 N 9 + 20

Summing Up • Examples of Kleene’s theorem part III (method 3), NFA, examples, avoiding loop using NFA, example, converting FA to NFA, examples, applying an NFA on an example of maze 21
 Kleene's theorem solved examples
Kleene's theorem solved examples Union of two fas
Union of two fas Stokes theorem is a relation between
Stokes theorem is a relation between Hamlet act iii scene ii
Hamlet act iii scene ii 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Va professional standards board
Va professional standards board Shawshank redemption summary
Shawshank redemption summary Summary of chapter 8 great gatsby
Summary of chapter 8 great gatsby Price matching
Price matching What is the purpose of an iteration recap
What is the purpose of an iteration recap Recap intensity clipping
Recap intensity clipping 60 minutes recap
60 minutes recap Recap database
Recap database Bracket power rule
Bracket power rule Introduction for recap
Introduction for recap Recap introduction
Recap introduction Recap from last week
Recap from last week The crucible discussion questions act 1
The crucible discussion questions act 1 Ezekiel cheever motivation
Ezekiel cheever motivation Logbook recap example
Logbook recap example Ytm recap
Ytm recap Black box recap
Black box recap







































