Rate of Change and Slope I can and

Rate of Change and Slope I can and I will find rates of change and slopes.

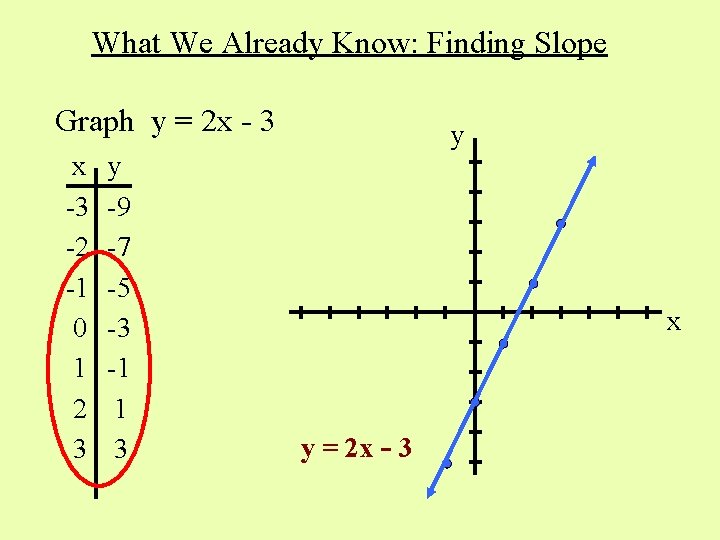
What We Already Know: Finding Slope Graph y = 2 x - 3 x -3 -2 -1 0 1 2 3 y -9 -7 -5 -3 -1 1 3 y x y = 2 x - 3

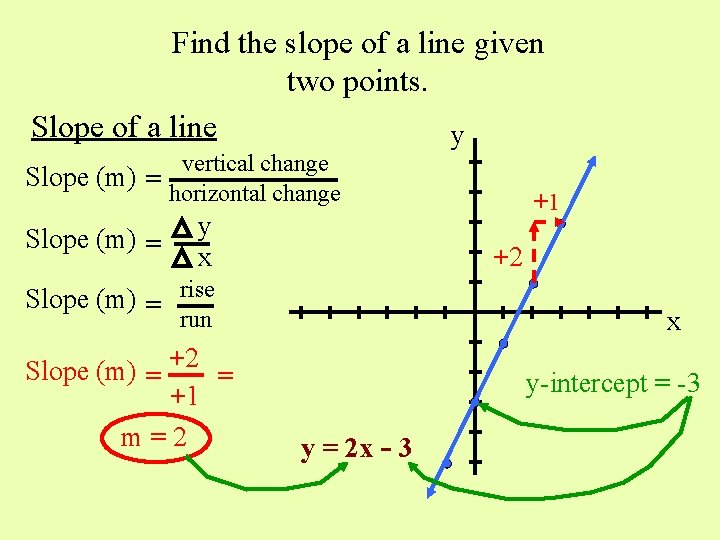
Find the slope of a line given two points. Slope of a line y vertical change Slope (m) = horizontal change Slope (m) = y x Slope (m) = rise run Slope (m) = +2 = +1 m=2 +1 +2 x y-intercept = -3 y = 2 x - 3

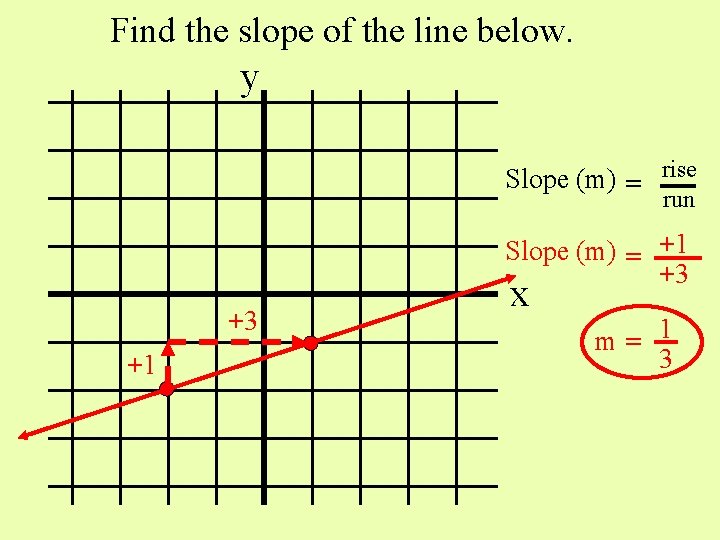
Find the slope of the line below. y Slope (m) = rise run Slope (m) = +1 +3 +3 +1 x m= 1 3

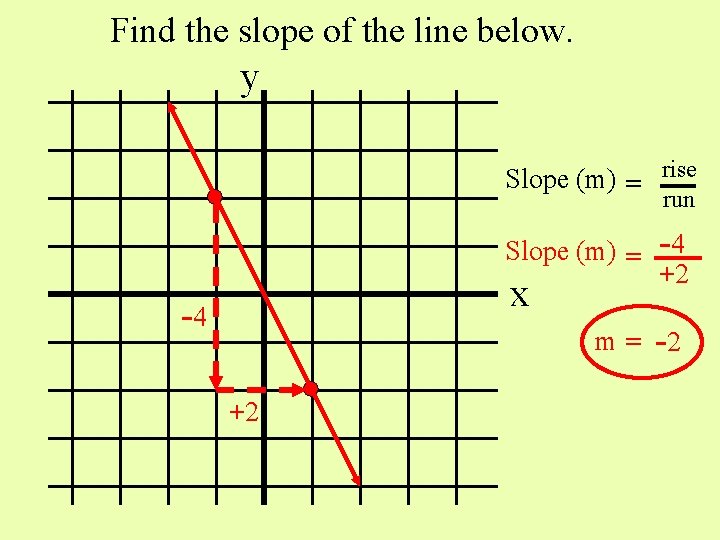
Find the slope of the line below. y Slope (m) = rise run Slope (m) = x -4 -4 +2 m = -2 +2

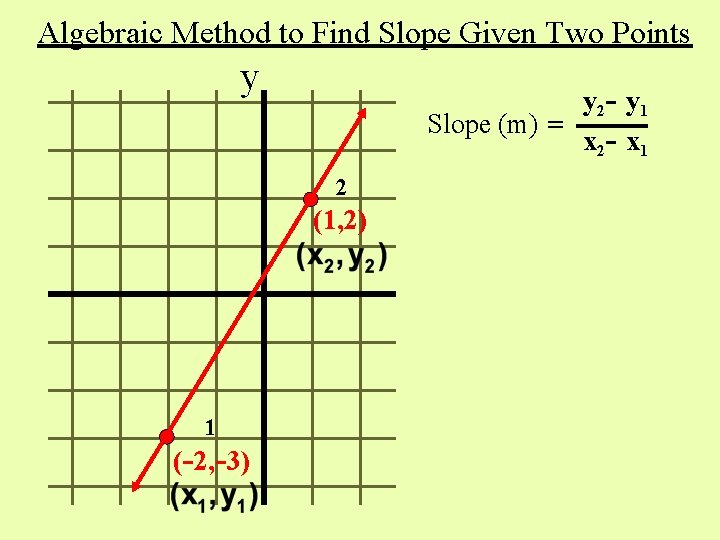
Algebraic Method to Find Slope Given Two Points y y 2 - y 1 Slope (m) = x 2 - x 1 2 (1, 2) 1 (-2, -3)

FORMULA for finding slope of a line if you know two points. y 2 - y 1 Slope (m) = x 2 - x 1

Ex. 1) Find the slope between (-1, 3) and (4, 7).

Ex. 2) Find the slope between (6, 5) and (-1, 7).

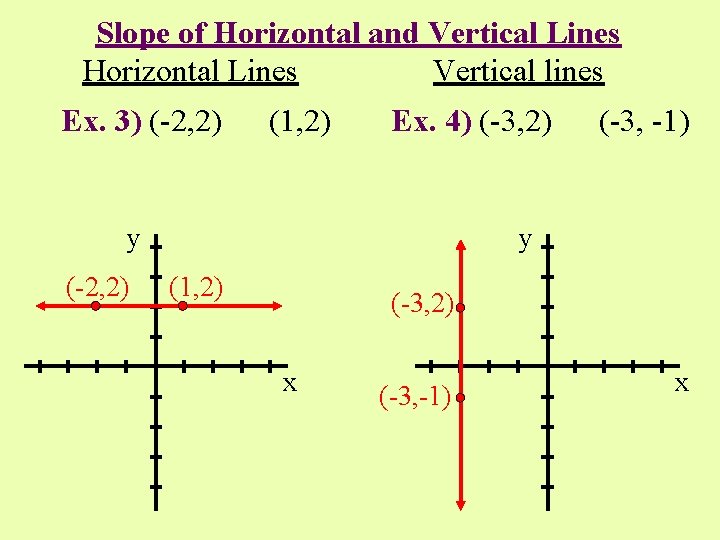
Slope of Horizontal and Vertical Lines Horizontal Lines Vertical lines Ex. 3) (-2, 2) (1, 2) Ex. 4) (-3, 2) y (-2, 2) (-3, -1) y (1, 2) (-3, 2) x (-3, -1) x

What is rate of change? • Rate: A ratio that compares two quantities. • Rate of Change: A ratio of the change in one quantity to a corresponding unit change in another quantity. • y 2 – y 1 x 2 – x 1

Ex. 5) The table shows the average temperature for five months in Dickson. Find the rate of change in the temperature between month 2 and month 7. Month 2 3 5 7 8 Temp 56 56 63 71 72

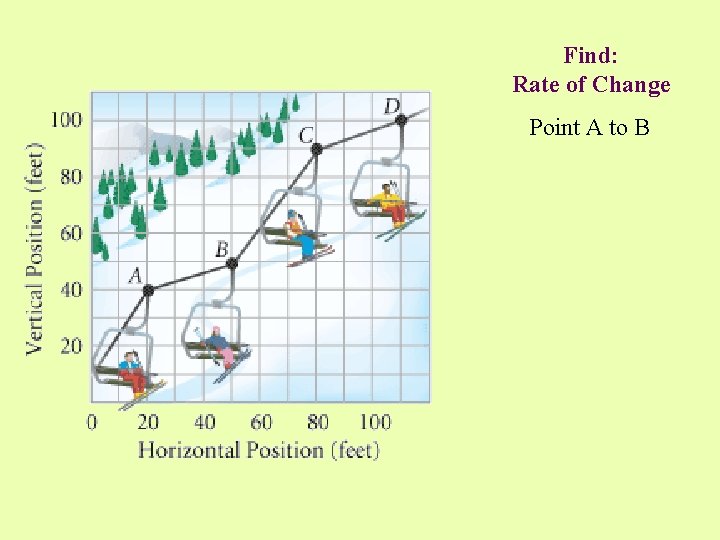
Find: Rate of Change Point A to B