2 2 Find Slope and Rate of Change

2. 2 Find Slope and Rate of Change Algebra II

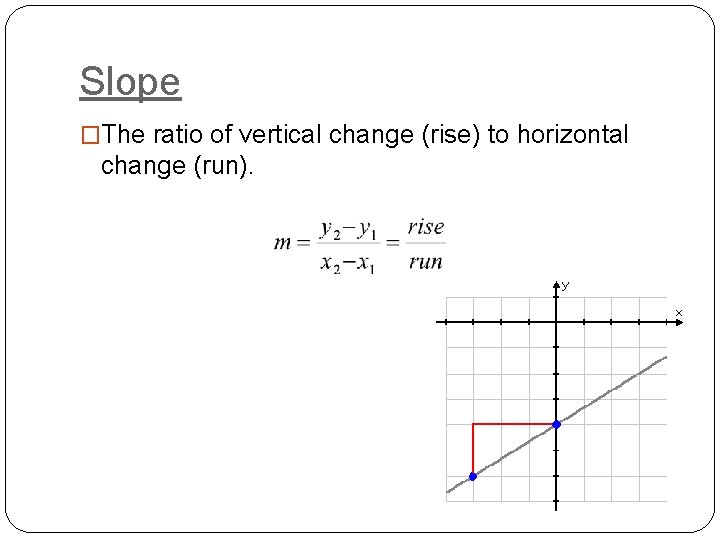
Slope �The ratio of vertical change (rise) to horizontal change (run).

Finding the slope of a line �Ex. 1 - Find the slope of the line passing through (-2, -4) and (3, -1).

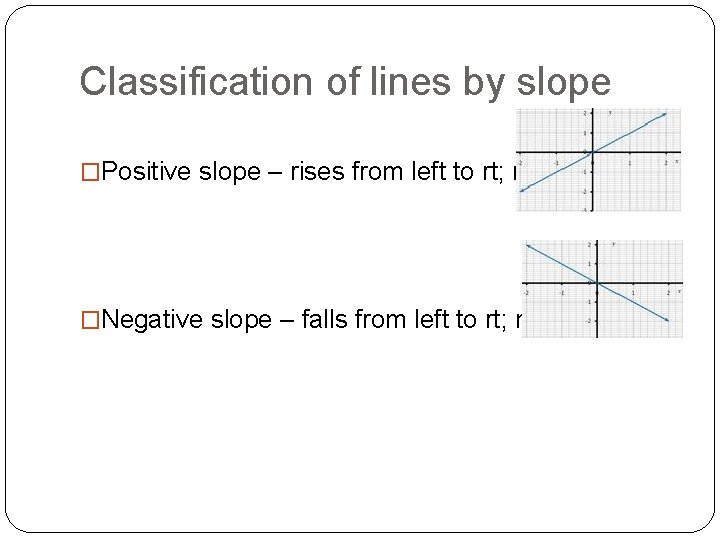
Classification of lines by slope �Positive slope – rises from left to rt; m>0 �Negative slope – falls from left to rt; m < 0

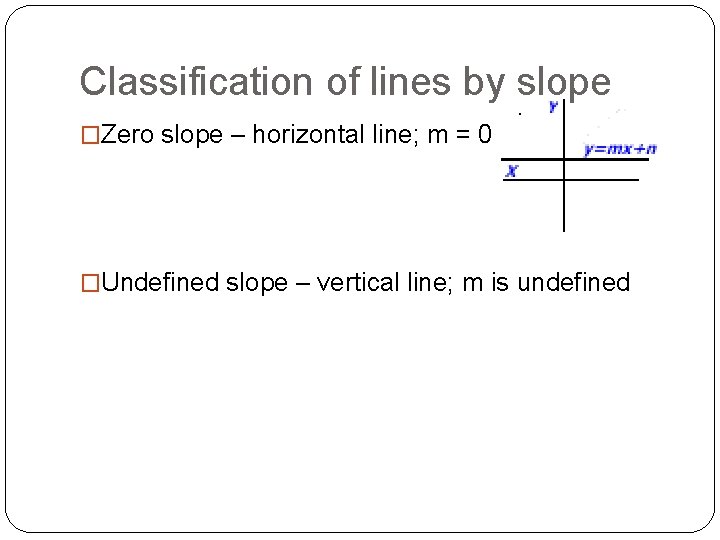
Classification of lines by slope �Zero slope – horizontal line; m = 0 �Undefined slope – vertical line; m is undefined

Classifying Lines using slope �Ex. 2 Without graphing, tell whether the line through the given points rises, falls, is horizontal or is vertical. �a. ) (-2, 3), (1, 5) �b. ) (1, -2), (3, -2)

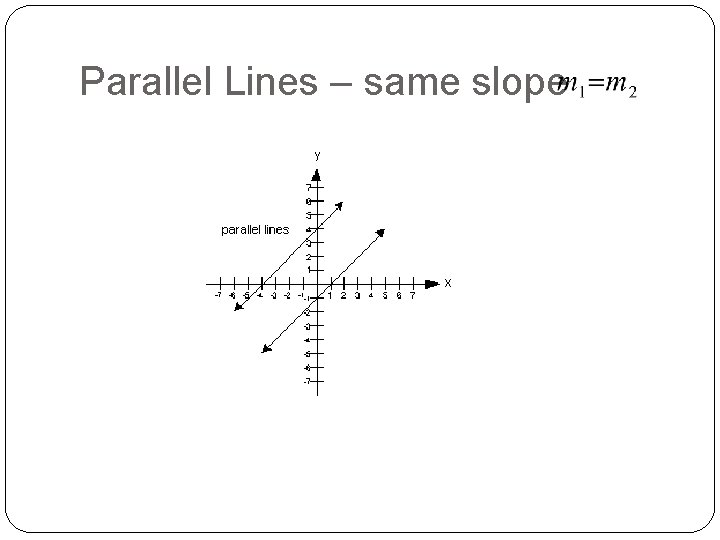
Parallel Lines – same slope

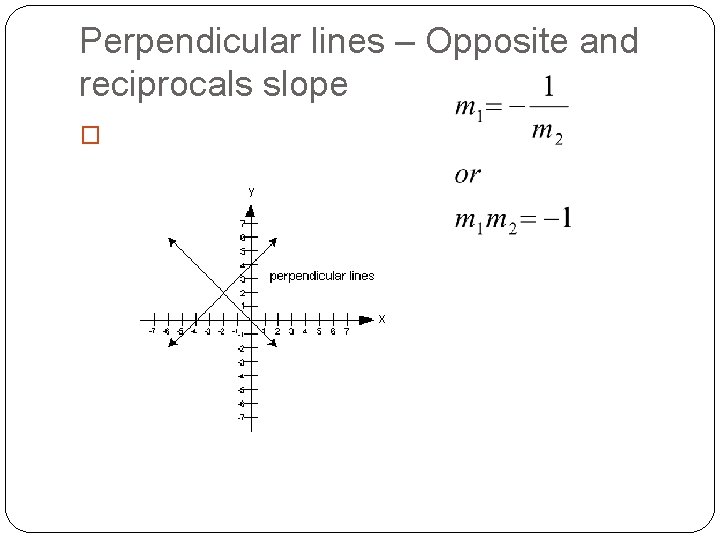
Perpendicular lines – Opposite and reciprocals slope �

Classifying Parallel & Perpendicular Lines �Ex. 4 Tell whether the lines are parallel, perpendicular, or neither. �Line 1: through (1, -2) and (3, -2) �Line 2: through ( -5, 4) and (0, 4)

Geometrical use of slope �Ex. 5 An escalator in an airport rises 28 ft over a horizontal distance of 48 feet. What is the slope of the escalator?

Slope as a rate of change �Ex. 6 Over a 30 day period, the amount of propane in a tank that stores propane for heating a home decreases from 400 gallons to 214 gallons. What is the average rate of change in the amount of propane?

Assignment �

Comparing Steepness �For two lines with positive slopes, the line with the greater slope is steeper. �For two lines with negative slopes, the line with the slope of greater absolute value is steeper. �Reminder: horizontal lines are “flat” and vertical lines are “infinitely steep”

Comparing Steepness of Lines �Ex. 3 Tell which line is steeper. �Line 1: through (1, -4) and (5, 2) �Line 2: through (-2, -5) and (1, -2)