1 4 Slope and Rate of Change Slope

§ 1. 4 Slope and Rate of Change

Slope of a Line Martin-Gay, Beginning and Intermediate Algebra, 4 ed 2

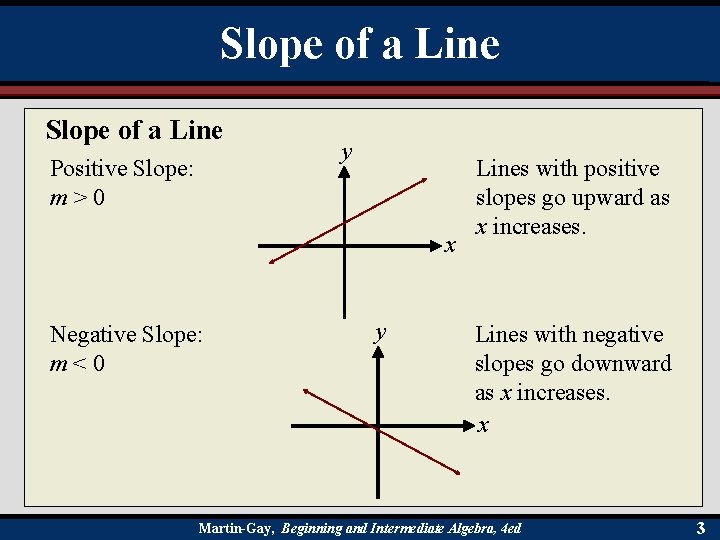
Slope of a Line Positive Slope: m>0 y x Negative Slope: m<0 y Lines with positive slopes go upward as x increases. Lines with negative slopes go downward as x increases. x Martin-Gay, Beginning and Intermediate Algebra, 4 ed 3

Finding the Slope Given Two Points Example: Find the slope of the line through (4, – 3 ) and (2, 2). If we let (x 1, y 1) = (4, – 3) and (x 2, y 2) = (2, 2), then Note: If we let (x 1, y 1) be (2, 2) and (x 2, y 2) be (4, – 3), then we get the same result. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 4

Slope-Intercept Form of a Line Slope-Intercept Form When a linear equation in two variables is written in the slope-intercept form, y = mx + b m is the slope and (0, b) is the y-intercept of the line. y = 3 x – 4 y The slope The -intercept is is 3. (0, -4). Martin-Gay, Beginning and Intermediate Algebra, 4 ed 5

Slope-Intercept Form of a Line Example: Find the equation of the line with slope (0, 5). slope: and y-intercept: Martin-Gay, Beginning and Intermediate Algebra, 4 ed 6

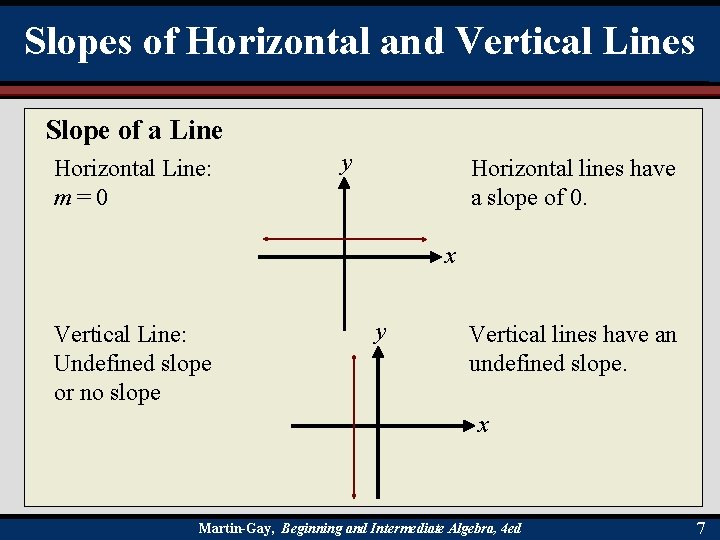
Slopes of Horizontal and Vertical Lines Slope of a Line Horizontal Line: m=0 y Horizontal lines have a slope of 0. x Vertical Line: Undefined slope or no slope y Vertical lines have an undefined slope. x Martin-Gay, Beginning and Intermediate Algebra, 4 ed 7

Slope of a Horizontal Line Any two points of a horizontal line will have the same y-values. This means that the y-values will always have a difference of 0 for all horizontal lines. All horizontal lines have a slope 0. y y=3 (0, 3) Martin-Gay, Beginning and Intermediate Algebra, 4 ed x 8

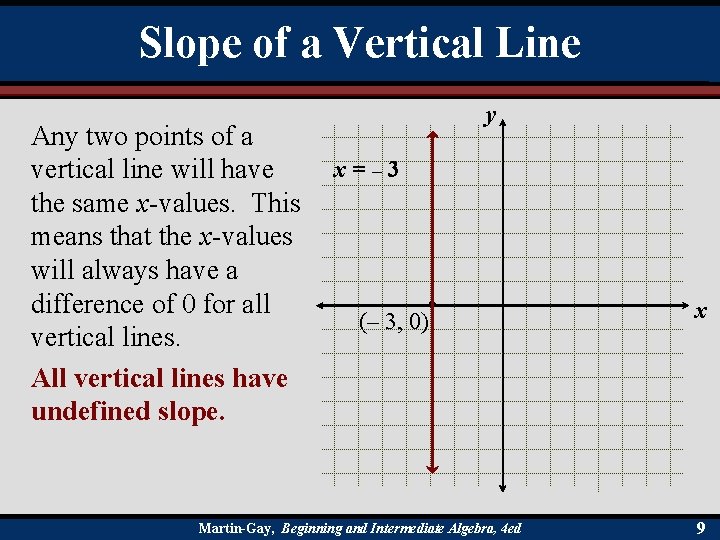
Slope of a Vertical Line Any two points of a vertical line will have the same x-values. This means that the x-values will always have a difference of 0 for all vertical lines. All vertical lines have undefined slope. y x=– 3 (– 3, 0) Martin-Gay, Beginning and Intermediate Algebra, 4 ed x 9

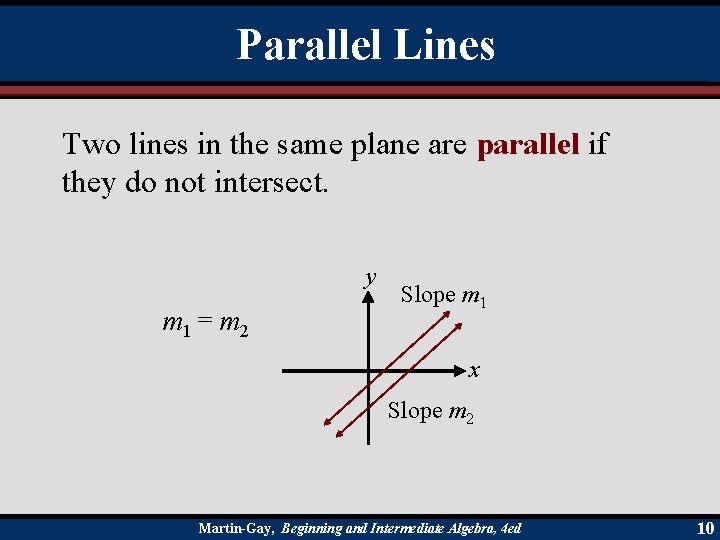
Parallel Lines Two lines in the same plane are parallel if they do not intersect. y m 1 = m 2 Slope m 1 x Slope m 2 Martin-Gay, Beginning and Intermediate Algebra, 4 ed 10

Parallel Lines Example: Determine whether the line 6 x + 2 y = 9 is parallel to – 3 x – y = 3. Find the slope of each line. 6 x + 2 y = 9 – 3 x – y = 3 The slopes are the same so the lines are parallel. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 11

Perpendicular Lines Two lines are perpendicular if they lie in the same plane and meet at a 90◦ (right) angle. The product of the slopes of two perpendicular lines is – 1. y m 1 m 2 = 1 or m 1 = Slope m 2 x Slope m 1 Martin-Gay, Beginning and Intermediate Algebra, 4 ed 12

Perpendicular Lines Example: Determine whether the line x + 3 y = – 15 is perpendicular to – 3 x + y = – 1. Find the slope of each line. x + 3 y = – 15 – 3 x + y = – 1 The slopes are negative reciprocals so the lines are perpendicular. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 13

Average Rate of Change Example: Becky decided to take a bike ride up a mountain trail. The trail has a vertical rise of 90 feet for every 250 feet of horizontal change. In percent, what is the grade of the trail? The grade of the trail is given by The grade of the trail is The slope of a line can also be interpreted as the average rate of change. It tells us how fast y is changing with respect to x. Martin-Gay, Beginning and Intermediate Algebra, 4 ed 14