4 3 Slope Slope of a Line Slope

4. 3 Slope

Slope of a Line Slope • steepness of a line • compares the vertical change to the horizontal change • also used for rate of change, grade, pitch Formula: The slope of the line through the points (x 1, y 1) and (x 2, y 2) is where x 1≠x 2

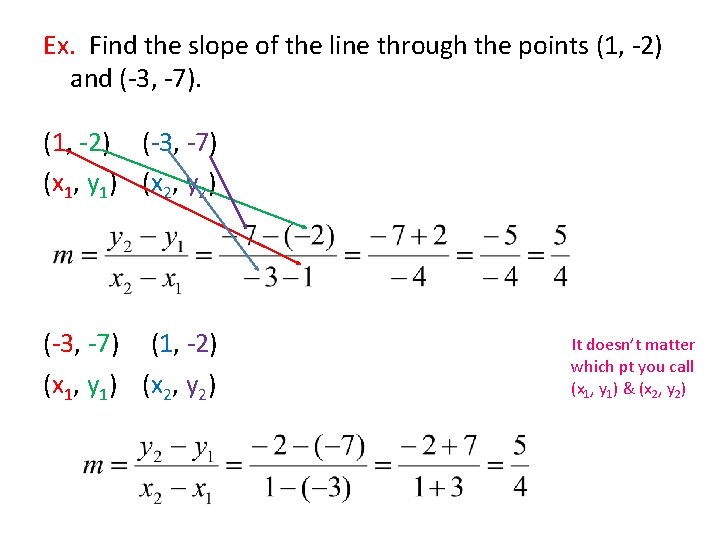
Ex. Find the slope of the line through the points (1, -2) and (-3, -7). (1, -2) (-3, -7) (x 1, y 1) (x 2, y 2) (-3, -7) (1, -2) (x 1, y 1) (x 2, y 2) It doesn’t matter which pt you call (x 1, y 1) & (x 2, y 2)

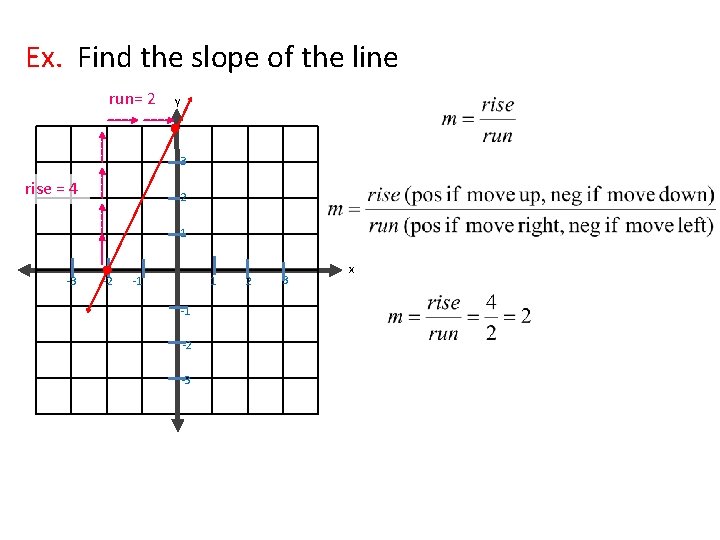
Ex. Find the slope of the line run= 2 y 3 rise = 4 2 1 -3 -2 -1 1 -1 -2 -3 2 3 x

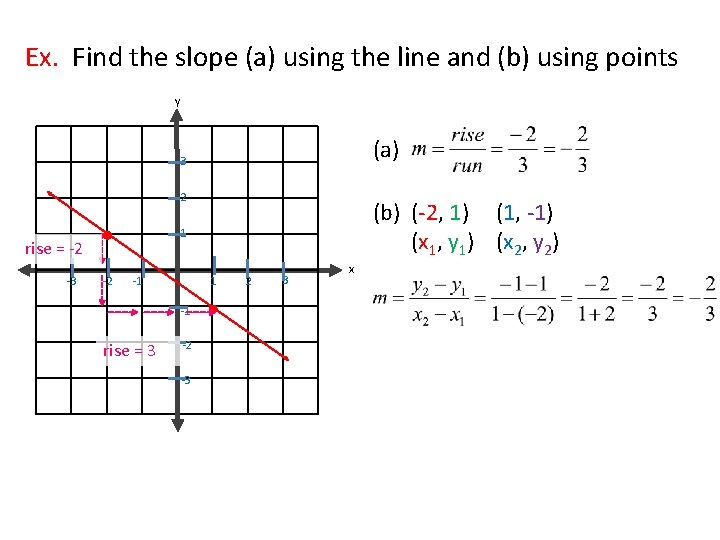
Ex. Find the slope (a) using the line and (b) using points y (a) 3 2 1 rise = -2 -3 (b) (-2, 1) (1, -1) (x 1, y 1) (x 2, y 2) -2 -1 1 -1 rise = 3 -2 -3 2 3 x

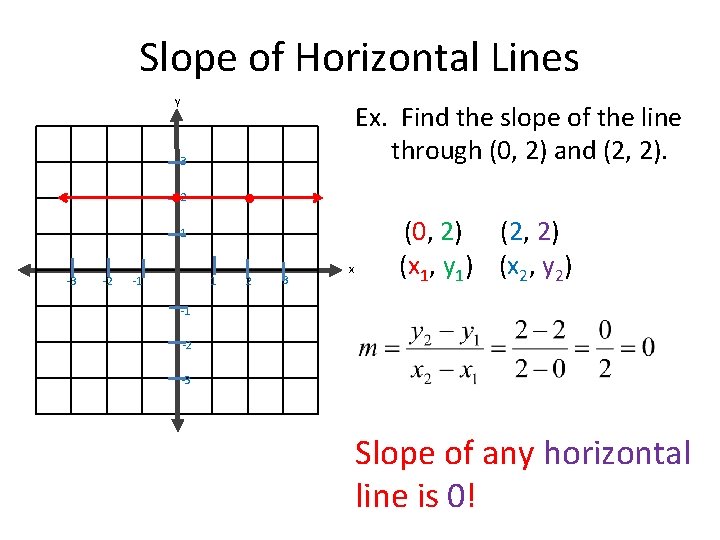
Slope of Horizontal Lines y Ex. Find the slope of the line through (0, 2) and (2, 2). 3 2 1 -3 -2 -1 1 2 3 x (0, 2) (2, 2) (x 1, y 1) (x 2, y 2) -1 -2 -3 Slope of any horizontal line is 0!

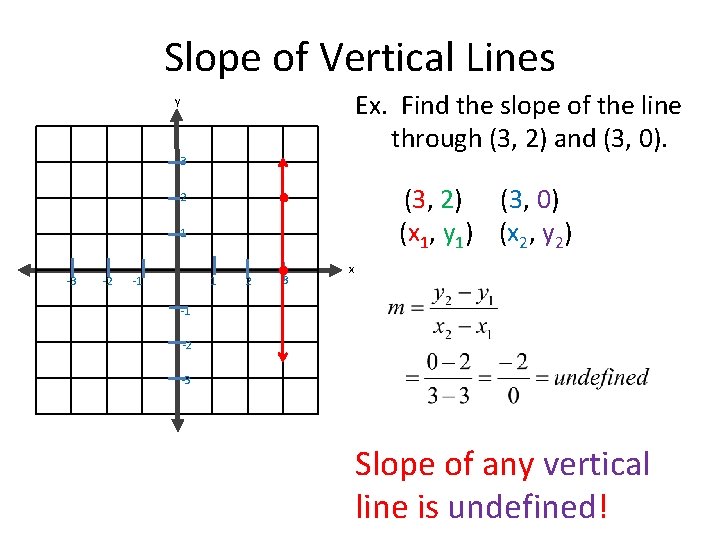
Slope of Vertical Lines Ex. Find the slope of the line through (3, 2) and (3, 0). y 3 (3, 2) (3, 0) (x 1, y 1) (x 2, y 2) 2 1 -3 -2 -1 1 2 3 x -1 -2 -3 Slope of any vertical line is undefined!

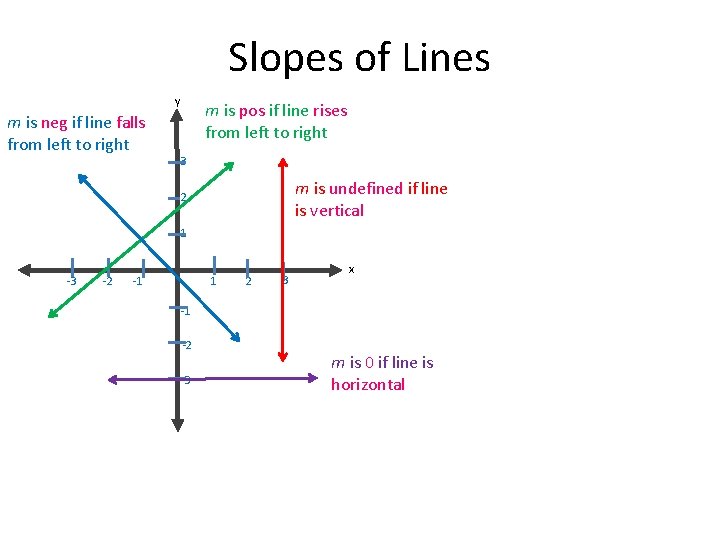
Slopes of Lines y m is neg if line falls from left to right m is pos if line rises from left to right 3 m is undefined if line is vertical 2 1 -3 -2 -1 1 2 3 x -1 -2 -3 m is 0 if line is horizontal

Parallel and Perpendicular Lines Parallel Lines Perpendicular Lines slopes are the same slopes are negative reciprocals (mult. to -1) (or hor. & vert)

Ex. Determine whether the lines through the points are parallel, perpendicular, or neither. (-2, -15) and (0, -3); (-12, 6) and (6, 3) Slope of the first line is 6 and the slope of the second line is -1/6, so slopes are negative reciprocals; therefore, the lines are perpendicular

Groups Page 254: 37, 39, 41