Propositional Logic Dr Rogelio Dvila Prez ProfesorInvestigador Divisin

Propositional Logic Dr. Rogelio Dávila Pérez Profesor-Investigador División de Posgrado Universidad Autónoma Guadalajara rdav 90@gmail. com

Propositional Logic History Logic is the study of reasoning. Logic became mathematical after the contributions of the British mathematician an philosopher George Bool (1815 -1864). His book “The Laws of Though”, introduces the meaning of the connectors AND, OR, CONDITIONAL, NOT. The German philosopher Gottlob Frege (1848 -1925) in his book “Ideography, a Formula language, Modeled upon that of Arithmetic, for Pure Thought” (1879), introduced the Quantification Logic. Alfred Tarsky (1902 -1983), mathematician and logician, remarked the importance of distinguishing between the object language and the metalanguage. - - The object language is the object of study and the metalanguage is the one we use to talk about the object one.

Propositional Logic I. Syntax 1. Vocabulary: The language of propositional logic has an alphabet consisting in: (a) Propositional variables: Pi, Qi, Ri (i N) (b) Logical constants: 1. Logical connectors: , , , (a) Auxiliary symbols: “(“, “)”, “, ” Well-formed formulas (wffs) 2. 1. (a) (b) 1. If is a propositional variable, then is a wff. is called contradiction an is a wff. If and are wffs, then , , , are also wffs. Nothing else is a wff.

Propositional Logic II. Rules of Inference (Natural Deduction [Gentsen, 60 s]) (a) Conjunction Rules -Intro -Elim n Conditional Rules -Intro … -Elim (modus ponens rule)

Propositional Logic (c) n Contradiction Rules -Intro Negation Rules -Intro … -Elim (Double negation rule)

Propositional Logic (e) Disjunction Rules -Intro -Elim

Propositional Logic An axiomatic system for propositional logic 1. Axiom schemata (A 1) (X (Y X)) (A 2) ((X (Y Z)) ((X Y) (X Z))) (A 3) (( X Y) X)) 2. Inference rules (MP) If X and (X Y) are both theorems then Y is a theorem. n We can use the equivalences ( )

Propositional Logic A traditional way of characterizing validity and logical consequence is in terms of derivation, or proof, and inference rules. This may be accomplished either by an axiomatic system or, through a natural deduction system. Some definitions: Def. An axiom is a statement considered as valid. Def. An inference rule is a machinery for producing new valid statements from previously obtained ones. Def. An axiomatic system consists of a set of axioms (or axioms schemata) and a set of inference rules. Def. In an axiomatic system, valid statements produced by the system are called theorems.

Propositional Logic Def. A derivation or proof of a theorem is the ordered list of axioms, theorems and statements produced by the application of inference rules on previously obtained theorems. Def. For an axiomatic system, derivability or provability, of a formula is written: ( is a theorem) Def. If is a set of formulas, the expression means that is derivable from . In this case the formulas in are considered as hypotheses. Def. Two formulas and are logically equivalent ( ), if each of them is provable from the other.

Propositional Logic Disjunctive Syllogism pvq ~p q Resolution rule [Robinson, 1965] p v q 1 v q 2 v … v q n ~p v r 1 v r 2 v … v rm q 1 v … v q n v r 1 v … v r m

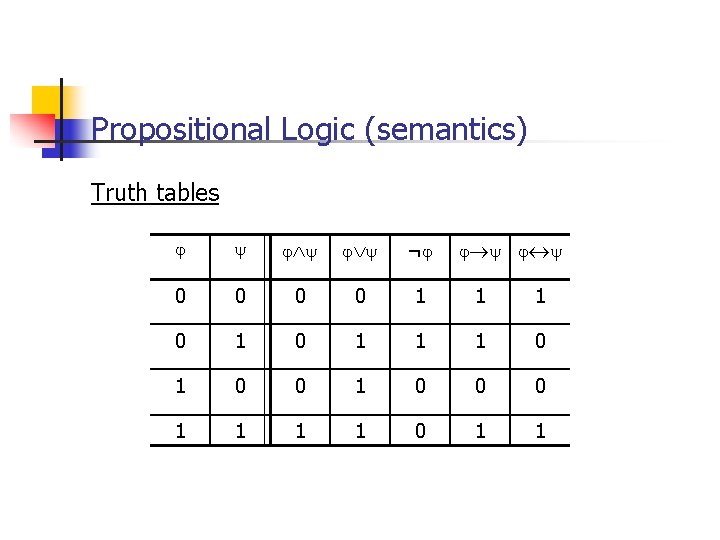
Propositional Logic (semantics) The purpose of semantics is to assign meaning to all the wellformed formulas in the language. n Definition. An interpretation of a formula of PL consists in assigning a truth value (0 -false, 1 -true), to each propositional symbol in the formula. The logical connectors are said to be truth-functional as their meaning is a function of the meanings of its constituents. It is common to express the meaning of logical connectors through a truth-table.

Propositional Logic (semantics) Truth tables ¬ 0 0 1 1 1 0 1 0 0 0 1 1

Propositional Logic (semantics) n n Definition. An interpretation that makes a formula true (=1) is a model of that formula. Definition. A formula is consistent, sound or satisfiable, if it has a model, otherwise it is inconsistent or unsatisfiable. Definition. A formula is valid when every interpretation of it is a model. This formula is called a tautology. Definition. A formula is contingent when it is not valid, but consistent. Some relations between the concepts: n n If is valid then ¬ is inconsistent If is consistent then ¬ is not valid.

Propositional Logic (semantics) Definition. Two wffs and are equivalent, , if both of them yield the same true values for any interpretation. Propositional logical equivalences (also called logical identities): (a) v (b) Contraposition Law: (c) Distributive Laws: (i) v ( ) ( v ) (ii) ( v ) ( ) v ( ) (e) De. Morgan’s Laws: (i) ( v ) (ii) ( ) v

Propositional Logic (semantics) Definition. An interpretation function or interpretation is a function that assigns a truth value to each propositional variable in the formula. Definition. A mapping v: PROP {0, 1} is a interpretation if: v( ) = min(v( ), v( )) v( ) = max(v( ), v( )) v( ) = 0 iff v( )=1 and v( )=0 v( ) = 1 iff v( )=v( ) = 1 - v( )

Propositional Logic Definition. (i) is a tautology if v( ) = 1 for all interpretations v, (ii) stands for ‘ p is a tautology’ Definition. A set of wffs is consistent, sound, or satisfiable, if all their elements admit the same model. Otherwise it is said to be inconsistent. Definition. Let be a set of wffs and a wff, we say that entails , or that is a logical consequence of , , iff every model of is a model of . Definition. is a logical consequence of , iff is a tautology.

Propositional Logic Theorem. For any set of formulas and any formulas and , if { } then . This fact is known as the deductive theorem. The deductive theorem for first order logic was first proved by the French mathematician Jacques Hebrand (1908 -1931). The converse of the deduction theorem is also true.

Propositional Logic Soundness and Completeness There are two important definitions that connect inference with entailment: 1. If, for any set of wffs, , and wff , implies that , we say that the set of inference rules, , is sound. If, for any set of wffs, , and wff , it is the case that whenever , there exists a proof of from , , using the set of inference rules, , we say that is complete. The completeness of a formal system of propositional logic was first proved by Emil Post in 1921.

Propositional Logic PSAT Problem The problem of finding at least one model of the set of formulas that is also a model of the formula , is known as the propositional satisfiability (PSAT) problem. An exhaustive procedure for solving the PSAT problem is to try systematically all of the ways to assign True and False to the atoms in the formula, checking the assignment to see if all formulas have value True under that assignment. If there are n atoms in the formula, there are 2 n different assignments, so for large n, the exhaustive procedure is computationally infeasible, thus the general PSAT problem is NP-complete.