Property Matching and Weighted Matching Amihood Amir Eran































- Slides: 32

Property Matching and Weighted Matching Amihood Amir, Eran Chencinski, Costas Iliopoulos, Tsvi Kopelowitz and Hui Zhang

Results Weighted Matching General Reduction Property Matching Property Indexing Pattern Matching

Property Matching Def: A property of a string T = t 1, …, tn is a set of intervals {(s 1, f 1), (s 2, f 2), … , (st, ft)}, s. t. si, fi {1, … , n} and si ≤ fi Property Matching Problem Given a text T with property and a pattern P, Find all locations where P matches T and is fully contained in an interval in.

Property Matching - Example Property Swap Matching Problem A A A D B B A B D D B A D B D A D B

Property Matching Solving Property Matching Problem • Solve regular pattern matching problem • Eliminate results not in property interval • Eliminating results can be done in linear time • If regular problem takes Ω(n) time => Property matching time = regular problem time

Property Indexing Problem • Preprocess T s. t. given a P find occurrences of P in T s. t. P is contained in a property interval • Time: proportional to |P| and tocc • Our solution: Query time O(|P| log|Σ| + tocc ) Preprocessing of O(n log|Σ| + n * log n)

Weighted Sequence Def 1: weighted sequence is sequence of sets of pairs where and is probability of having symbol at location i. <A, 1/2><A, 1/3> <A, 1/4> <B, 1/2><B, 1/9> <B, 3/8><B, 1/3> <D, 1> <C, 3/4> <C, 1/2><C, 8/9> <C, 1/8><D, 1/3>

Weighted Sequence Def 2: Given prob ε, P=p 1, …, pm occurs at location i of weighted text T w. p. at least ε if:

Weighted Sequence <A, 1/2><A, 1/3> <A, 1/4> <B, 1/2><B, 1/9> <B, 3/8><B, 1/3> <D, 1> <C, 3/4> <C, 1/2><C, 8/9> <C, 1/8><D, 1/3> A D C C

Goal • Weighted Matching problems = Pattern Matching problems with weighted text. • Goal: Find general reduction for solving weighted matching problems using regular pattern matching algorithms.

Naive Algorithm A 1. Find all possible patterns appearing in weighted text. 2. Concatenate all patterns to create new text. 3. Run regular pattern matching algorithm on new regular text. 4. Check each pattern found for prob. ≥ ε.

Naive Algorithm <A, 1/2><A, 1/3> <A, 1/4> <B, 1/2><B, 1/9> <B, 3/8><B, 1/3> <D, 1> <C, 3/4> <C, 1/2><C, 8/9> <C, 1/8><D, 1/3> D B B A A A D B C A A A D C B A A A D C C D B B A A C D B C A A C D C B A A C D C C D B B A

Naive Algorithm • Clearly this algorithm is inefficient and can be • exponential even for |Σ|=2. Notice that there is a lot of waste: – Many patterns share same substrings. – Given ε, we can ignore patterns w. p. < ε.

Maximal Factor Def 3: Given ε, weighted text T, string X is maximal factor of T at location i if: (a) X appears at location i w. p. ≥ ε (b) if we extend X with 1 character to right or left – the probability drops below ε.

Maximal Factor <A, 1/2><A, 1/3> <A, 1/4> <B, 1/2><B, 1/9> <B, 3/8><B, 1/3> <D, 1> <C, 3/4> <C, 1/2><C, 8/9> <C, 1/8><D, 1/3> A C D B

Algorithm B 1. Find all maximal factors in text. 2. Concatenate factors to create new text. 3. Run regular pattern matching algorithm on new regular text. Note: A pattern appearing in new text has prob. of appearance ≥ ε.

Total Length of Maximal Factors What is total length of all maximal factors? Consider the following case: <A, 1 -δ> <B, δ> <A, 1 -δ> <C, 1> <B, δ> <A, 1 -δ> <B, δ> such that (1 -δ)n/3 = ε. Þ n/3 maximal factors of length 2/3*n Þ Total length of all maximal factors is Ω(n 2).

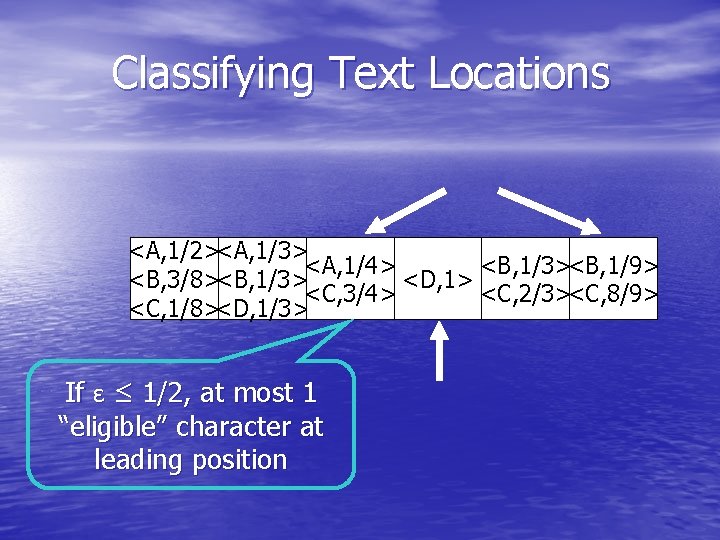
Classifying Text Locations Given ε, we classify location i of weighted text into 3 categories: • Solid positions: one character w. p. exactly 1. • Leading positions: at least one character w. p. greater than 1 -ε (and less than 1). • Branching positions: all characters have probability of appearance at most 1 -ε.

Classifying Text Locations <A, 1/2><A, 1/3> <A, 1/4> <B, 1/3><B, 1/9> <B, 3/8><B, 1/3> <D, 1> <C, 3/4> <C, 2/3><C, 8/9> <C, 1/8><D, 1/3> If ε ≤ 1/2, at most 1 “eligible” character at leading position

LST Transformation Def 4: The Leading to Solid Transformation of weighted text T=t 1, …, tn, LST(T)=t’ 1, …, t’n is: where leading character has prob. of app. ≥ max{1 -ε, ε}

LST Transformation <A, 1/2><A, 1/3> <A, 1/4> <B, 1/3><B, 1/9> <B, 3/8><B, 1/3> <C, 1> <D, 1> <C, 3/4> <C, 2/3><C, 8/9> <C, 1/8><D, 1/3>

Extended Maximal Factor Def 5: X is an extended maximal factor of T if X is an maximal factor of LST(T). <A, 1 -δ> <A, 1> <B, δ> <A, 1 -δ> <A, 1> <C, 1> <B, δ> <A, 1 -δ> <C, 1> <A, 1> <B, δ> <A, 1 -δ> <A, 1> <B, δ>

Lemma 1: Total length of all extended maximal factors is at most O(n∙(1/ε)2 log(1/ε)). Corollary: For constant k, total length of all extended maximal factors is linear.

Lemma 1 Why can we assume constant ε? • In practice: want patterns that appear with noticeable probabilities e. g. 90%, 50% or 20%. • Finding patterns w. p. at least 20% => 1/ε=5. • Smaller percentage = smaller ε, rarely in practice.

Proof of Lemma 1 Case 1: ε > 1/2, search patterns w. p. > 50%. Obv: At each location at most 1 char w. p. > 50%. Þ Total length of all factors is ≤ n. For rest of proof we assume ε ≤ 1/2.

Proof of Lemma 1 Claim 1: A (extended) maximal factor passes by at most O((1/ε)∙log(1/ε)) branching positions. Proof: Denote lb = max. # of branching position passed. In a branching position all characters have prob. of appearance ≤ 1 -ε :

Proof of Lemma 1 Claim 2: At most extended maximal factors start at each location. Intuition: <A 1, ε> <A 2, ε> <B, 1> <C, 1> <A 1/ε, ε> <B 1, 2ε> <A 1, 1/2> <B 2, 2ε> <C, 1> <A 2, 1/2> <B 1/2ε, 2ε>

Proof of Lemma 1 Claim 1: A (extended) maximal factor passes by ≤ O((1/ε) log(1/ε)) branching positions. Claim 2: At most extended maximal factors starting at each location. Corollary: each location is in ≤ O((1/ε)2 log(1/ε)) extended maximal factors.

Proof of Lemma 1 2 log(1/ε)) Corollary: each location is in ≤ O((1/ ε ) There are lb starting locations, from each location extended maximalextended factors. maximal factors. there are ≤

Finding Extended Maximal Factors Algorithm for finding extended maximal factors: 1. Transform T to LST(T) 2. Find all maximal factors in LST(T) by: (a) At each starting location try to extend until the prob. drops below ε. (b) Backtrack to previous branching position and try to extend the factor and so on. . . Run time: linear in the output length.

Framework for Solving Weighted Matching Problems: 1. Find all extended maximal factors of T. 2. Concatenate factors (add $’s betw) to get T’. 3. Compute property by extending probabilities until below ε 4. Run property algorithm on text T’ with.

Conclusions • Our framework yields: – Solutions to unsolved weighted matching problems (scaled, swaped, param. matching, indexing) – Efficient solutions to others (exact and approx. ) • For constant ε: – Weighted matching problems can be solved in same running times as regular pattern matching – Weighted ndexing can be solved in same times except for O(n log(n)) preprocessing
 Greedy algorithm
Greedy algorithm Eran (fueron/eran) las doce.
Eran (fueron/eran) las doce. Weighted and non weighted codes
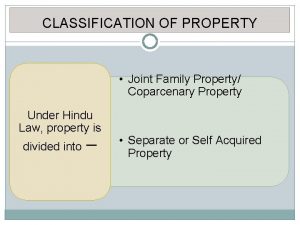
Weighted and non weighted codes Coparcenary property and separate property
Coparcenary property and separate property Chemical properties of citric acid
Chemical properties of citric acid Commutative property vs associative property
Commutative property vs associative property Eran segal
Eran segal Los huilliches eran nómadas o sedentarios
Los huilliches eran nómadas o sedentarios Versiculos de primera comunion
Versiculos de primera comunion Huilliches sedentarios o nómadas
Huilliches sedentarios o nómadas Intentalo fueron/eran las doce
Intentalo fueron/eran las doce Quienes eran los sofistas
Quienes eran los sofistas ¿quiénes eran los juglares?
¿quiénes eran los juglares? Achi brandt
Achi brandt Tnica
Tnica 1 pedro 1 7
1 pedro 1 7 Quiénes eran los francos
Quiénes eran los francos Ubicacion geografica de grecia y roma
Ubicacion geografica de grecia y roma Grecia antigua para secundaria
Grecia antigua para secundaria Ciudades de la edad moderna
Ciudades de la edad moderna Eran tromer
Eran tromer Que era la polis en grecia
Que era la polis en grecia Como se vestian los comechingones
Como se vestian los comechingones Malquesis y quelosis características
Malquesis y quelosis características Cómo eran las uvas que habían en la parra silvestre
Cómo eran las uvas que habían en la parra silvestre Colosense 2 15
Colosense 2 15 Características de atenas
Características de atenas La primera civilizacion
La primera civilizacion Los delfines eran terrestres
Los delfines eran terrestres Yaniv segal
Yaniv segal Que es lo que le agrada a dios
Que es lo que le agrada a dios Hombres que fueron cobardes en la biblia
Hombres que fueron cobardes en la biblia Quienes eran los publicanos
Quienes eran los publicanos