Approximate Online Palindrome Recognition and Applications Amihood Amir









![Sorting by Reversals – Polynomial time Relaxations Signed reversals: Hannenhalli & Pevzner [99] Kaplan, Sorting by Reversals – Polynomial time Relaxations Signed reversals: Hannenhalli & Pevzner [99] Kaplan,](https://slidetodoc.com/presentation_image_h2/45dd9f301787a534b9514f9bfc898275/image-11.jpg)




















- Slides: 40

Approximate On-line Palindrome Recognition, and Applications Amihood Amir Benny Porat

Moskva River

Confluence of 4 Streams Ap pr o xi m at e M at c r hi nd i l a ng e m o c Re P CPM 2014 at a M e g n I ch r e nt ng i h c On line Alg ori t hm s on i t ni g o

Palindrome Recognition - Voz'mi-ka slovo ropot, - govoril Cincinnatu ego shurin, ostriak, -- I prochti obratno. A? Smeshno poluchaetsia? Vladimir Nabokov, Invitation to a Beheading (1) "Take the word ropot [murmur], " Cincinnatus' brother-in-law, the wit, was saying to him, "and read it backwards. Eh? Comes out funny, doesn't it? " [--› topor: the axe] A palindrome is a string that is the same whether read from right to left or from left to right: Examples: доход A man, a plan, a cat, a ham, a yak, a yam, a hat, a canal-Panama!

Palindrome Example Ibn Ezra: Medieval Jewish philosopher, poet, Biblical commentator, and mathematician. Was asked: " "אבי אל חי שמך למה מלך משיח לא יבא [ My Father, the Living God, why does the king messiah not arrive? ] His response: " שוב אליכם כי בא מועד , "דעו מאביכם כי לא בוש אבוש [ Know you from your Father that I will not be delayed. I will return to you when the time will come ]

Palindromes in Computer Science Great programming exercise in CS 101. Example of a problem that can be solved by a RAM in linear time, but not by a 1 -tape Turing machine. (Can be done in linear time by a 2 -tape TM)

Palindrome Concatenation We may be interested in finding out whether a string is a concatenation of palindromes of length > 1. Example: ABCCBABBCCBCAACB Why would we be interested in such a funny problem? – we’ll soon see Exercise: Do this in linear time…

Stream 2 - Approximations As in exact matching, there may be errors. Find the minimum number of errors that, if fixed, will give a string that is a concatenation of palindromes of length > 1 ABCCBABBCCBCAACB Example: ABCCBCBBCCBCABCB For Hamming distance: A-Porat [ISAAC 13]: Algorithm of time O(n 2)

Stream 3 - Reversals Why is this funny problem interesting? Sorting by reversals: In the evolutionary process a substring may “detach” and “reconnect” in reverse: ABCABCDAABCBAD CBAADCB

Sorting by Reversals What is the minimum number of reversals that, when applied to string A, result in string B? History: Introduced: Bafna & Pevzner [95] NP-hard: Carpara [97] Approximations: Christie [98] Berman, Hannenhalli, Karpinski [02] Hartman [03]
![Sorting by Reversals Polynomial time Relaxations Signed reversals Hannenhalli Pevzner 99 Kaplan Sorting by Reversals – Polynomial time Relaxations Signed reversals: Hannenhalli & Pevzner [99] Kaplan,](https://slidetodoc.com/presentation_image_h2/45dd9f301787a534b9514f9bfc898275/image-11.jpg)
Sorting by Reversals – Polynomial time Relaxations Signed reversals: Hannenhalli & Pevzner [99] Kaplan, Shamir, Tarjan [00] Tannier & Sagot [04]. . . Disjointness: Swap Matching Muthu [96] Two constraints: 1. The length of the reversed substring is limited to 2. 2. All swaps are disjoint.

Pattern Matching with Disjoint Reversals • Reversal Distance (RD): – The RD between s 1 and s 2 is the minimum number k, such that there exist s 2’ , where HAM(s 1, s 2’) =k, and s 1 reversal match s 2. S 1: S 2: A D C B A E D B A A D A A B C E RD(S 1, S 2) = 2

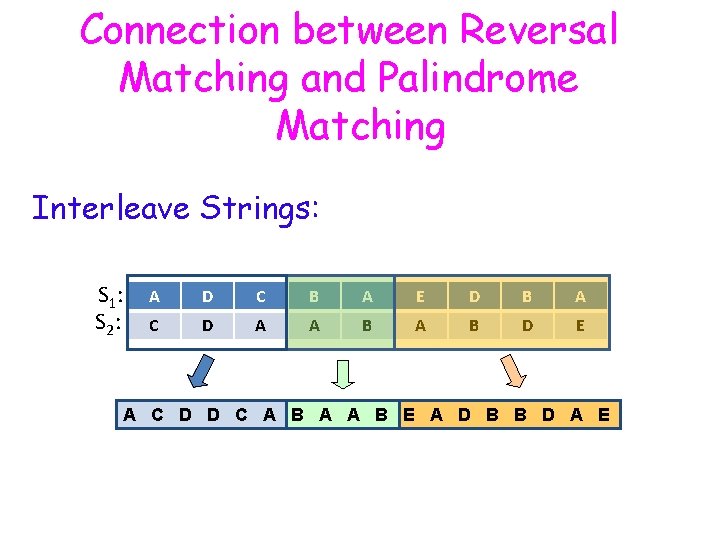
Connection between Reversal Matching and Palindrome Matching Interleave Strings: S 1: S 2: A D C B A E D B A C D A A B D E A C D D C A B A A B E A D B B D A E

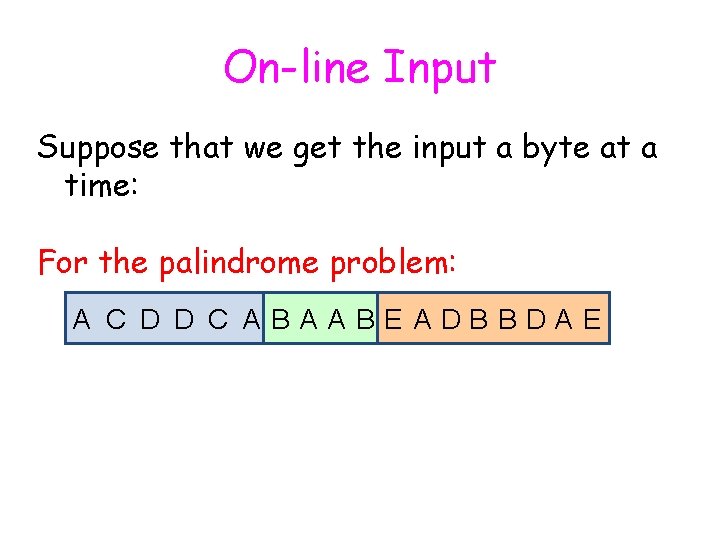
On-line Input Suppose that we get the input a byte at a time: For the palindrome problem: A C D D C ABAABEADBBDAE

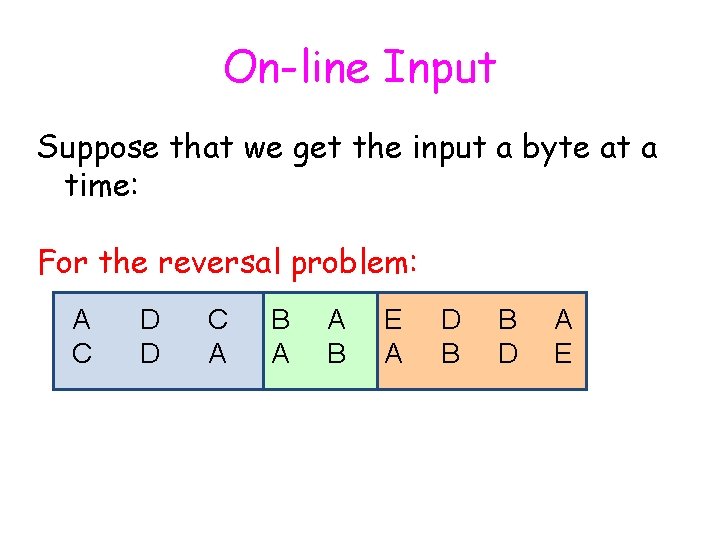
On-line Input Suppose that we get the input a byte at a time: For the reversal problem: A C D D C A B A A B E A D B B D A E

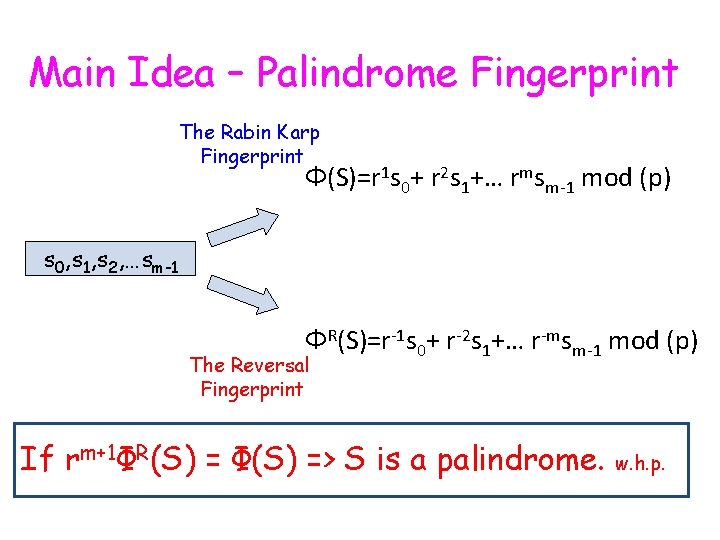
Main Idea – Palindrome Fingerprint The Rabin Karp Fingerprint Φ(S)=r 1 s 0+ r 2 s 1+… rmsm-1 mod (p) s 0, s 1, s 2, …sm-1 ΦR(S)=r-1 s 0+ r-2 s 1+… r-msm-1 mod (p) The Reversal Fingerprint If rm+1ΦR(S) = Φ(S) => S is a palindrome. w. h. p.

Palindrome Fingerprint If rm+1ΦR(S) = Φ(S) => S is a palindrome. Φ(S)=r 1 s 0+ r 2 s 1+… rmsm-1 mod (p) Example: r 6ΦR(S)=r-1 s 0+ r-2 s 1+… r-msm-1 mod (p) S=ABCBA r 6 (1/r A + 1/r 2 B + 1/r 3 C + 1/r 4 B + 1/r 5 A) = r 5 A + r 4 B + r 3 C + r 2 B + r A = Φ(S)

Simple Online Algorithm for Finding a Palindrome in a Text t 1, t 2, t 3, … ti, ti+1, ti+2 , …ti+m, ti+m+1 , … tn Φ=r 1 ti+ r 2 ti+1+… rmti+m mod (p) If rm+1ΦR =Φ => ΦR=r-1 ti+ r-2 ti+1+… r-mti+m mod (p) there is a palindrome starting in the i-th position. If not, then for the next position: Φ= Φ + rm+1 t i+m+1 mod (p) ΦR=ΦR + r-(m+1)ti+m+1 mod (p) Note: This algorithm finds online whether the prefix of a text is a permutation. For finding online whether the text is a concatenation of permutations, assume even-length permutations, otherwise, every text is a concatenation of length-1 permutations.

Palindrome with mismatches Start with 1 mismatch case.

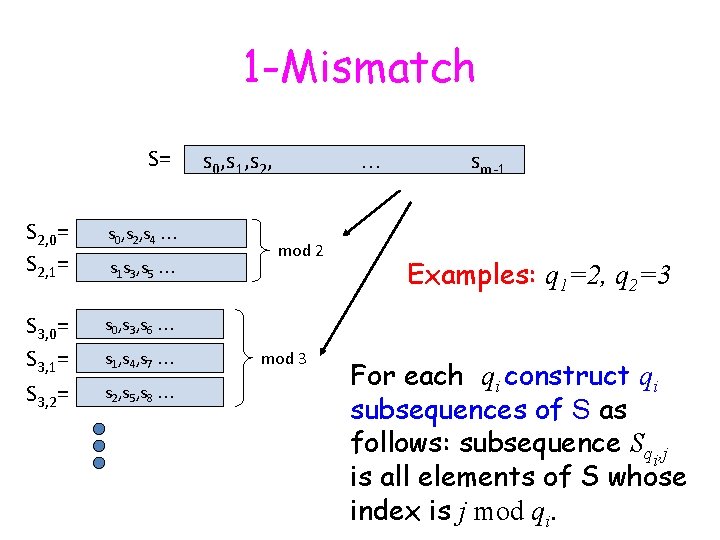
1 -Mismatch S= s 0, s 1, s 2, … sm-1 Choose l prime numbers q 1, …, ql < m such that

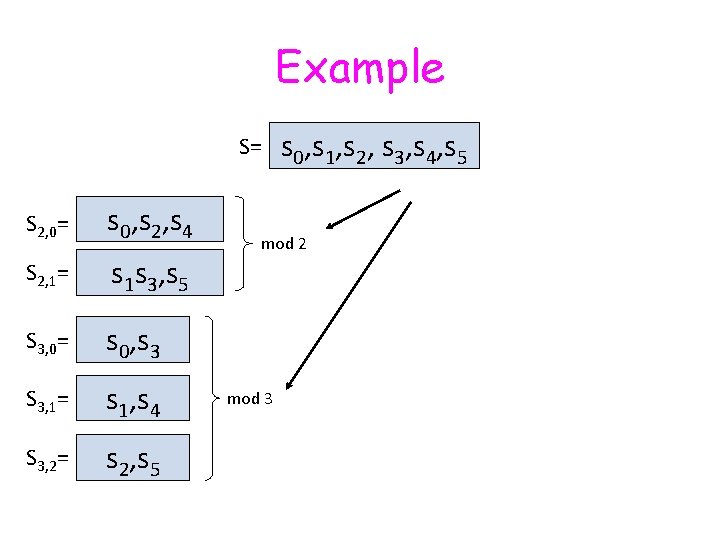
1 -Mismatch S= S 2, 0= S 2, 1= s 0, s 2, s 4 … S 3, 0= S 3, 1= S 3, 2= s 0, s 3, s 6 … s 1 s 3, s 5 … s 1, s 4, s 7 … s 2, s 5, s 8 … s 0, s 1, s 2, … mod 2 mod 3 sm-1 Examples: q 1=2, q 2=3 For each qi construct qi subsequences of S as follows: subsequence Sqi, j is all elements of S whose index is j mod qi.

Example S= S 2, 0= s 0, s 2, s 4 S 2, 1= s 1 s 3, s 5 S 3, 0= s 0, s 3 S 3, 1= s 1, s 4 S 3, 2= s 2, s 5 s 0, s 1, s 2, s 3, s 4, s 5 mod 2 mod 3

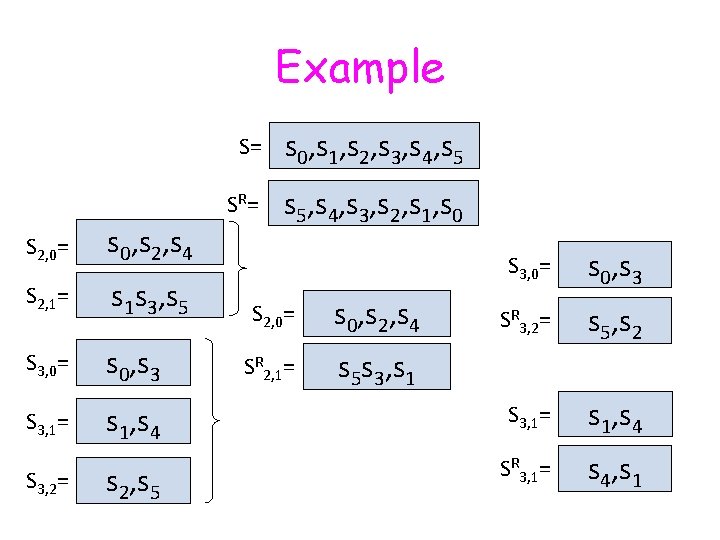
1 -Mismatch • We need to compare: s 0 , s 1 , s 2 , sm-1, sm-2, sm-3 … sm-2 , sm-1 … s 1 , s 0 • We prove that in the partitions strings: Sq, j= SRq, (m-1 -j)mod q

Example S 2, 0= s 0, s 2, s 4 S 2, 1= s 1 s 3, s 5 S 3, 0= s 0, s 3 S 3, 1= S 3, 2= S= s 0, s 1, s 2, s 3, s 4, s 5 SR = s 5, s 4, s 3, s 2, s 1, s 0 S 3, 0= s 0, s 3 SR 3, 2= s 5, s 2 s 1, s 4 S 3, 1= s 1, s 4 s 2, s 5 SR 3, 1= s 4, s 1 S 2, 0= s 0, s 2, s 4 SR 2, 1= s 5 s 3, s 1

Exact Matching Lemma: S=SR Sq, j = SRq, (m-1 -j) mod for all q and all 0 ≤ j ≤ q. q

1 -Mismatch Lemma: There is exactly one mismatch There is exactly one subpattern in each group that does not match. C. R. T

Chinese Remainder Theorem Let n and m two positive integers. In our case: if two different indices, i and j, have an error, and only one subsequence is erroneous, since the product of all q’s > m, it means that i=j.

Complexity There exists a constant c such that, for any x<m, there at least x/log m prime numbers between x and cx. Therefore, choose prime numbers between log m and c log m.

Complexity • For each qi we compute 2 qi different fingerprints: • Overall space: • Each character participates in exactly two fingerprints (the regular and the reverse). • Overall time:

Online All fingerprint calculations can be done online We know the m at every input character, to compute the comparisons. Conclude: Our algorithm is online.

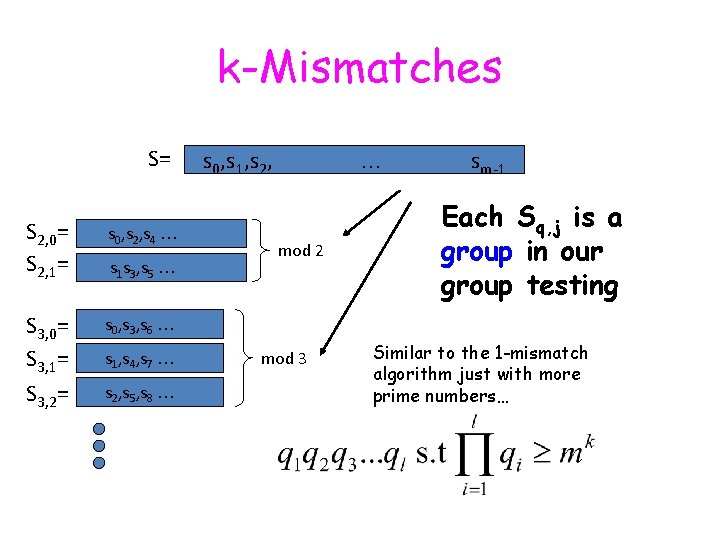
k-Mismatches Use Group testing…

k-Mismatches Group Testing • Given n items with some positive ones, identify all positive ones by a small number of tests. • Each test is on a subset of items. • Test outcome is positive iff there is a positive item in the subset.

k-Mismatch • Group: partition of the text. • Test: distinguish between: algorithm) – match – 1 -mismatch – more then 1 -mismatch (using the 1 -mismatch

k-Mismatches S= S 2, 0= S 2, 1= s 0, s 2, s 4 … S 3, 0= S 3, 1= S 3, 2= s 0, s 3, s 6 … s 1 s 3, s 5 … s 1, s 4, s 7 … s 2, s 5, s 8 … s 0, s 1, s 2, … mod 2 mod 3 sm-1 Each Sq, j is a group in our group testing Similar to the 1 -mismatch algorithm just with more prime numbers…

Our tests • We define The reversal pair of Sq, j to be SRq, (m-1 -j)mod q • Each partition is “tested against” its reversal pair.

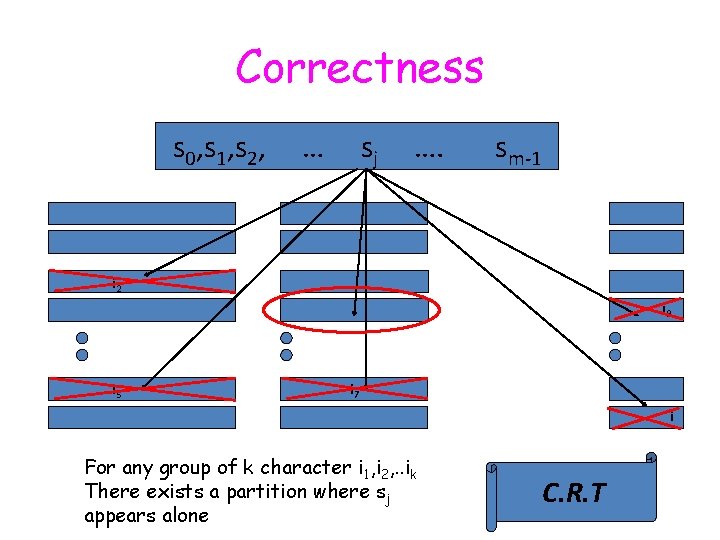
Correctness s 0, s 1, s 2, … sj …. sm-1 i 2 i 9 i 5 i 7 i For any group of k character i 1, i 2, . . ik There exists a partition where sj appears alone C. R. T

Correctness s 0, s 1, s 2, … sj …. sm-1 i 2 i 9 i 5 i 7 i If sj invokes a mismatch we will catch it.

Complexity • Overall space: • Overall time:

Approximate Reversal Distance Using the palindrome up to k-mismatches algorithm, can be solved in time, and space.

 Greedy algorithm
Greedy algorithm Nucleotide nomenclature
Nucleotide nomenclature Regular expression for palindrome
Regular expression for palindrome Palindrome quiz
Palindrome quiz Ei.cfg
Ei.cfg Palindrome c++
Palindrome c++ A grammar g=(vtps) in which v represents
A grammar g=(vtps) in which v represents Palindrome words
Palindrome words Palindrome
Palindrome Mga halimbawa ng tulang diyamante
Mga halimbawa ng tulang diyamante Gcd vs gcf
Gcd vs gcf Ict content tools
Ict content tools Fast exact and approximate geodesics on meshes
Fast exact and approximate geodesics on meshes Cv nnn
Cv nnn Megabyte
Megabyte Approximate computing
Approximate computing Board ga,e
Board ga,e Short poem about module
Short poem about module Musical periods
Musical periods What are musical devices in poetry
What are musical devices in poetry A building bent deflects in the same way as
A building bent deflects in the same way as A guided tour to approximate string matching
A guided tour to approximate string matching Approximate computing
Approximate computing Approximate counting algorithm
Approximate counting algorithm Fourteen billion years represents the approximate age of
Fourteen billion years represents the approximate age of Type line and pattern area
Type line and pattern area Lshzoo
Lshzoo How to approximate the best fitting line for data
How to approximate the best fitting line for data Approximate symmetrical balance
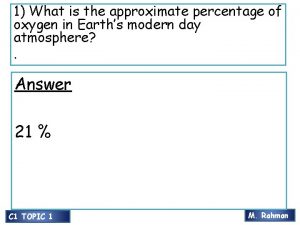
Approximate symmetrical balance What is the approximate percentage of oxygen in the air?
What is the approximate percentage of oxygen in the air? Sketch techniques for approximate query processing
Sketch techniques for approximate query processing Approximate cell decomposition
Approximate cell decomposition What does this map represent
What does this map represent Refrain figurative language
Refrain figurative language Collector emitter loop
Collector emitter loop Times are approximate
Times are approximate A guided tour to approximate string matching
A guided tour to approximate string matching Recognition and regard for oneself and one's abilities: *
Recognition and regard for oneself and one's abilities: * Where did pritilata fight
Where did pritilata fight Amir tokic
Amir tokic Amir abdala
Amir abdala