Amihood Amir Avivit Levy Ely Porat and B

Amihood Amir, Avivit Levy, Ely Porat and B. Riva Shalom CPM 2014 1 DICTIONARY MATCHING WITH ONE GAP

CPM 2014 - MOSCOW CPM 2014 2

MIND THE GAP! CPM 2014 3

OUTLINE The CPM 2014 DMG(Dictionary Matching with one Gap ) Problem Motivation Previous Work Bidirectional Suffix Trees Solution Lookup Table addition Open Problems 4

THE DMG PROBLEM CPM 2014 A gapped pattern is a pattern P of the form: P 1{ 1, 1} P 2{ 2, 2}… Pk-1{ k-1, k-1}Pk Each Pj is over alphabet , { j, j} is a sequence of at least j and at most j don’t cares = @. Example: aba{3, 6}cbb aba @@@cbb aba@@@@@cbb aba@@@@@@cbb 5

THE DMG PROBLEM The DMG problem is: Preprocess: A dictionary D of d gapped CPM 2014 patterns P 1, …, Pd over alphabet . Query: A text T of length n over alphabet . Output: all locations in T where a dictionary gapped pattern ends. We focus on DMG with a single gap. 6

EXAMPLE Query text: CPM 2014 Dictionary: P 1 = aba {3, 6} cbb P 2 = ab {3, 6} bbac P 3 = aa {3, 6} ac 1 2 3 4 5 6 7 8 9 10 11 abaabacbbac P 1, 1 P 2, 1 P 3, 1 P 1, 2 P 2, 2 P 3, 2 First =1≤i≤d{ Pi, 1 } Second=1≤i≤d{ Pi, 2 } 7

MOTIVATION Computational CPM 2014 Biology A renew interest due to cyber security. Network intrusion detection systems perform protocol analysis, content searching and content matching to detect harmful software. Malware may appear in several packets! 8

PREVIOUS WORK Gapped CPM 2014 pattern matching problem was studied for a few decades, eg. [Myers, JACM 1992], [Navaro&Raffinot, Algorithmica 2004], [Bille&Thorup, ICALP 2009] , [Bille&Thorup SODA 2010], [Morgante et al. , JCB 2005], [Rahman et al. , COCOON 2006], [Bille et al. , TCS 2012] DMG problem not studied enough ! [Kucherov&Rosinovich, TCS 1997], [Zhang et al. , IPL 2010]-no bounds on the length of the gap. 9

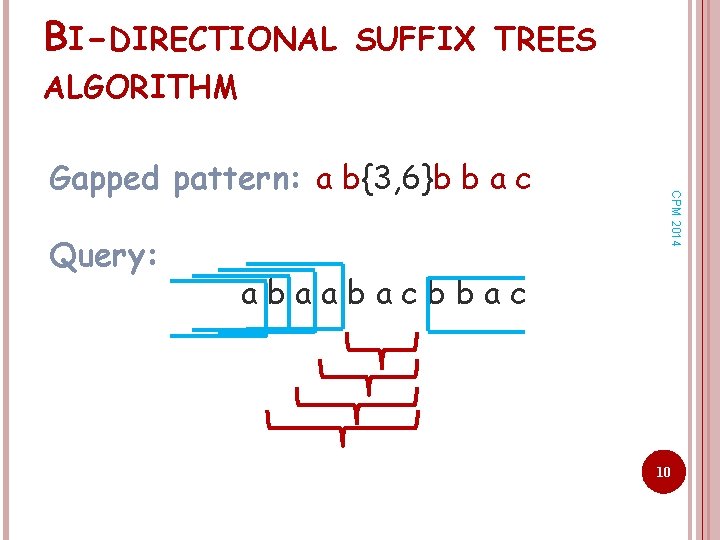
BI-DIRECTIONAL SUFFIX TREES ALGORITHM Query: CPM 2014 Gapped pattern: a b{3, 6}b b a c abaabacbbac 10

BI-DIRECTIONAL SUFFIX TREES ALGORITHM Idea: view as [Amir et al. , JAL 2000] Use suffix tree TFR of First. R CPM 2014 Gapped patterns: P 1= a b a{3, 6}a b a c P 2= a b a{3, 6}b b a P 3= a b{3, 6}b a a Query: abaabacbbac gap Use suffix tree TS of 11 Second

BI-DIRECTIONAL SUFFIX TREES ALGORITHM Finds Pi, 2 starting at location l. CPM 2014 For each text location l Insert tl tl +1…tn to TS (the node h) to find labels on the path to h. For f= l - -1 to l - -1 Insert tftf-1…t 1 to TFR (the node g) to find labels on the path to g. Finds Pi, 1 ending at location f. Output intersection (for end locations). 12

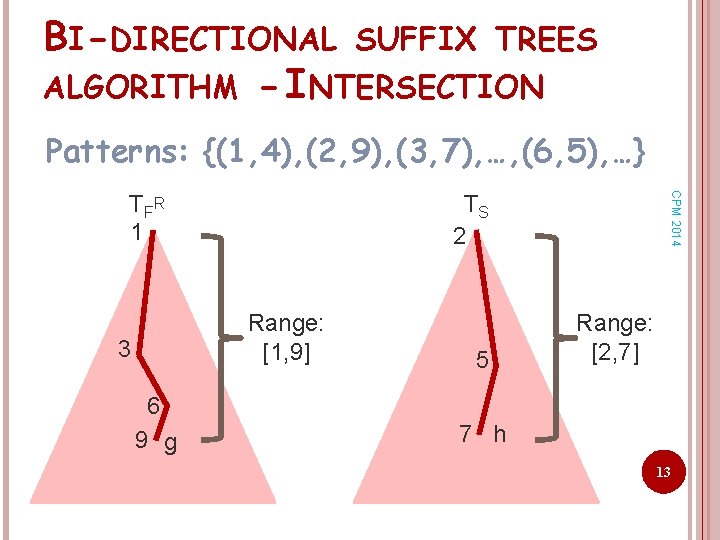
BI-DIRECTIONAL SUFFIX TREES ALGORITHM - INTERSECTION Patterns: {(1, 4), (2, 9), (3, 7), …, (6, 5), …} TS 2 Range: [1, 9] 3 6 9 g CPM 2014 T FR 1 5 Range: [2, 7] 7 h 13

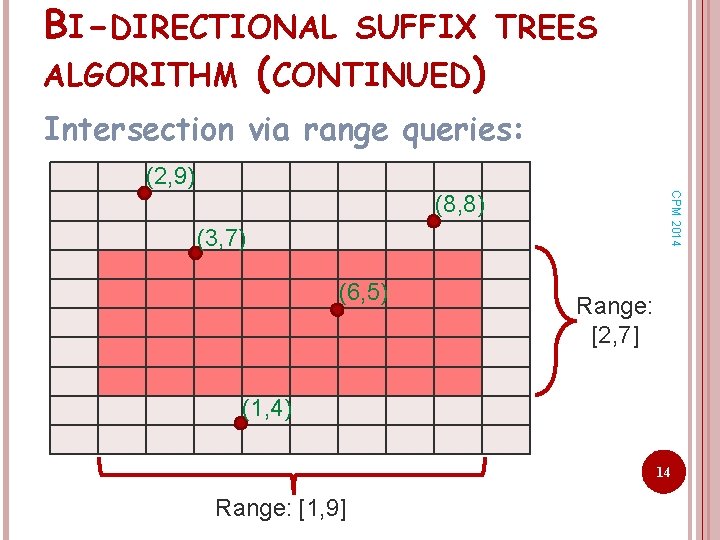
BI-DIRECTIONAL SUFFIX TREES ALGORITHM (CONTINUED) Intersection via range queries: (2, 9) CPM 2014 (8, 8) (3, 7) (6, 5) Range: [2, 7] (1, 4) 14 Range: [1, 9]

TIME & SPACE Preprocessing Time: Dictionary segments suffix tree and reverse suffix tree: O(|D|) Preprocessing grid for range queries: O(d log d). [Chan et al. , So. CG 2011] CPM 2014 Preprocessing Space: Dictionary segments suffix tree and reverse suffix tree: O(|D|) Space for grid: O(d log d). [Chan et al. , So. CG 2011] 15

TIME & SPACE Query Time: For each end text location, we try every gap size: a factor of . The number of range queries is the number of vertical paths in a given path: 1 O(log 2 min{d, log |D|}). A range query costs: O(log d+occ). 3 CPM 2014 [Chan et al. , So. CG 2011] Total: O(n( )log d log 2 min{d, log |D|}+occ). 6 9 g 16

LOOKUP TABLE ALGORITHM CPM 2014 Idea: Instead of using range queries in a grid to compute the intersection, we use a pre-computed lookup table. Enables intersection in O(occ) time. Total query time becomes: O(n( )+occ). 17

LOOKUP TABLE ALGORITHM CPM 2014 Inter[g, h] = all i s. t. Pi, 1 R appears on the path from the root of TFR till node g and Pi, 2 appears on the path from the root of TS till node h. Inter[ 3, 5 ]= {4} P 1=(1, 4), P 2=(2, 9), P 3=(3, 7), P 4=(3, 2), …, P 6=(6, 5), P 7 =(9, 6) 1 3 g 6 9 2 5 h 7 18

LOOKUP TABLE ALGORITHM CPM 2014 Inter[g, h] = all i s. t. Pi, 1 R appears on the path from the root of TFR till node g and Pi, 2 appears on the path from the root of TS till node h. Inter[ 3, 5 ]= {4} Inter[ 3, 7 ]= {3, 4} P 1=(1, 4), P 2=(2, 9), P 3=(3, 7), P 4=(3, 2), …, P 6=(6, 5), P 7 =(9, 6) 1 3 g 6 9 2 5 7 h 19

LOOKUP TABLE ALGORITHM CPM 2014 Inter[g, h] = all i s. t. Pi, 1 R appears on the path from the root of TFR till node g and Pi, 2 appears on the path from the root of TS till node h. Inter[ 3, 5 ]= {4} Inter[ 3, 7 ]= {3, 4} Inter[ 6, 7 ]= {3, 4, 6} P 1=(1, 4), P 2=(2, 9), P 3=(3, 7), P 4=(3, 2), …, P 6=(6, 5), P 7 =(9, 6) 1 3 g 6 9 2 5 7 h 20

LOOKUP TABLE ALGORITHM CPM 2014 Inter[g, h] = all i s. t. Pi, 1 R appears on the path from the root of TFR till node g and Pi, 2 appears on the path from the root of TS till node h. Inter[ 3, 5 ]= {4} Inter[ 3, 7 ]= {3, 4} Inter[ 6, 7 ]= {3, 4, 6} Inter[ 9, 7 ]= {3, 4, 6} P 1=(1, 4), P 2=(2, 9), P 3=(3, 7), P 4=(3, 2), …, P 6=(6, 5), P 7 =(9, 6) 1 3 6 9 g 2 5 7 h 21

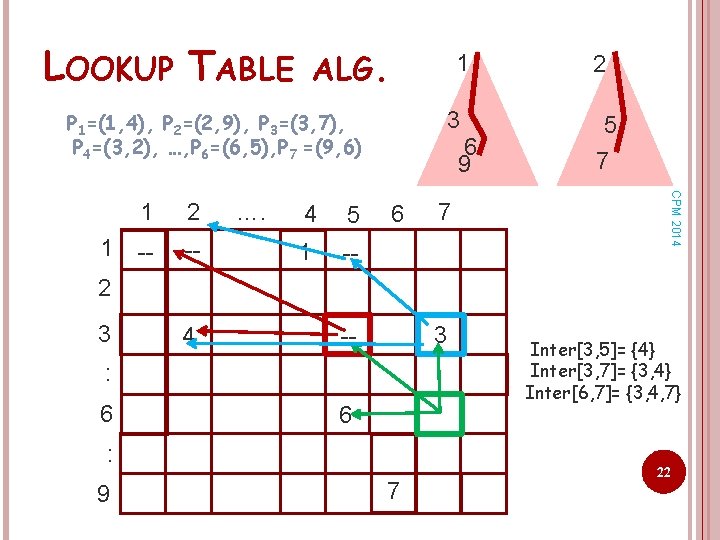
LOOKUP TABLE ALG. 1 3 P 1=(1, 4), P 2=(2, 9), P 3=(3, 7), P 4=(3, 2), …, P 6=(6, 5), P 7 =(9, 6) 2 -- -- …. 4 5 1 -- 6 7 5 7 CPM 2014 1 1 6 9 2 2 3 4 3 -- : 6 6 : 9 7 Inter[3, 5]= {4} Inter[3, 7]= {3, 4} Inter[6, 7]= {3, 4, 7} 22

LOOKUP TABLE ALGORITHM CPM 2014 Preprocessing: Time: Table can be computed using DP in time O(d 2 ovr + |D|) where ovr is the number of subpatterns including other subpattern as a prefix or suffix. Space: O(d 2 + |D|). Query time: O(n( )+occ). 23

CPM 2014 Bi-directional suffix trees & OUR RESULTS range queries Preprocessing time: O(d log d + |D|). Space: O(d log d + |D|). Query time: O(n( )log d log 2(min{d, log |D|} )+occ). Bi-directional suffix trees & Lookup table Preprocessing time: O(d 2 ovr + |D|). Space: O(d 2 + |D|). 24 Query time: O(n( )+occ).

OPEN PROBLEMS to k gaps Reducing the dependency on the size Scalability to different gap bounds in the dictionary Online algorithm CPM 2014 Generalizing 25

CPM 2014 26