Function Matching Amihood Amir Yonatan Aumann Moshe Lewenstein

Function Matching Amihood Amir Yonatan Aumann Moshe Lewenstein Ely Porat Bar Ilan University

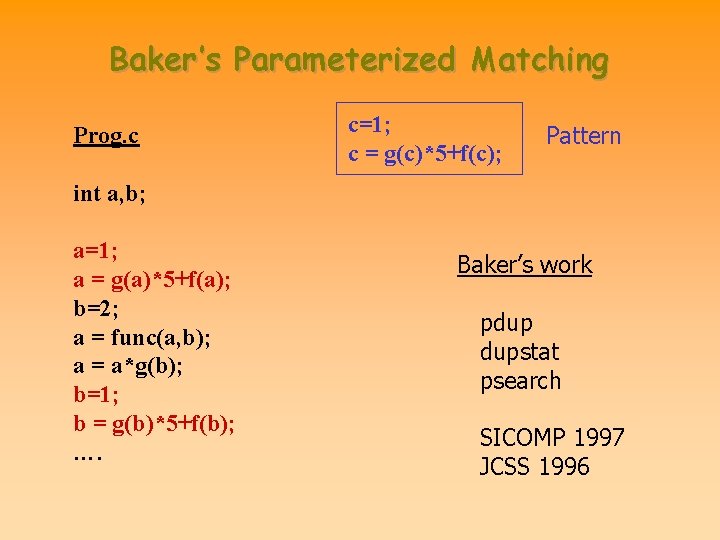
Baker’s Parameterized Matching Prog. c int a, b; a=1; a = g(a)*5+f(a); b=2; a = func(a, b); a = a*g(b); b=1; b = g(b)*5+f(b); ….

Baker’s Parameterized Matching Prog. c c=1; c = g(c)*5+f(c); Pattern int a, b; a=1; a = g(a)*5+f(a); b=2; a = func(a, b); a = a*g(b); b=1; b = g(b)*5+f(b); …. Baker’s work pdup dupstat psearch SICOMP 1997 JCSS 1996

Two dimensional parameterized matching pattern ‘A horse is a horse, it ain’t make a difference what color it is’ John Wayne

Parameterized Matching Input P = p 1…pm T = t 1. . . tn Output: over alphabet locations i of T, for which a bijection : exists s. t. (P) = (p 1) (p 2)… (pm) = ti…ti+m-1

Parameterized Matching • One dimensional • Baker 1996, JCSS • Baker 1997, SICOMP • Amir, Farach, Muthu 1995, IPL • Two dimensional Regular methods fail !! - Suffix Trees - Boyer Moore - Knuth-Morris-Pratt

Function Matching Input: P = p 1…pm T = t 1. . . tn Output: over alphabet locations i of T, where f: f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 exists s. t.

Function Matching Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 P=hehaeh T=abcbacbadabdaddad exists s. t.

Function Matching Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: exists f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 P= hehaeh T=abcbacbadabdaddad f(h) = b f(e) = c f(a) = a s. t.

Function Matching Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: exists f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 P= hehaeh T=abcbacbadabdaddad f(h) = a f(e) = d f(a) = b s. t.

Function Matching Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: exists f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 P= hehaeh T=abcbacbadabdaddad f(h) = d f(e) = a f(a) = d s. t.

Function Matching Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: exists f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1 no match ! P= hehaeh T=abcbacbadabdaddad f(h) = ? ? s. t.

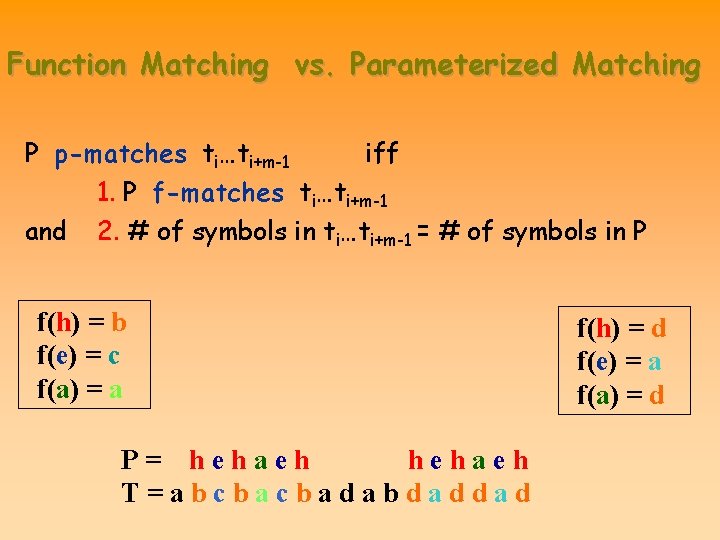
Function Matching vs. Parameterized Matching P p-matches ti…ti+m-1 and iff 1. P f-matches ti…ti+m-1 2. # of symbols in ti…ti+m-1 = # of symbols in P f(h) = b f(e) = c f(a) = a P= hehaeh T=abcbacbadabdaddad f(h) = d f(e) = a f(a) = d

Naïve Algorithm At each location i of text T check if pattern f-matches Check For each letter ‘a’ in pattern Are elements aligned with the pattern ‘a’s the same? no? declare ‘no match’ All letters “OK” – declare ‘match’ Running time: O(nm), where m = |P| and n = |T|

Function Matching with Don’t Cares Input: P = p 1…pm over alphabet T = t 1. . . tn over alphabet Output: locations i of T, where f: f(P) = f(p 1)f(p 2)…f(pm) = ti…ti+m-1, f(? ) - wildcard P= he? ? eh T=abcbacbcdbcdaddad {? } exists s. t.

Why do we need don’t cares? Pattern Text

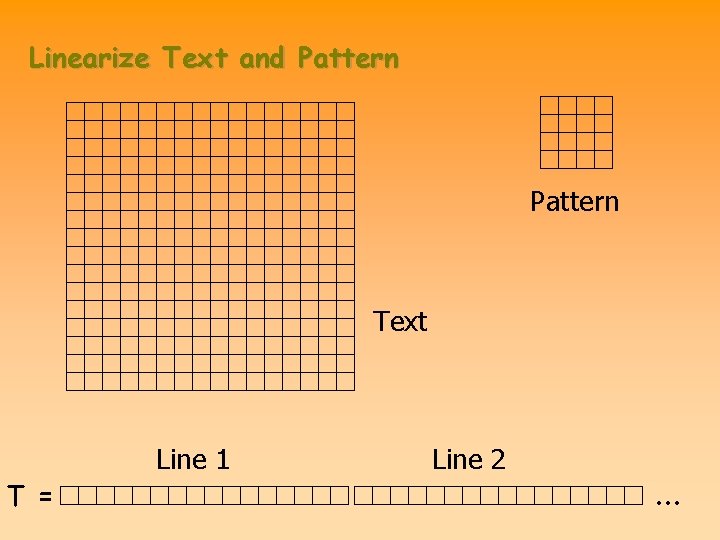
Linearize Text and Pattern Text Line 1 T = Line 2 …

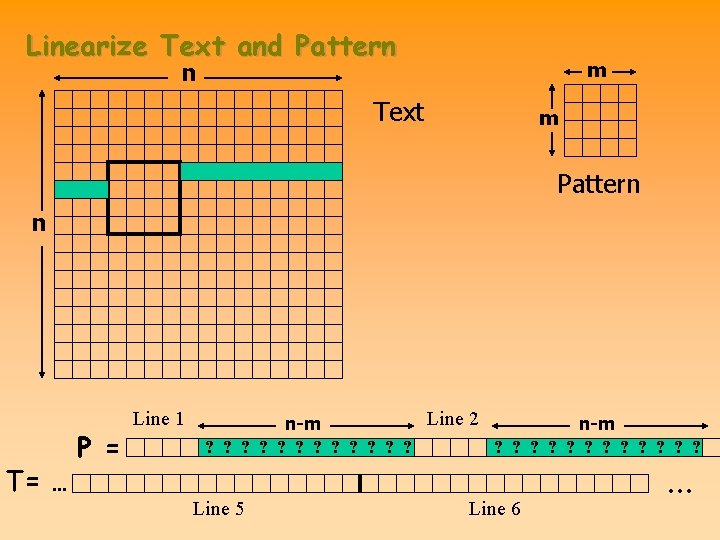
Linearize Text and Pattern n m Text m Pattern n T= … P = Line 1 Line 2 n-m ? ? ? ? ? ? Line 5 Line 6 …

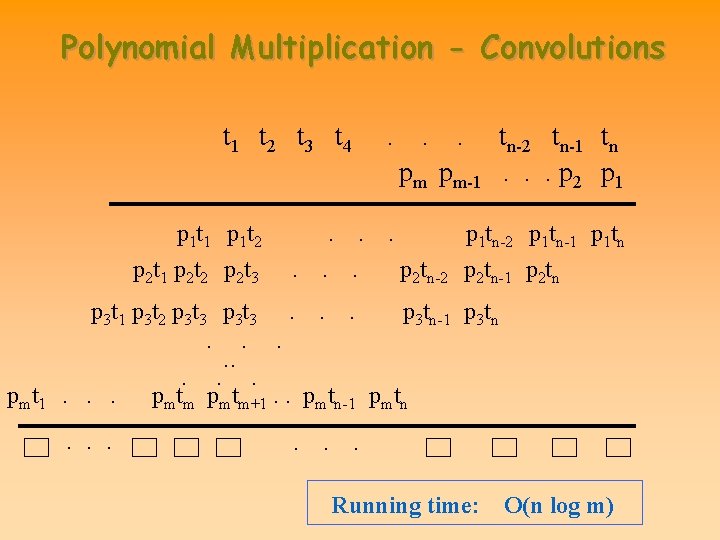
Polynomial Multiplication - Convolutions t 1 t 2 t 3 t 4 . . . pm pm-1 p 1 t 2 p 2 t 1 p 2 t 2 p 2 t 3 . . . p 3 t 1 p 3 t 2 p 3 t 3 . . . pmt 1. . . p 2 tn-2 tn-1 tn. . . p 2 p 1 tn-2 p 1 tn-1 p 1 tn p 2 tn-1 p 2 tn p 3 tn-1 p 3 tn . pmtm+1. . pmtn-1 pmtn. . . Running time: O(n log m)

Convolutions: Fischer-Patterson [1974] p 1 p 2 p 3 p 4. . . pm t 1 t 2 t 3 t 4. . . tn-2 tn-1 tn pm pm-1. . . p 2 p 1 t 1 p 1 t 2 p 2 t 1 p 2 t 2 p 2 t 3 . . . p 3 t 1 p 3 t 2 p 3 t 3 p 3 t 4 . . . pmt 1. . . . p 2 tn-2 p 3 tn-1 p 3 tn pmtm+1. . pmtn-1 pmtn. . . p 1 tn-2 p 1 tn-1 p 1 tn p 2 tn-1 p 2 tn

Convolutions: Fischer-Patterson [1974] p 1 p 2 p 3 p 4. . . pm t 1 t 2 t 3 t 4. . . tn-2 tn-1 tn pm pm-1. . . p 2 p 1 t 1 p 1 t 2 p 2 t 1 p 2 t 2 p 2 t 3 . . . p 3 t 1 p 3 t 2 p 3 t 3 p 3 t 4 . . . pmt 1. . . p 2 tn-2 . p 3 tn-1 p 3 tn . pmtm+1. . pmtn-1 pmtn. . p 1 tn-2 p 1 tn-1 p 1 tn p 2 tn-1 p 2 tn .

How does this help for Function Matching? The property that needs to be checked is: beneath each symbol from the pattern alphabet all text characters must be the same

Example T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h

Example T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h h in P vs. a in T Ta = 1 0 0 0 1 0 1 0 0 1 P Rh = 00100101

Example T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h h-a Ta = 1 0 0 0 1 0 1 0 0 1 P Rh = 00100101 1000100101001001001 0000000000000000000 10001001001001 0000000000000000000 00100111020210301201201101

Example hehaeh? e T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h h-a Ta = 1 0 0 0 1 0 1 0 0 1 P Rh = 00100101 1000100101001001001 0000000000000000000 10001001001001 0000000000000000000 00100111020210301201201101

Example T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h h-a Ta = 1 0 0 0 1 0 1 0 0 1 P Rh = 00100101 00100111020210301201201101 => in O(n log m) time!!

Example T=abcbacbacabdaddadea P=hehaeh? e PR = e ? h e a h e h h-a h-b h-c 102021030120 030111101010 201201101000 h-d 000000101203 Match(h) 01000001 => in O(| | n log m) time!!

In general - the Algorithm • For each character ‘a’ in create P a • For each character ‘b’ in create T b • For all Pa and Tb multiply them and construct Match(a) for each ‘a’ in • Announce each location i of T as a ‘match’ if Match(a)[i] = 1 for all a’s in P => in O(| || | n log m) time.

Improvement Lemma: Let a 1, . . . , ak , then k iff for all i, j, ai = aj Idea: Let’s encode text with numbers for symbols and encode pattern to compute their sum and separately their sum of squares.

Improvement Lemma: Let a 1, . . . , ak , then k iff for all i, j, ai = aj Example: Compute sum of text char’s beneath “e” T# = 1 2 3 2 1 3 1 2 4 1 4 5 1 T = a b c b a c a b d a d e a P = h e h a e h ? e Pe = 0 1 0 0 1

Improvement Lemma: Let a 1, . . . , ak , then k iff for all i, j, ai = aj Example: Compute sum of squares beneath “e” T#2= 1 4 9 4 1 T# = 1 2 3 2 1 T = a b c b a P = h e h a e Pe = 0 1 0 0 1 9 4 1 9 1 4 16 1 16 25 1 3 2 1 3 1 2 4 1 4 5 1 c b a c a b d a d e a h ? e 0 0 1

Improvement Lemma: Let a 1, . . . , ak , then k iff for all i, j, ai = aj Running Time: Two convolutions for each pattern character. O(| | n log m)

We have seen – 2 algorithms for Function Matching 1. O(nm) 2. O(| - naïve algorithm | n log m) - convolution based Can we do better for big alphabets? 1. O(n log 2 m) 2. Lower bound of We will see: - randomized convolutions based (nm) for deterministic convolutions based methods

Def: A pattern is 2 -charactered if every character appears at most twice in the pattern. Lemma: Let P be a pattern and T a text. 2 -charactered patterns P 1 and P 2 s. t. at loc. i of T P f-matches iff P 1 and P 2 f-match. Example: P = a b c c b b P 1 = a 1 b 1 c 1 c 2 b 2 (even pairs) P 2 = a 1 b 1 c 1 b 2 c 2 b 3 (odd pairs)

Situation: An algorithm for Function Matching with 2 -charactered patterns a general algorithm for Function Matching. So, all that needs to be checked is that: each pair in P has equal text symbols beneath it.

New Randomized Algorithm 1. For each character: - a in T, randomly choose ra in {0, 1} - relace all a’s in T with ra - get T’ - b in P, randomly choose sb in {1, 2} - set first b to be sb and the second b to be -sb - get P’ 2. Convolve T’ and P’R 3. For each location i, for which T’*P’R[i] equals 0 for the convolution declare a ‘match’

Example: P=vqvuqu? s T=abaababacabdabcbdba h(v) = a h(q) = b h(u) = a h(s) = a g(P) = 2 6 – 2 8 – 6 – 8 0 0 f(T) = 1 0 1 0 1 0 1 1 0 0 0 1 2+0– 2+8+0– 8+0+0 = 0 g(v) = 2 g(q) = 6 g(u) = 8 f(a) f(b) f(c) f(d) = = 1 0 0 1

Example: P= vqvuqu? s T=abaababacabdabcbdba g(P) = 2 6 – 2 8 – 6 – 8 0 0 f(T) = 1 0 1 0 1 0 1 1 0 0 0 1 0+6– 2+0 -6+0+0+0 = -2 g(v) = 2 g(q) = 6 g(u) = 8 f(a) f(b) f(c) f(d) = = 1 0 0 1

Example: P= vqvuqu? s T=abaababacabdabcbdba g(P) = 2 6 – 2 8 – 6 – 8 0 0 f(T) = 1 0 1 0 1 0 1 1 0 0 0 1 0= 2+6+0+0+0 -8+0+0 g(v) = 2 g(q) = 6 g(u) = 8 f(a) f(b) f(c) f(d) = = 1 0 0 1

Running Time: O(nk log m) with probability 2 -k O(n log 2 m) with probability 1/m Correctness: if P f-matches at location i of T then f(T)*g(P)R [i+m-1] is trivially always equal to 0 if P does not f-match at location i of T then for each convolution <f, g>, f(T)*g(P)R [i+m-1], equals 0 with probability ½ with k rounds of amplification the probability is (½)k

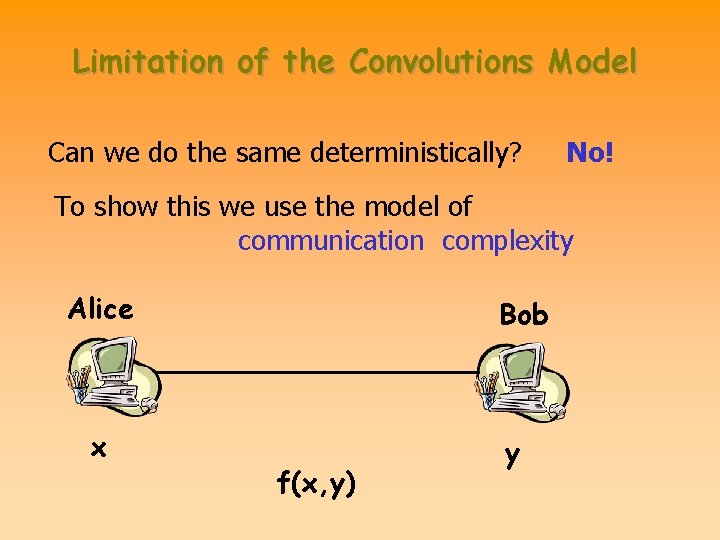
Limitation of the Convolutions Model Can we do the same deterministically? No! To show this we use the model of communication complexity Alice x Bob f(x, y) y

Limitation of the Convolutions Model Known: for x, y in {0, 1}k the communication complexity of equals(x, y) is (k) Take pattern P = a 1 a 2 a 3 … am, where i j ai aj Given a collection of convolutions {<g(P), f(T)>} the convolutions of location i, (g(P)*f(t))[i+m-1] = g(aj )*f(ti+j-1) + g(aj )*f(ti+j+m-1). Since we are in essence comparing ti…ti+m-1 to ti+m…ti+2 m-1 we get the equal information from the convolution. This is lower bounded by (m) for each location, In general (nm)

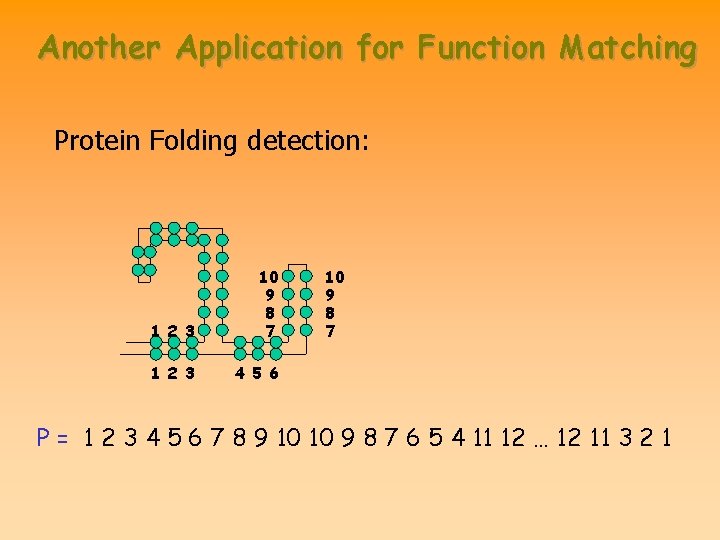
Another Application for Function Matching Protein Folding detection: 1 2 3 10 9 8 7 1 2 3 4 5 6 10 9 8 7 P = 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 11 12 … 12 11 3 2 1

Questions 1. Can Function Matching be solved deterministically in o(nm) time for big alphabets? 2. Are there special cases of Function Matching that are easier (other than Parameterized Matching and other trivial ones)? 3. Does 2 -dimensional Parameterized Matching need to be solved with function matching?