Ponte di Paderno sullAdda Localit Paderno Calusco LC

Ponte di Paderno sull’Adda Località Paderno – Calusco (LC) d to u l a s o r o a c i c m n a U o u t l a e l e u m a S Pinti Luca Via Signoria, 64 06089 Torgiano (PG)

LA NOSTRA PRESENTAZIONE: Dopo aver ricevuto dal mio amico Samuele la cartolina illustrata precedentemente, ho pensato di utilizzarla come modello di funzione quadratica per la partecipazione al progetto “Matematica e Realtà”.

LA GEOMETRIA E IL PONTE DI PADERNO D’ADDA Sezione

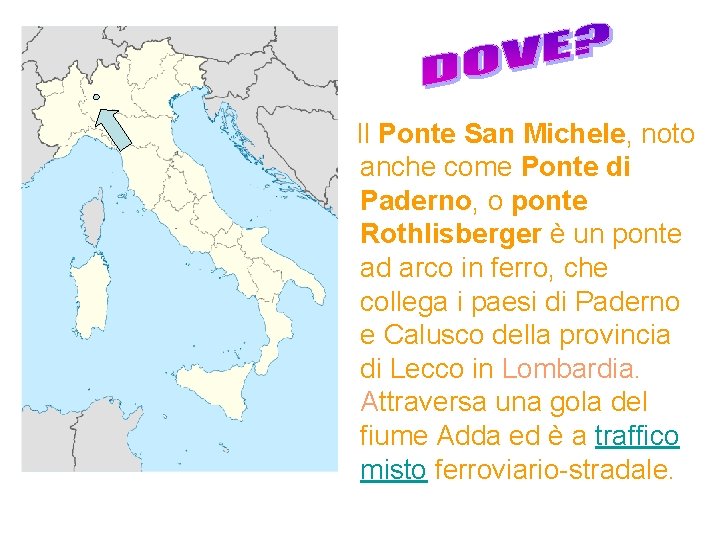
Il Ponte San Michele, noto anche come Ponte di Paderno, o ponte Rothlisberger è un ponte ad arco in ferro, che collega i paesi di Paderno e Calusco della provincia di Lecco in Lombardia. Attraversa una gola del fiume Adda ed è a traffico misto ferroviario-stradale.

Il ponte venne costruito tra il 1887 e il 1889 per diventare uno dei pochi collegamenti ferroviari tra l'est e l'ovest dell'Adda. Vennero concordati soli diciotto mesi per il completamento dell'opera, in seguito furono fatte piccole modifiche al progetto originale, allungando ed elevando il ponte alle misure attuali (cinque metri in più di corda dell'arco, 42 in più di lunghezza). La costruzione venne terminata nel marzo 1889; nel maggio dello stesso anno venne effettuato il collaudo.

Il ponte, progettato dall'ingegnere svizzero Jules Röthlisberger (18511911), è lungo 266 metri, e si eleva a 85 metri al di sopra del livello del fiume. Ha una duplice funzione perché nella parte superiore è strada provinciale, mentre 6 m sotto corre la ferrovia. Il ponte è sostenuto da 9 appoggi, quattro dei quali poggiano su una grande arcata metallica formata da un primo arco parabolico di 150 m di corda e 37, 50 m di freccia sormontato da un altro arco parabolico che ha dal primo distanza minima di 5 m e distanza massima di 8 m.

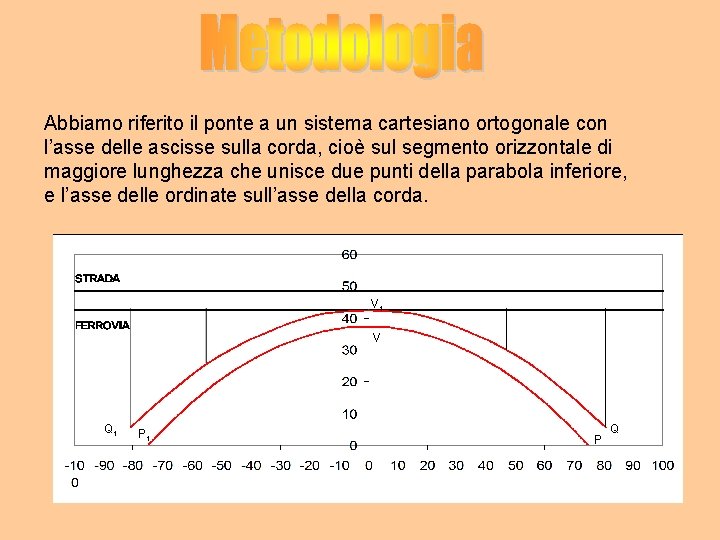
Abbiamo riferito il ponte a un sistema cartesiano ortogonale con l’asse delle ascisse sulla corda, cioè sul segmento orizzontale di maggiore lunghezza che unisce due punti della parabola inferiore, e l’asse delle ordinate sull’asse della corda. V 1 V Q 1 P Q

Abbiamo determinato le equazioni della strada superiore e della ferrovia e le equazioni dei due archi parabolici. Equazione Ferrovia : retta parallela all’asse delle x h = 37, 50 m + 5 m y = 42, 5 (y=h) con – 133 ≤ x ≤ 133 Equazione Strada provinciale : retta parallela all’asse delle x ( y = k) k = 37, 50 m + 5 m + 6 m y = 48, 5 con -133 ≤ x ≤ 133 Equazione dell’arco parabolico inferiore : parabola con asse di simmetria 2 l’asse delle y ( y = ax + c ) Gli estremi dell’ arco sono P( 75; 0) e P 1(-75; 0) La parabola ha vertice V 1 (0; 37, 5) e passa per P(75; 0) da cui y=- x 2 + 37, 5 con -75 ≤ x ≤ 75

Equazione dell’arco parabolico superiore : è una parabola con asse di 2 simmetria l’asse delle y y = ax + c Il secondo arco ha i due estremi sulle normali alla parabola del primo arco condotte per P e per 1 P a una distanza di 8 m da entrambi punti. Per determinare l’ equazione della tangente in P alla prima parabola abbiamo risolto il seguente sistema: retta tangente in P: y = - x + 75 Abbiamo determinato l’equazione della normale in P alla prima parabola: y = x – 75 Abbiamo determinato le coordinate del punto Q di questa normale che dista da P 8 m: Q ( 75 + 4 ; 4 ) circa Q ( 80, 66; 5, 66 ) Abbiamo determinato le coordinate dell’altro estremo Q 1 del secondo arco parabolico : Q 1 ( - 75 - 4 ; 4 ) circa Q ( - 80, 66; 5, 66 ) La parabola del secondo arco ha vertice V 2 ( 0 ; 42, 5 ) e passa per Q ( 75 + 4 ; 4 ) 2 La sua equazione è: y = -0, 00566 x +42, 5 -80, 66≤ x ≤+80, 66

l L’equazione delle funzioni utilizzate nello studio del ponte sono state: 1. 2. 3. 4. y = 42, 5 y = 48, 5 y = -1/150 x 2 + 37, 5 y = -0, 00566 x 2 +42, 5 equazione ferrovia equazione della strada equazione del 1° arco parabolico del ponte equazione del 2° arco parabolico del ponte

Basta guardarsi intorno per constatare che, dall’oggetto più insignificante al meccanismo più sofisticato, tutto è realizzato servendosi di qualche branca della matematica e che come diceva Pitagora “tutto è numero” e come diceva Platone “tutto è forma”.

Istituto Tecnico Statale Commerciale e per Geometri “Ruggero Bonghi” – Assisi CECCUCCI DANIELE PEPSINI SARA COLLIRONI MARTINA SCARPONI FEDERICA FAMIANI FRANCESCA TIMI ANNA MARIA MANTOVANI MARCO TRUMA JULIANA APOSTOLICO NICOLA PINTI LUCA PROF. SSE: TINI ILIANA e MALIZIA ARCANGELA