POLINOMIOS U D 5 4 ESO E AP

POLINOMIOS U. D. 5 * 4º ESO E. AP. @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 1

DIVISIÓN POR RUFFINI U. D. 5. 5 * 4º ESO E. AP. @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 2

Regla de Ruffini • REGLA DE RUFFINI • • • Cuando se trate de dividir un polinomio P(x) entre un binomio de la forma (x - a), siendo a un número, la división de puede realizar de una forma más rápida y precisa: • • 1. ‑ Se reduce el dividendo. 2. ‑ Se ordena el dividendo forma decreciente. 3. ‑ Si el dividendo es incompleto, poner ceros. 4. ‑ Se colocan en fila los coeficientes del dividendo, incluidos los ceros. 5. - Se coloca a la izquierda el valor del número a. 6. - Se aplicar el algoritmo correspondiente de Ruffini. 7. ‑ Los números obtenidos son los coeficientes del cociente, salvo el último que es el resto de la división. 8. - Se puede comprobar el resultado, pues siempre se cumplirá: D(x) = d(x). c(x) + r(x). • • @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 3

Ejemplo_1 de división por Ruffini • Sea ( x 3 + 4. x 2 - 5 ) : ( x - 3 ) , donde a = 3 • • • 3 1 • • 4 0 -5 3 21 63 7 21 58 + C(x) = 1. x 2 + 7. x + 21 R(x) = 58 Podemos comprobar la división: (x 3 + 4. x 2 - 5) = (x - 3). (x 2 + 7. x + 21) + 58 @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 4

Ejemplo_2 de división por Ruffini • Sea ( x 3 + 4. x 2 - 5 ) : ( x + 5 ) , donde a = - 5 • 1 • • -5 • • • 1 4 0 -5 + -5 5 - 25 -1 5 - 30 C(x) = 1. x 2 - 1. x + 5 R(x) = - 30 Podemos comprobar la división: (x 3 + 4. x 2 - 5) = (x + 5 ). (x 2 - x + 5) + (- 30) @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 5

Ejemplo_3 de división por Ruffini • Sea ( 4. x 3 + 5. x - 3 ) : ( x + 2 ) , donde a = - 2 • 4 • • -2 • • • 4 0 5 -3 + -8 16 - 42 -8 21 - 45 C(x) = 4. x 2 - 8. x + 21 R(x) = - 45 Podemos comprobar la división: ( 4. x 3 + 5. x - 3 ) = ( x + 2 ). (4. x 2 - 8. x + 21) + (- 45) @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 6

Método escalonado de Ruffini • Sea P(x) = x 3 – 3 x 2 + 3. x – 1 dividido entre Q(x) = (x – 1) • • Como P(x) es una potencia notable, sabemos que: P(x) = (x – 1)3 = (x – 1) • Luego al dividir P(x) entre (x – 1) la división será exacta y el resto 0. • • Podemos poner: D(x) = d(x). C(x) (x – 1)3 = (x – 1). (x 2 – 2. x + 1) • • • Seguimos dividiendo por Ruffini, ahora C(x) : (x – 1) Y tendremos C(x) = (x – 1) Con lo cual: (x – 1)3 = (x – 1) • Este método escalonado se emplea para hallar las raíces o ceros de un polinomio; o lo que es lo mismo, para resolver ecuaciones de grado superior a 3 como veremos en los apartados siguientes. @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 7

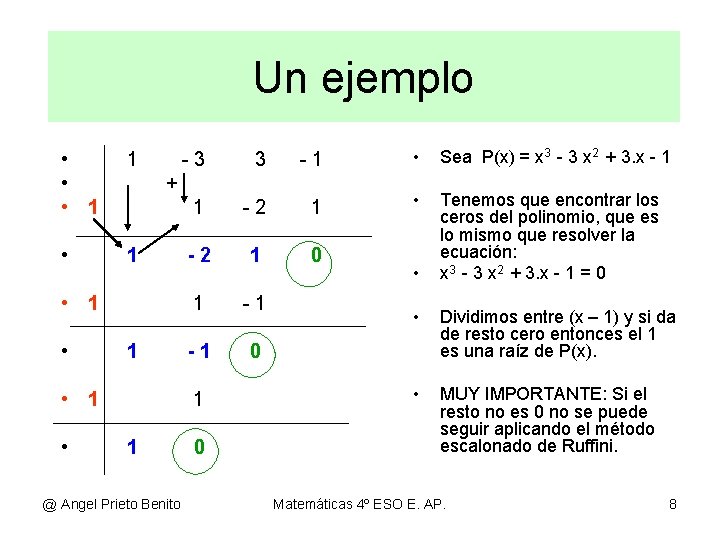
Un ejemplo • • • 1 1 • 1 • 3 -1 • Sea P(x) = x 3 - 3 x 2 + 3. x - 1 1 -2 1 • -2 1 0 Tenemos que encontrar los ceros del polinomio, que es lo mismo que resolver la ecuación: x 3 - 3 x 2 + 3. x - 1 = 0 1 -1 -1 0 + • 1 • -3 1 1 @ Angel Prieto Benito 0 • • Dividimos entre (x – 1) y si da de resto cero entonces el 1 es una raíz de P(x). • MUY IMPORTANTE: Si el resto no es 0 no se puede seguir aplicando el método escalonado de Ruffini. Matemáticas 4º ESO E. AP. 8

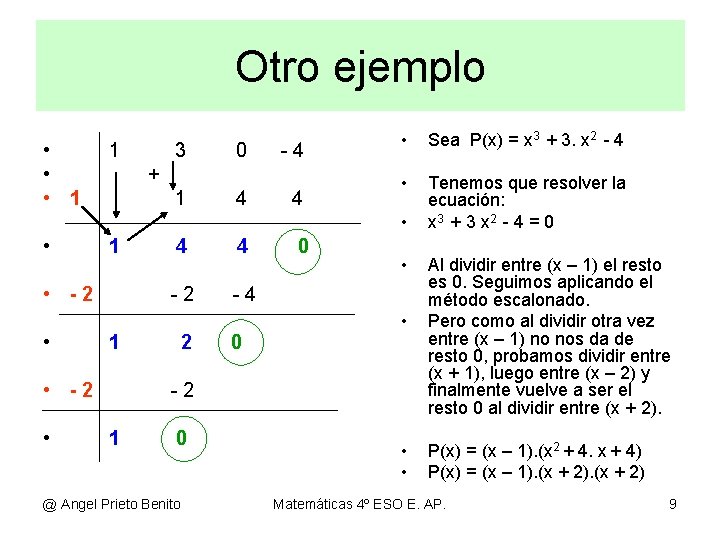
Otro ejemplo • • • 1 1 3 0 -4 + 1 4 4 • Sea P(x) = x 3 + 3. x 2 - 4 • Tenemos que resolver la ecuación: x 3 + 3 x 2 - 4 = 0 • • 1 • -2 • 4 -2 -4 1 • -2 • 4 2 0 0 • • -2 1 0 @ Angel Prieto Benito • • Al dividir entre (x – 1) el resto es 0. Seguimos aplicando el método escalonado. Pero como al dividir otra vez entre (x – 1) no nos da de resto 0, probamos dividir entre (x + 1), luego entre (x – 2) y finalmente vuelve a ser el resto 0 al dividir entre (x + 2). P(x) = (x – 1). (x 2 + 4. x + 4) P(x) = (x – 1). (x + 2) Matemáticas 4º ESO E. AP. 9