PLANIMETRIE Mgr Martina Fainov POZNMKY ve formtu PDF

PLANIMETRIE Mgr. Martina Fainová POZNÁMKY ve formátu PDF TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČR

Metrické pojmy v rovině metrické = měřitelné, tj. určování vzdáleností a odchylek Vzdálenost bodu M od přímky p = vzdálenost bodu M od paty kolmice vedené bodem M k přímce p M značení: v(M, p) = |MP| p ● Poznámka: M p v(M, p) = 0 P P - pata kolmice

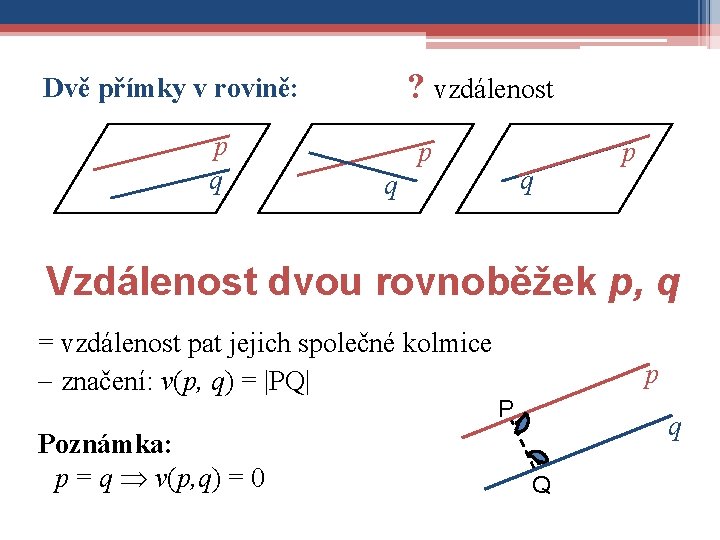
? vzdálenost Dvě přímky v rovině: p q p p q q Vzdálenost dvou rovnoběžek p, q = vzdálenost pat jejich společné kolmice značení: v(p, q) = |PQ| P q ● Poznámka: p = q v(p, q) = 0 p ● Q

Odchylka dvou přímek = velikost ostrého nebo pravého úhlu, který přímky svírají značení: = | p, q| p p q q ? Poznámka: 1) Odchylka dvou rovnoběžných nebo splývajících přímek je 0. 2) Odchylka dvou různoběžek je vždy úhel z (0 ; 90 ) 3) Odchylka kolmých přímek je 90. Průsečík kolmice s danou přímkou se nazývá pata kolmice.

Cvičení: Příklad 1: Je dán čtverec ABCD o hraně 4 cm. a) Určete vzdálenost bodu A od přímky CD. b) Určete vzdálenost bodu C od přímky BD. c) Určete odchylku úhlopříček. Příklad 2: Je dán kosočtverec ABCD s hranou a a úhlem při vrcholu A o velikosti 55. a) Určete vzdálenost přímek AB a CD. b) Určete odchylku přímek AB a AD. Příklad 3: V rovnostranném trojúhelníku ABC s hranou a. Určete vzdálenost vrcholu C od přímky AB.

Množina bodů dané vlastnosti = geometrický útvar, jehož body mají stejnou vlastnost Množina všech bodů, které mají od daného pevného bodu S danou vzdálenost r je kružnice. Poznámka: Tato kružnice je také množinou všech středů kružnic, které mají daný poloměr a procházejí daným S. Množina všech bodů, které mají od dvou daných bodů AB stejnou vzdálenost je osa úsečky AB. Poznámka: Tato osa je také množinou všech středů kružnic, které procházejí danými body A, B.

Množina bodů dané vlastnosti Množina všech bodů, které mají od přímky p danou vzdálenost r, jsou dvě přímky p 1, p 2 , rovnoběžné s p a ležící v opačných polorovinách. Poznámka: Tyto rovnoběžky jsou také množinou všech středů kružnic, které mají daný poloměr a dotýkají se p. Množina všech bodů, které mají od dvou daných rovnoběžek stej. vzdálenost je osa pásu jimi omez. . Poznámka: Tato osa je také množinou všech středů kružnic, které se dotýkají daných rovnoběžek.

Množina bodů dané vlastnosti Množina všech bodů, které mají stej. vzdálenost od dvou různoběžek a, b jsou přímky o 1 o 2 , které určují osy úhlů sevřených různoběžkami. Poznámka: Tyto osy jsou také množinou všech středů kružnic, které se dotýkají přímek a, b. Množina všech bodů, z nichž je vidět úsečka AB pod úhlem 90 je Thaletova kružnice. Poznámka: Thaletova kružnice je kružnice sestrojená nad průměrem AB.

Cvičení: Příklad 1: Je dána přímka p a bod A, který na ní neleží. Určete množinu středů všech úseček AX, X p. přímka q||p, |Aq|=|qp| Příklad 2: Určete množinu všech středů úseček, které mají krajní body na dvou různých rovnoběžkách a, b. přímka p||a, |ap|=|pb| Příklad 3: Určete množinu bodů, které mají od daného bodu A vzdálenost menší nebo rovnu 3 cm. kruh se středem S a poloměrem 3 cm