Kvadratick nerovnice Mgr Martina Fainov POZNMKY ve formtu

Kvadratické nerovnice Mgr. Martina Fainová POZNÁMKY ve formátu PDF TENTO PROJEKT JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČR

Kvadratická nerovnice Kvadratickou nerovnicí o jedné neznámé je každá nerovnice, kterou lze ekvivalentními úpravami převést na jeden z tvarů ax 2 + bx + c < 0, ax 2 + bx + c > 0, ax 2 + bx + c 0, kde a, b, c R a a 0. - využijeme znalostí kvadratické funkce, kvadratické rovnice a řešení nerovnic v podílovém tvaru

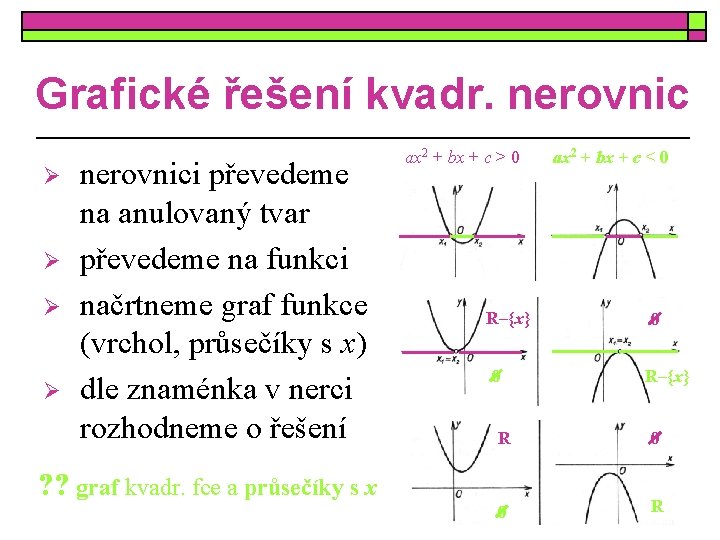
Grafické řešení kvadr. nerovnic Ø Ø nerovnici převedeme na anulovaný tvar převedeme na funkci načrtneme graf funkce (vrchol, průsečíky s x) dle znaménka v nerci rozhodneme o řešení ax 2 + bx + c > 0 R–{x} 0 ax 2 + bx + c < 0 0 R–{x} R 0 0 R ? ? graf kvadr. fce a průsečíky s x

Příklad: Graficky řešte nerovnici x 2 + 3 x + 3 2 x + 9. Řešení: V: x 2 + 3 x + 3 2 x + 9 x 2 + x – 6 0 f: y = x 2 + x – 6 f průsečíky s x: x 2 + x – 6 = 0 x 1 = -3 K = (-∞; -3 2; ∞) P 1[-3; 0] x 2 = 2 P 2[2; 0]

Cvičení: Příklad 1: Graficky řešte dané nerovnice v R: a) 13 x 15 > 2 x 2 e) x 2 + 2 x 3 > 0 b) x 2 2 x + 1 0 f) 6 x 2 x 2 4, 5 c) x 2 + 2 x > -6 g) (x – 2)(2 x + 7) < 0 d) 0, 5 x 2 + 1, 5 x h) (2 x + 1)2 < 0 Příklad 2: Rozložte dané kvadratické trojčleny na součin lineárních členů: c) 9 + 3 x 2 – 4 x a) 5 x 2 – 4 x – 12 d) 4 x 2 + 4 x + 1 b) 2 a 2 – 5 a – 7

Početní řešení kvadr. nerovnic Ø nerovnici převedeme na anulovaný tvar Ø najdeme kořeny odpovídající kvadr. rovnice v D > 0 x 1; x 2 rozložíme kvadr. trojčlen nerovnice v součinovém tvaru v D = 0 x nerce má jedno, nebo žádné řešení v D < 0 nerovnice nemá řešení nerovnice má řešení nebo nemá žádné (dosadíme lib. číslo - např. 0 a dle pravdivosti získané nerovnosti rozhodneme o řešení)

Nerovnice v součinovém tvaru r např. (x + 1)(2 x + 3) > 0 r řešíme podobně jako nerovnice v podílovém tvaru

Příklad 1: V R řešte nerovnici – 2 x 2 + 13 x > 15. Řešení: – 2 x 2 + 13 x > 15 – 2 x 2 + 13 x – 15 > 0 – 2 x 2 + 13 x – 15 = 0 : (– 2) x 1 = 0 x 2 = 5

Příklad 2: V R řešte nerovnice a) x 2 – 2 x + 1 0 b) 0, 5 x 2 – x + 1, 5 > 0 Řešení: a) x 2 – 2 x + 1 0 x 2 – 2 x + 1 = 0 (x – 1)2 0 0 x– 1=0 x=1 K = {1} b) 0, 5 x 2 – x + 1, 5 > 0 x=1 0, 5 x 2 – x + 1, 5 = 0 D = -2 NEPLATÍ, že nerce nemá řešení zvolíme lib. x: x = 0 0, 5 02 – 0 + 1, 5 = 1, 5 > 0 K=R

Cvičení: Příklad 1: Řešte dané nerovnice v R: a) x 2 4 0 e) 13 x 15 > 2 x 2 b) x 2 + 4 x < 0 f) x 2 2 x + 1 0 c) (x 2)(x + 1) > 0 g) x 2 + 2 x > -6 d) 2(x + 3)(x 0, 5) > 0 h) 0, 5 x 2 + 1, 5 x Příklad 2: Určete, pro která čísla x platí, že jeho druhá mocnina je menší než číslo samo. Příklad 3: Určete, pro která čísla platí, že jeho 2. mocnina je větší než dvojnásobek zmenšený o 2.