Physics 121 Electricity and Magnetism Lecture 15 E

Physics 121 - Electricity and Magnetism Lecture 15 E - AC Circuits & Resonance II No Y&F reference for slides on Complex analysis • Circuit Analysis using Complex Exponentials – – Imaginary and Complex Numbers Complex Exponential Phasors and Rotations Phasors as Solutions of Steady State Oscillator Equations Phasor representation applied to current versus voltage in R. L. C. – Series LCR Circuit using Complex Phasors – Parallel LCR Circuit using Complex Phasors – Transient Solution of Damped Oscillator using Complex Phasors Copyright R. Janow – Fall 2015

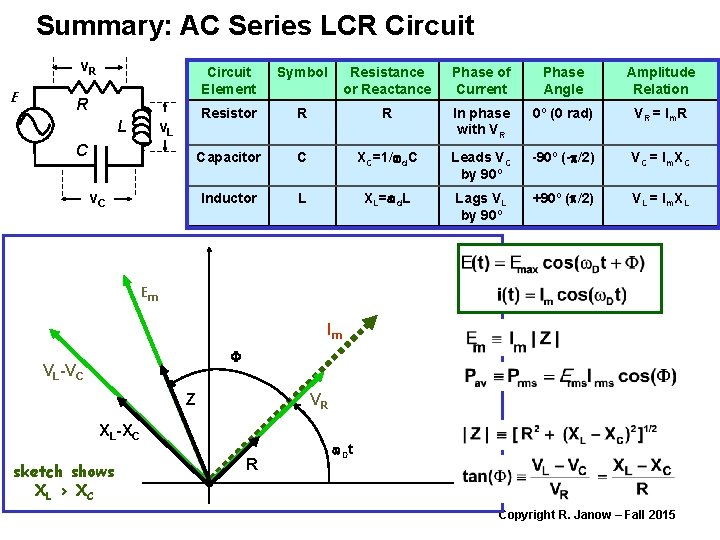
Summary: AC Series LCR Circuit v. R E R L v. L C v. C Circuit Element Symbol Resistance or Reactance Phase of Current Phase Angle Amplitude Relation Resistor R R In phase with VR 0º (0 rad) VR = Im R Capacitor C XC=1/wd. C Leads VC by 90º -90º (-p/2) VC = Im XC Inductor L XL=wd. L Lags VL by 90º +90º (p/2) VL = Im XL Em Im F VL-VC Z VR XL-XC sketch shows XL > X C R w. Dt Copyright R. Janow – Fall 2015

Complex Exponentials in Circuit Analysis is “pure imaginary” • Roots of a quadratic equation az 2 + bz +c = 0 are complex if b 2<4 ac: • Complex number in rectangular form: REVERSE SIGN OF IMAGINARY PART • Re{z} and Im{z} are both real numbers • Complex conjugate: • Addition: • EE’s use j instead of i (i is for current) Copyright R. Janow – Fall 2015

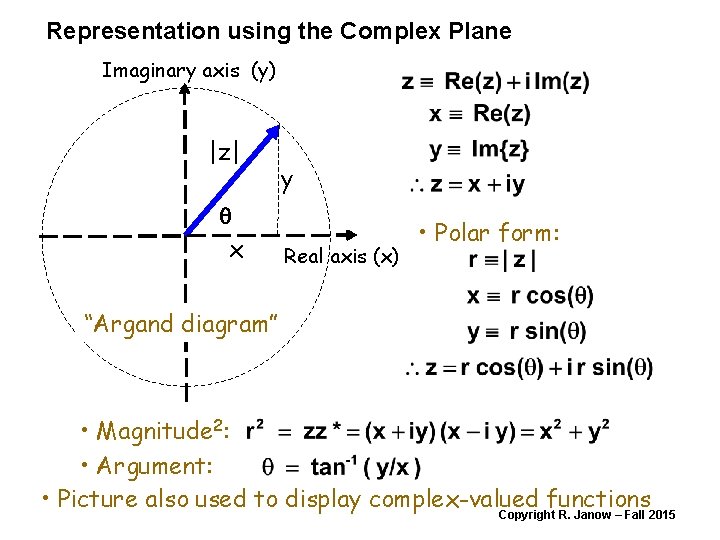
Representation using the Complex Plane Imaginary axis (y) |z| q x y Real axis (x) • Polar form: “Argand diagram” • Magnitude 2: • Argument: • Picture also used to display complex-valued functions Copyright R. Janow – Fall 2015

Complex Exponentials: Euler’s Formula • Taylor’s Series definition of exponential function: • Evaluate with u = iq: use i 2 n+1 = i(-1)2 n • The real & imaginary parts are series for sine and cosine: • Hence: Above is a complex number of magnitude 1, argument q: • Special Properties: Copyright R. Janow – Fall 2015

Rules for Complex Quantities Euler’s Formula with magnitude r: Polar form of arbitrary complex z Complex conjugate of z Sum: Product: • Magnitude of a product = product of individual magnitudes • Argument of a product = sum of individual arguments • Two complex entities are equal if and only if their amplitudes (magnitudes) are equal and their arguments (phases) are equal Periodicity 2 p: De. Moivre’s Theorem: for integer n & k = 0, 1…. n-1 Copyright R. Janow – Fall 2015

Phasors, Rotation Operators, Evolution Operators: e+if rotates complex number z by angle +f in complex plane Im +f Time Evolution: Let f = w(t-t 0) q -f Re evolves z from t 0 to tf for tf > t 0 Represent sinusoidally varying real quantity a(t) as a vector in the complex plane, rotating (counterclockwise) at angular frequency w. • • A(t) is called a “time domain phasor” Re {A(t)} is the measurable instantaneous value of A(t) Time dependent exponentials like eiwt are sometimes called evolution operators Cancelling common factors of eiwt leaves a “frequency domain phasor” A (often simply called a “phasor”): Copyright R. Janow – Fall 2015

Phasor Definitions, continued A phasor represents a sinusoidal, steady state signal whose amplitude Amax, phase f, and frequency w are time invariant. peak value of a(t), real instantaneous value, time domain, real time domain phasor, complex frequency domain phasor A, complex, rotated by f from real axis Phasor Transform Operator P: Forward - time to frequency domain: Inverse - frequency to time domain: Advantage of phasor transform: For sinusoidal signals, differential equations (in the time domain) become algebraic equations (in the frequency domain) as common factors of eiwt cancel). Process: Replace real variables in time dependent analysis problem with variables written using complex exponentials. Cancel common factors of eiwt and solve remaining algebraic problem. Then return to real solution in time domain. Copyright R. Janow – Fall 2015

Time domain phasors are alternative solutions to sines and cosines in differential equations representing oscillations. Recall: chain rule: a can be complex First and Second Derivatives: set a = wt+f, amplitude Amax Example: Simple Harmonic Oscillator Trig Solutions: Complex Solutions: Copyright R. Janow – Fall 2015

Complex Exponential Representation applied to Passive Circuit Elements: Revisit AC Voltage vs. Current in L, C, and R Apply complex voltage & current (time domain phasors): Resistor: Note: now using j = sqrt(-1) i(t) v R( t ) magnitudes: exponents: Inductor: i(t) magnitudes: L exponents: v. L(t) Capacitor: i(t) magnitudes: exponents: C v. C ( t ) Copyright R. Janow – Fall 2015

Summary: Complex Exponential Representation of AC Voltage vs. Current in L, C, and R Applied voltage: & current: time domain Phase angle factor ej. F rotates E CCW from the current phasor Passive circuit elements: Resistor: Inductor: Capacitor: VR& IRm in phase VL leads ILm by p/2 VC lags ICm by p/2 Rotations of voltage drop phasors relative to current phasor: e 0 =1 e+jp/2 = +j e-jp/2 = -j Voltage drop phasors relative to currents: time domain Frequency domain (factor out time dependence) Define: Complex impedance z = E(t)/i(t) and |z| = Vmax/Imax Impedances of simple circuit elements (complex) are: Magnitudes of Impedances |z| = [zz*]1/2 (real) Copyright R. Janow – Fall 2015

Complex Impedance z Applied voltage: & current: time domain Definition: complex impedance z (or simply impedance) is the ratio of the (complex) voltage phasor to the (complex) current phasor (in time or frequency domain). Definition: Phase angle F measures rotation of the applied voltage referenced to the current in the branch. It is also the angle between z and the real axis. The rotation operator is ej. F. Sketch shows positive Im{z}. F is positive, implying that Em leads Im. Im Z 1/z occurs when analyzing parallel branches: Im(z) Em Im F Re(z) Re Copyright R. Janow – Fall 2015

Impedances of Series or Parallel Collections of Circuit Elements Impedances of individual passive circuit elements: The kth sub-circuit (arbitrary complexity) consists of R, L, and/or C basic elements: zk Assertion: Follow series or parallel resistor addition rules to compute equivalent impedances (complex) Series branch formula: zk z 2 z 1 Parallel sub-circuit formula: z 1 z 2 zk Copyright R. Janow – Fall 2015

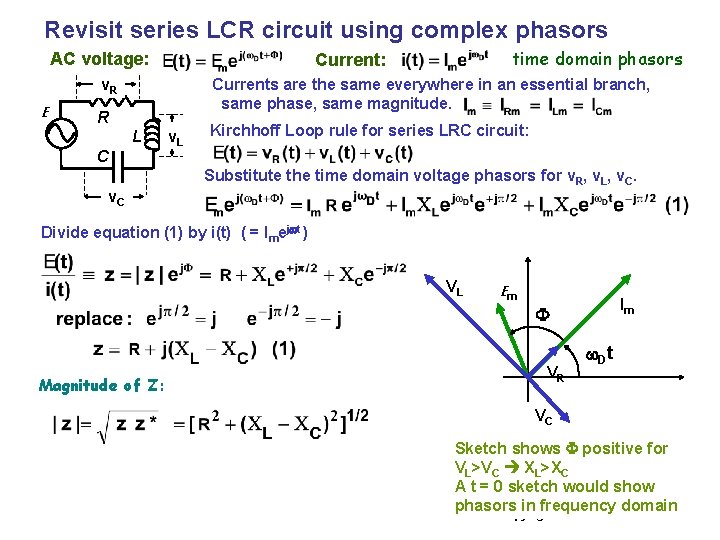
Revisit series LCR circuit using complex phasors AC voltage: Currents are the same everywhere in an essential branch, same phase, same magnitude. v. R E time domain phasors Current: R L v. L Kirchhoff Loop rule for series LRC circuit: C Substitute the time domain voltage phasors for v. R, v. L, v. C Divide equation (1) by i(t) ( = Imejwt ) VL Em Im F Magnitude of Z: VR w. D t VC Sketch shows F positive for VL>VC XL>XC A t = 0 sketch would show phasors in frequency domain Copyright R. Janow – Fall 2015

Revisit the series LCR circuit, Continuation Impedance z (Equation 1) can also be found by summing the impedances of the 3 basic circuit elements in series LCR circuit (invoke Series Formula*) Im Z z is not a phasor, as it is time independent. Previous “phasor diagrams” showed z rotating with Em. Phase angle F for the circuit: Power factor: XL-XC F R Re Sketch shows F >0 for XL > XC VL > VC. F is positive when Im{z} is positive * The equivalent (complex) impedance for circuit elements in series (arbitrarily many) is the sum of the individual (complex) impedances. Resonance: As before, z is real for XL= XC (w 2 = 1/LC). |z| is minimized. Current amplitude Im is maximized at resonance Phase angle in terms of admittance 1/z: Copyright R. Janow – Fall 2015

Parallel LCR circuit using complex phasors All steady state voltages and currents oscillate at driving frequency w. D AC voltage: Instantaneous Current: i E a i. R i. L v. R i. C v. L R L v. C C b Kirchhoff Loop Rule (time domain): • 2 essential nodes “a” & “b” • 4 essential branches, • Not all independent Instantaneous voltages across parallel branches have the same magnitude and Use voltage as reference phase: instead of current Common voltage phase, all branches: Common voltage peak, all branches: Kichhoff Current Rule (node a or b): Current Amplitudes in each parallel branch (reference now to voltage drop): Copyright R. Janow – Fall 2015

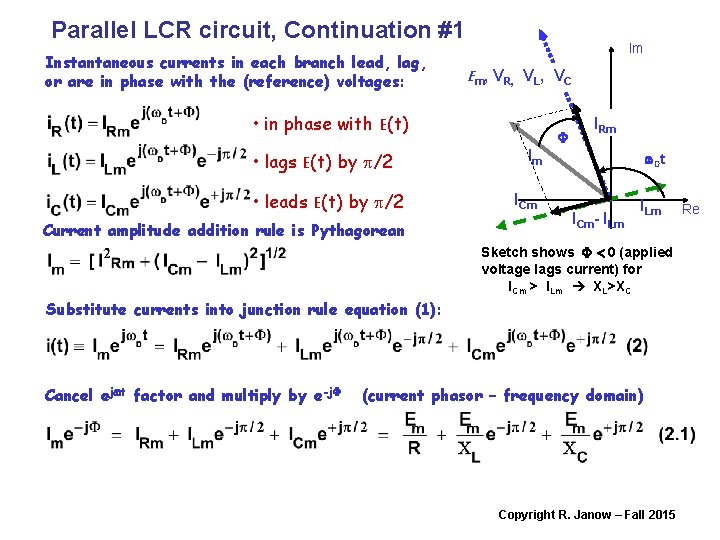
Parallel LCR circuit, Continuation #1 Instantaneous currents in each branch lead, lag, or are in phase with the (reference) voltages: Im Em, VR, VL, VC • in phase with E(t) • lags E(t) by p/2 • leads E(t) by p/2 Current amplitude addition rule is Pythagorean F IRm Im ICm w. Dt ICm- ILm Sketch shows F < 0 (applied voltage lags current) for ICm > ILm XL>XC Substitute currents into junction rule equation (1): Cancel ejwt factor and multiply by e-j. F (current phasor – frequency domain) Copyright R. Janow – Fall 2015 Re

Parallel LCR circuit, continuation #2 Recall, impedance “admittance” Note that: Substitute, then divide (Eq. 2. 1) above by Em Admittance 1/z in Equation 3 is also the sum of the reciprocal impedances of the 3 basic circuit elements in parallel LCR circuit (invoke Parallel Formula) Find |1/z|: multiply 1/z by complex conjugate (1/z)* and take square root: Represent z in terms of 1/z: Copyright R. Janow – Fall 2015

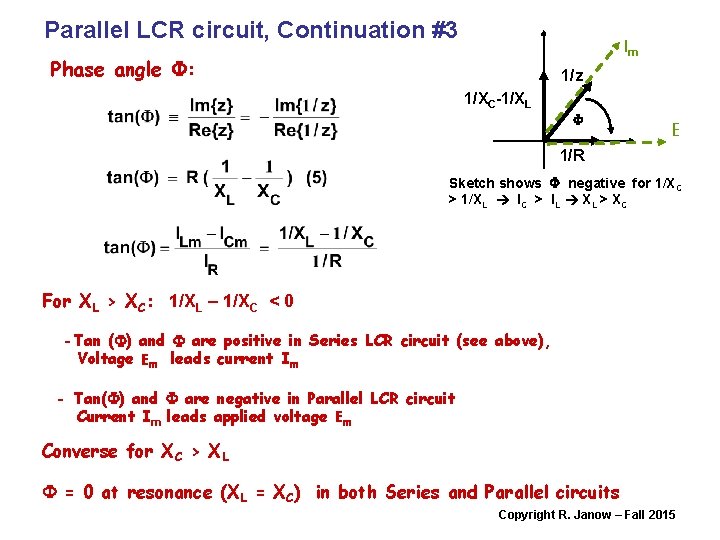
Parallel LCR circuit, Continuation #3 Im Phase angle F: 1/z 1/XC-1/XL F E 1/R Sketch shows F negative for 1/XC > 1/XL IC > IL XL > XC For XL > XC: 1/XL – 1/XC < 0 -Tan (F) and F are positive in Series LCR circuit (see above), Voltage Em leads current Im - Tan(F) and F are negative in Parallel LCR circuit Current Im leads applied voltage Em Converse for XC > XL F = 0 at resonance (XL = XC) in both Series and Parallel circuits Copyright R. Janow – Fall 2015

Parallel LCR circuit, Continuation #4 Resonance: Minimizes as function of frequency Minimum of 1/|z| when XL = XC, i. e. when w 2 = 1/LC Same resonant frequency as series LCR, but current is minimized instead of maximized at resonance At resonance, the current amplitudes ILm and ICm in the L & C branches are equal, but are 180 o apart in phase. These cancel at all times at nodes a and b of the circuit. Copyright R. Janow – Fall 2015

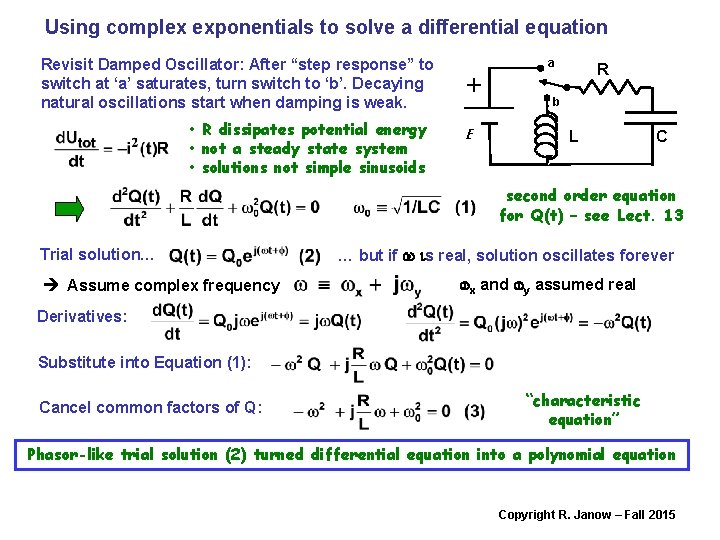
Using complex exponentials to solve a differential equation Revisit Damped Oscillator: After “step response” to switch at ‘a’ saturates, turn switch to ‘b’. Decaying natural oscillations start when damping is weak. • R dissipates potential energy • not a steady state system • solutions not simple sinusoids a + E R b L C second order equation for Q(t) – see Lect. 13 Trial solution… Assume complex frequency … but if w is real, solution oscillates forever wx and wy assumed real Derivatives: Substitute into Equation (1): Cancel common factors of Q: “characteristic equation” Phasor-like trial solution (2) turned differential equation into a polynomial equation Copyright R. Janow – Fall 2015

Using complex exponentials to solve a differential equation, #2 Expand: Equation (3) becomes 2 separate equations for real and imaginary terms Im{Eq 3} Re{Eq 3} Substitute wy: Shifted natural frequency wx is real for imaginary for underdamping overdamping For real wx (underdamping): damping oscillation For critical damping, wx = 0: No oscillations, decay only: Copyright R. Janow – Fall 2015

Using complex exponentials to solve a differential equation, #3 wx becomes imaginary. Equations 4. 1 & 4. 2 invalid For overdamping: Return to Eq. 3. 0. Assume frequency is pure imaginary ( no oscillation) Eq. 3. 0 becomes: quadratic, real coefficients Solution: two roots both pure imaginary Both roots lead to decay w/o oscillation + root: w+ implies damping faster than e-Rt/2 L - root: w- implies damping slower than e-Rt/2 L but not growth Most general solution: linear combination of Q+ and Q-, each of form of Eq. 2. 0 Recall definition, hyperbolic cosine: Correctly reduces to critically damped Eq. 8. 0 Copyright R. Janow – Fall 2015

Copyright R. Janow – Fall 2015