Physics 121 Electricity and Magnetism Lecture 14 AC

Physics 121 - Electricity and Magnetism Lecture 14 - AC Circuits, Resonance Y&F Chapter 31, Sec. 1 - 8 • • AC Circuits, Phasors, Forced Oscillations Phase Relations for Current and Voltage in Simple Resistive, Capacitive, Inductive Circuits Phasor Diagrams for Voltage and Current The Series RLC Circuit. Amplitude and Phase Relations Impedance and Phasors for Impedance Resonance Power in AC Circuits, Power Factor Transformers Copyright R. Janow –Fall 2017

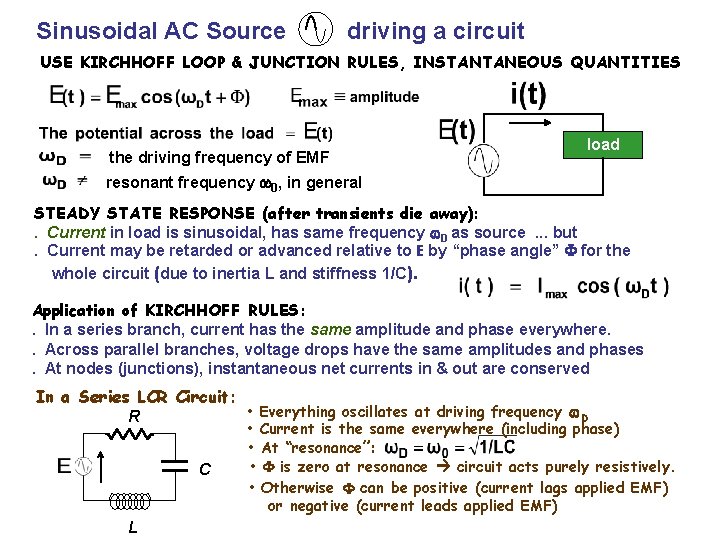
Sinusoidal AC Source driving a circuit USE KIRCHHOFF LOOP & JUNCTION RULES, INSTANTANEOUS QUANTITIES the driving frequency of EMF load resonant frequency w 0, in general STEADY STATE RESPONSE (after transients die away): . Current in load is sinusoidal, has same frequency w. D as source. . . but. Current may be retarded or advanced relative to E by “phase angle” F for the whole circuit (due to inertia L and stiffness 1/C). Application of KIRCHHOFF RULES: . In a series branch, current has the same amplitude and phase everywhere. . Across parallel branches, voltage drops have the same amplitudes and phases. At nodes (junctions), instantaneous net currents in & out are conserved In a Series LCR Circuit: R C L • Everything oscillates at driving frequency w. D • Current is the same everywhere (including phase) • At “resonance”: • F is zero at resonance circuit acts purely resistively. • Otherwise F can be positive (current lags applied EMF) Copyright R. Janow –Fall 2017 or negative (current leads applied EMF)

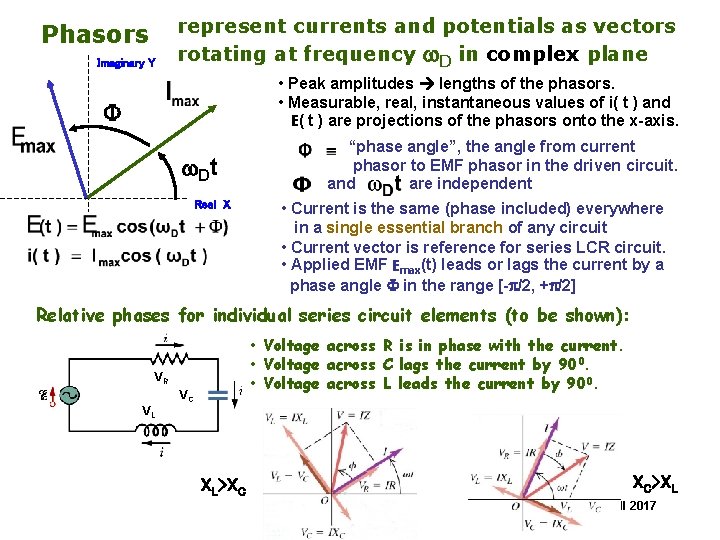
represent currents and potentials as vectors rotating at frequency w. D in complex plane Phasors Imaginary Y • Peak amplitudes lengths of the phasors. • Measurable, real, instantaneous values of i( t ) and E( t ) are projections of the phasors onto the x-axis. F w. D t Real X “phase angle”, the angle from current phasor to EMF phasor in the driven circuit. and are independent • Current is the same (phase included) everywhere in a single essential branch of any circuit • Current vector is reference for series LCR circuit. • Applied EMF Emax(t) leads or lags the current by a phase angle F in the range [-p/2, +p/2] Relative phases for individual series circuit elements (to be shown): • Voltage across R is in phase with the current. • Voltage across C lags the current by 900. • Voltage across L leads the current by 900. VR VC VL XL>XC XC>XL Copyright R. Janow –Fall 2017

The meaningful types of quantities in AC circuits can be instantaneous, peak, or average (RMS) Instantaneous voltages and currents refer to a specific time: • oscillatory, depend on time through argument “wt” • possibly advanced or retarded relative to each other by phase angle • represented by x-component of rotating “phasors” – see slides below Peak voltage and current amplitudes are just the coefficients out front • represented by lengths of rotating phasors Simplistic time averaging of periodic quantities gives zero (and useless) results). • example: integrate over a whole number of periods – one t is enough (wt=2 p) Integrand is odd over a full cycle Copyright R. Janow –Fall 2017 So how should “average” be defined?

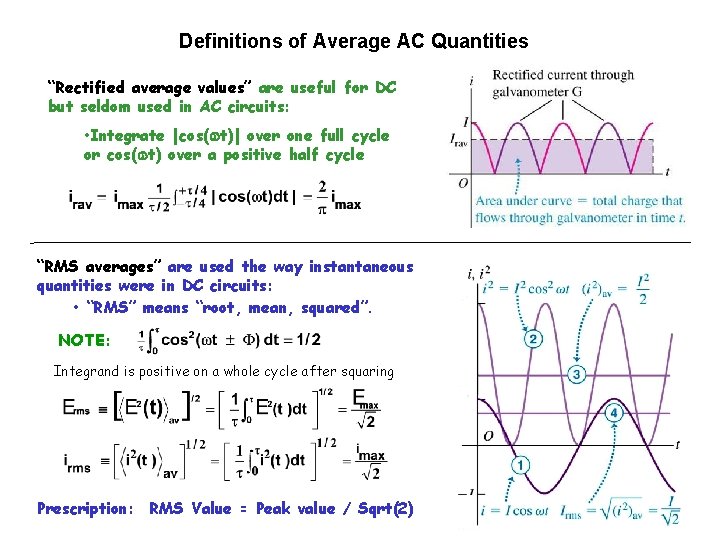
Definitions of Average AC Quantities “Rectified average values” are useful for DC but seldom used in AC circuits: • Integrate |cos(wt)| over one full cycle or cos(wt) over a positive half cycle “RMS averages” are used the way instantaneous quantities were in DC circuits: • “RMS” means “root, mean, squared”. NOTE: Integrand is positive on a whole cycle after squaring Prescription: RMS Value = Peak value / Sqrt(2) Copyright R. Janow –Fall 2017

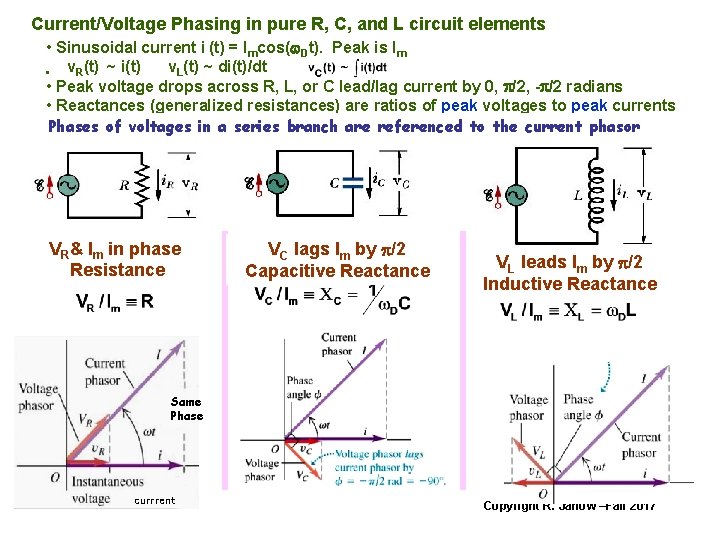
Current/Voltage Phasing in pure R, C, and L circuit elements • Sinusoidal current i (t) = Imcos(w. Dt). Peak is Im v. R(t) ~ i(t) v. L(t) ~ di(t)/dt • • Peak voltage drops across R, L, or C lead/lag current by 0, p/2, -p/2 radians • Reactances (generalized resistances) are ratios of peak voltages to peak currents Phases of voltages in a series branch are referenced to the current phasor VR& Im in phase Resistance VC lags Im by p/2 Capacitive Reactance VL leads Im by p/2 Inductive Reactance Same Phase currrent Copyright R. Janow –Fall 2017

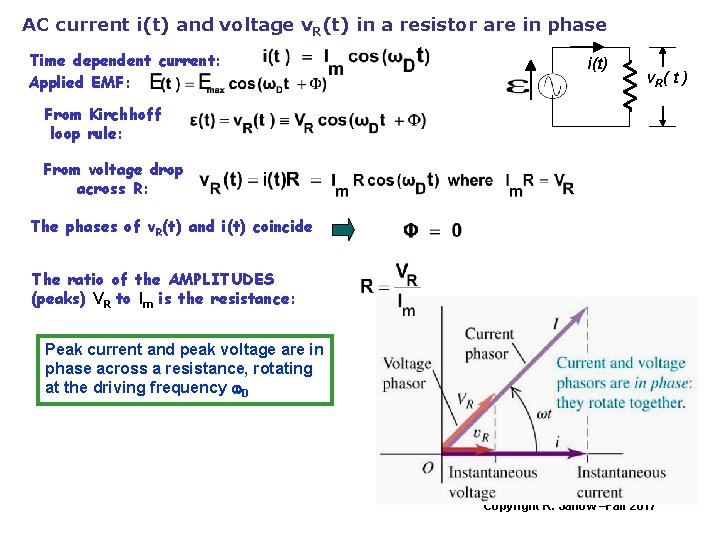
AC current i(t) and voltage v. R(t) in a resistor are in phase Time dependent current: Applied EMF: i(t) v R( t ) From Kirchhoff loop rule: From voltage drop across R: The phases of v. R(t) and i(t) coincide The ratio of the AMPLITUDES (peaks) VR to Im is the resistance: Peak current and peak voltage are in phase across a resistance, rotating at the driving frequency w. D Copyright R. Janow –Fall 2017

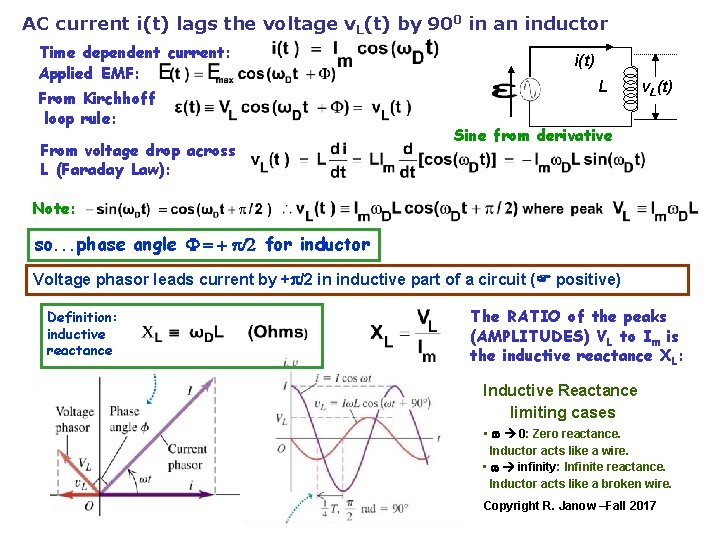
AC current i(t) lags the voltage v. L(t) by 900 in an inductor Time dependent current: Applied EMF: From Kirchhoff loop rule: From voltage drop across L (Faraday Law): i(t) L v. L(t) Sine from derivative Note: so. . . phase angle F = + p/2 for inductor Voltage phasor leads current by +p/2 in inductive part of a circuit (F positive) Definition: inductive reactance The RATIO of the peaks (AMPLITUDES) VL to Im is the inductive reactance XL: Inductive Reactance limiting cases • w 0: Zero reactance. Inductor acts like a wire. • w infinity: Infinite reactance. Inductor acts like a broken wire. Copyright R. Janow –Fall 2017

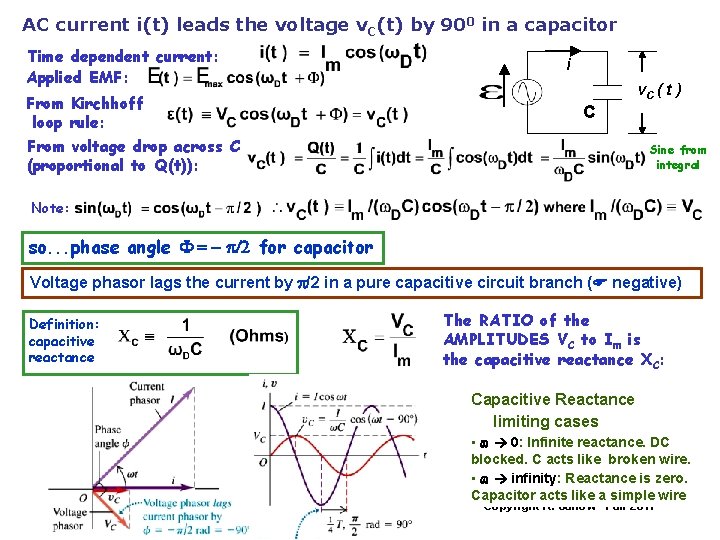
AC current i(t) leads the voltage v. C(t) by 900 in a capacitor Time dependent current: Applied EMF: From Kirchhoff loop rule: i v. C ( t ) C From voltage drop across C (proportional to Q(t)): Sine from integral Note: so. . . phase angle F = - p/2 for capacitor Voltage phasor lags the current by p/2 in a pure capacitive circuit branch (F negative) Definition: capacitive reactance The RATIO of the AMPLITUDES VC to Im is the capacitive reactance XC: Capacitive Reactance limiting cases • w 0: Infinite reactance. DC blocked. C acts like broken wire. • w infinity: Reactance is zero. Capacitor acts like a simple wire Copyright R. Janow –Fall 2017

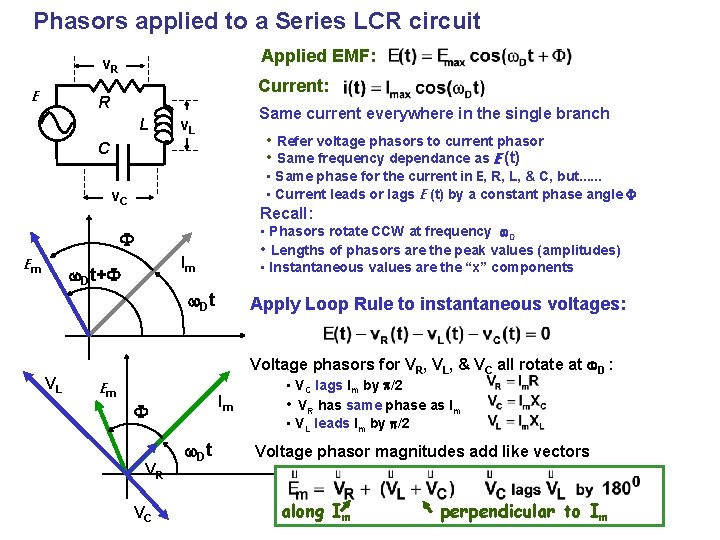
Phasors applied to a Series LCR circuit Applied EMF: v. R E Current: R L Same current everywhere in the single branch v. L • Refer voltage phasors to current phasor • Same frequency dependance as E (t) C • Same phase for the current in E, R, L, & C, but. . . • Current leads or lags E (t) by a constant phase angle F v. C Recall: • Phasors rotate CCW at frequency w. D • Lengths of phasors are the peak values (amplitudes) • Instantaneous values are the “x” components F Em Im w. Dt+F w. D t VL Apply Loop Rule to instantaneous voltages: Voltage phasors for VR, VL, & VC all rotate at w. D : Em Im F VR VC w. D t • VC lags Im by p/2 • VR has same phase as Im • VL leads Im by p/2 Voltage phasor magnitudes add like vectors along Im Copyright R. Janow –Fall 2017 perpendicular to Im

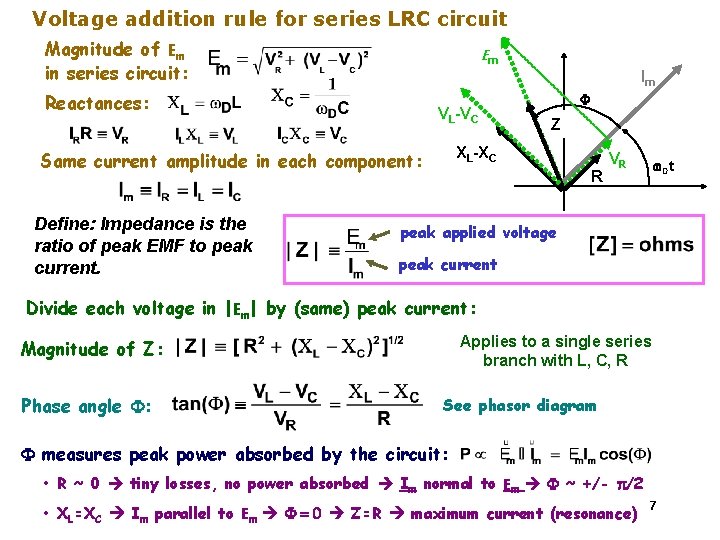
Voltage addition rule for series LRC circuit Magnitude of Em in series circuit: Em Im Reactances: Z XL-XC Same current amplitude in each component: Define: Impedance is the ratio of peak EMF to peak current. F VL-VC R VR w. Dt peak applied voltage peak current Divide each voltage in |Em| by (same) peak current: Applies to a single series branch with L, C, R Magnitude of Z: Phase angle F: See phasor diagram F measures peak power absorbed by the circuit: • R ~ 0 tiny losses, no power absorbed Im normal to Em F ~ +/- p/2 Copyright R. Janow –Fall 2017 • XL=XC Im parallel to Em F = 0 Z=R maximum current (resonance)

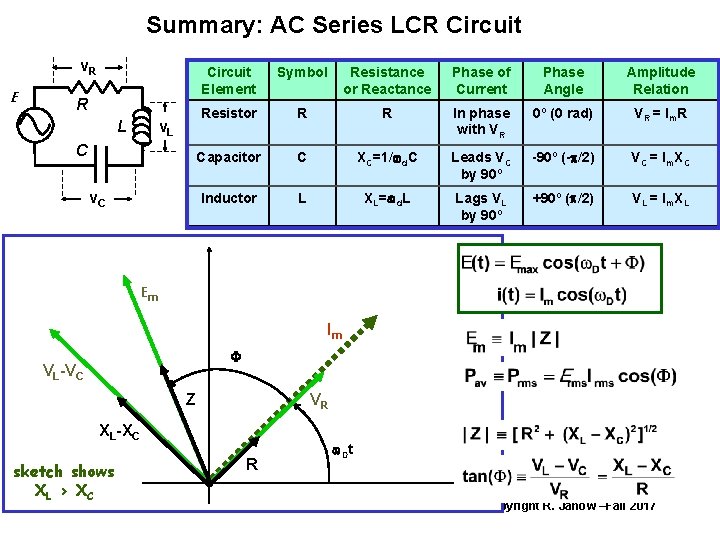
Summary: AC Series LCR Circuit v. R E R L v. L C v. C Circuit Element Symbol Resistance or Reactance Phase of Current Phase Angle Amplitude Relation Resistor R R In phase with VR 0º (0 rad) VR = Im R Capacitor C XC=1/wd. C Leads VC by 90º -90º (-p/2) VC = Im XC Inductor L XL=wd. L Lags VL by 90º +90º (p/2) VL = Im XL Em Im F VL-VC Z VR XL-XC sketch shows XL > X C R w. Dt Copyright R. Janow –Fall 2017

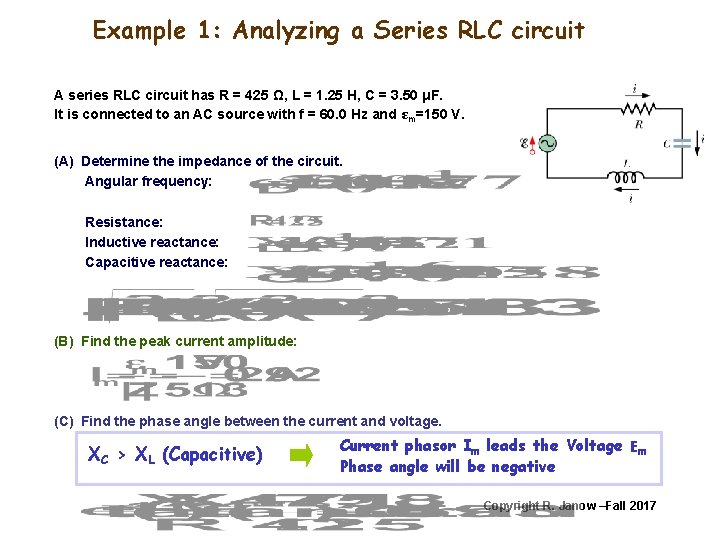
Example 1: Analyzing a series RLC circuit A series RLC circuit has R = 425 Ω, L = 1. 25 H, C = 3. 50 μF. It is connected to an AC source with f = 60. 0 Hz and εm= 150 V. (A) (B) (C) (D) (E) Determine the impedance of the circuit. Find the amplitude of the current (peak value). Find the phase angle between the current and voltage. Find the instantaneous current across the RLC circuit. Find the peak and instantaneous voltages across each circuit element. Copyright R. Janow –Fall 2017

Example 1: Analyzing a Series RLC circuit A series RLC circuit has R = 425 Ω, L = 1. 25 H, C = 3. 50 μF. It is connected to an AC source with f = 60. 0 Hz and εm=150 V. (A) Determine the impedance of the circuit. Angular frequency: Resistance: Inductive reactance: Capacitive reactance: (B) Find the peak current amplitude: (C) Find the phase angle between the current and voltage. XC > XL (Capacitive) Current phasor Im leads the Voltage Em Phase angle will be negative Copyright R. Janow –Fall 2017

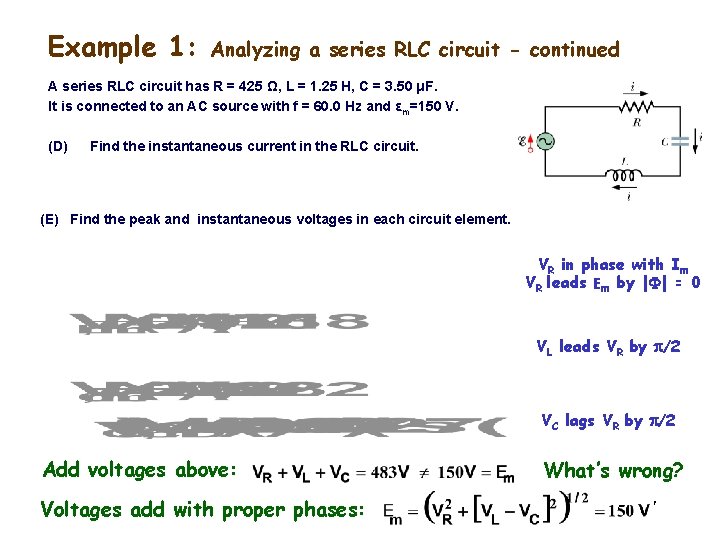
Example 1: Analyzing a series RLC circuit - continued A series RLC circuit has R = 425 Ω, L = 1. 25 H, C = 3. 50 μF. It is connected to an AC source with f = 60. 0 Hz and εm=150 V. (D) Find the instantaneous current in the RLC circuit. (E) Find the peak and instantaneous voltages in each circuit element. VR in phase with Im VR leads Em by |F| = 0 VL leads VR by p/2 VC lags VR by p/2 Add voltages above: Voltages add with proper phases: What’s wrong? Copyright R. Janow –Fall 2017

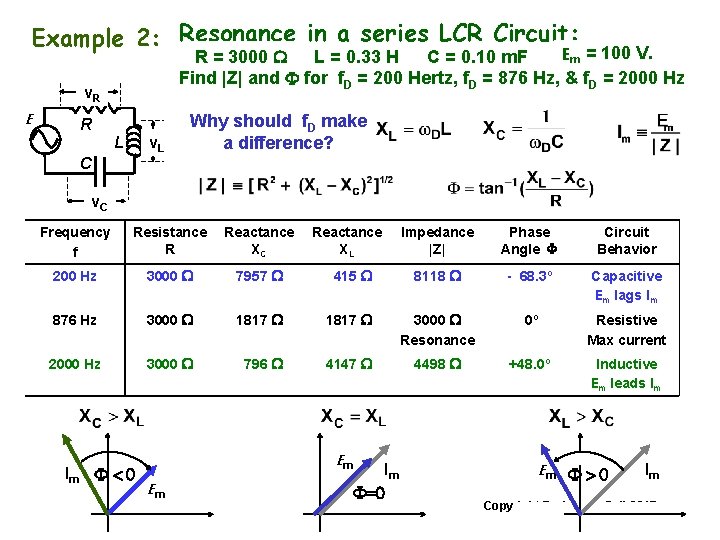
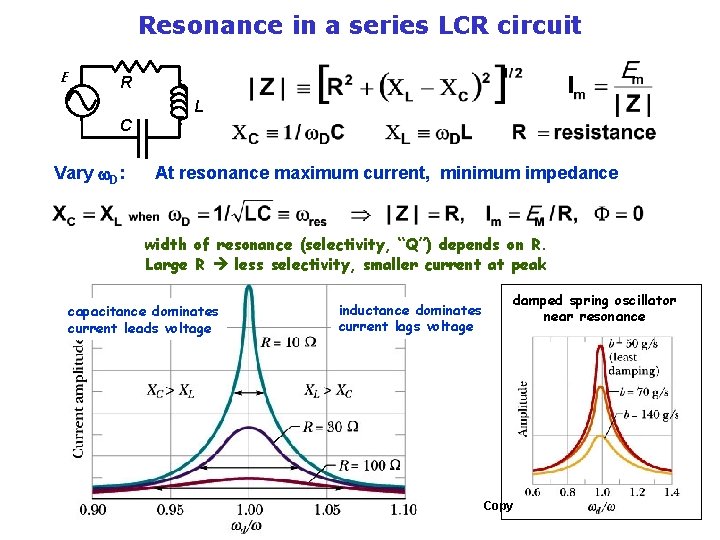
Example 2: Resonance in a series LCR Circuit: Em = 100 V. R = 3000 W L = 0. 33 H C = 0. 10 m. F Find |Z| and F for f. D = 200 Hertz, f. D = 876 Hz, & f. D = 2000 Hz v. R E R L v. L C Why should f. D make a difference? v. C Frequency f Resistance R Reactance XC 200 Hz 3000 W 7957 W 876 Hz 3000 W 2000 Hz 3000 W Im F < 0 Reactance XL Impedance |Z| Phase Angle F Circuit Behavior 415 W 8118 W - 68. 3º Capacitive Em lags Im 1817 W 3000 W Resonance 0º Resistive Max current 796 W 4147 W 4498 W +48. 0º Inductive Em leads Im Em Em Im F=0 Em F > 0 Im Copyright R. Janow –Fall 2017

Resonance in a series LCR circuit E R L C Vary w. D: At resonance maximum current, minimum impedance width of resonance (selectivity, “Q”) depends on R. Large R less selectivity, smaller current at peak capacitance dominates current leads voltage inductance dominates current lags voltage damped spring oscillator near resonance Copyright R. Janow –Fall 2017

Power in AC Circuits • Resistors always dissipate power, but the instantaneous rate varies as i 2(t)R • No power is lost in pure capacitors and pure inductors in an AC circuit – Capacitor stores energy during two 1/4 cycle segments. During two other segments energy is returned to the circuit – Inductor stores energy when it produces opposition to current growth during two ¼ cycle segments (the source does work). When the current in the circuit begins to decrease, the energy is returned to the circuit Copyright R. Janow –Fall 2017

AC Power Dissipation in a Resistor Instantaneous power • Power is dissipated in R, not in L or C • cos 2(x) is always positive, so Pinst is always positive. But, it is not constant. • Power pattern repeats every p radians (t/2) The RMS power is an AC equivalent to DC power Integrate Pinst in resistor over t: Integral = 1/2 RMS means “Root Mean Square” • Square a quantity (positive) • Average over a whole cycle • Compute square root. COMPUTING RMS QUANTITIES: • For any RMS quantity divide peak value such as Im or Em by sqrt(2) For any R, L, or C R. Janow –Fall 2017 Household power example: 120 volts RMS Copyright 170 volts peak

Power factor for an AC LCR Circuit The PHASE ANGLE F determines the average RMS power actually absorbed due to the RMS current and applied voltage in the circuit. Erms Irms F Claim (proven below): |Z| XL-XC R w. D t Proof: Start with instantaneous power (not very useful): Average it over one full period t: Change variables: Use trig identity: Copyright R. Janow –Fall 2017

Power factor for AC Circuits - continued Odd integrand Even integrand Recall: RMS values = Peak values divided by sqrt(2) Also note: Alternate form: If R=0 (pure LC circuit) F +/- p/2 and Pav = Prms = 0 Copyright R. Janow –Fall 2017

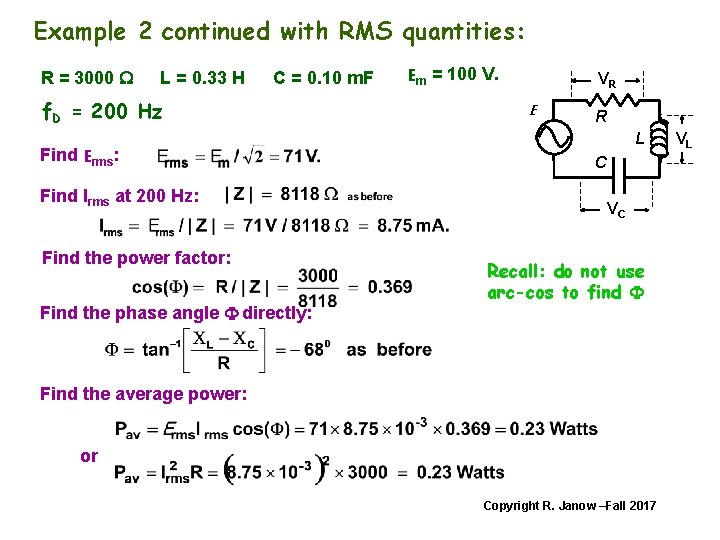
Example 2 continued with RMS quantities: R = 3000 W L = 0. 33 H C = 0. 10 m. F f. D = 200 Hz Find Erms: Find Irms at 200 Hz: Find the power factor: Find the phase angle F directly: Em = 100 V. VR E R L C VC Recall: do not use arc-cos to find F Find the average power: or Copyright R. Janow –Fall 2017 VL

Example 3 – Use RMS values in. Series LCR circuit analysis A 240 V (RMS), 60 Hz voltage source is applied to a series LCR circuit consisting of a 50 ohm resistor, a 0. 5 H inductor and a 20 m. F capacitor. Find the capacitive reactance of the circuit: Find the inductive reactance of the circuit: The impedance of the circuit is: The phase angle for the circuit is: F is positive since XL>XC (inductive) The RMS current in the circuit is: The average power consumed in this circuit is: If the inductance could be changed to maximize the current through the circuit, what would the new inductance L’ be? How much RMS current would flow in that case? Copyright R. Janow –Fall 2017

Transformers Devices used to change AC voltages. They have: • Primary winding • Secondary winding • Power ratings power transformer iron core circuit symbol Copyright R. Janow –Fall 2017

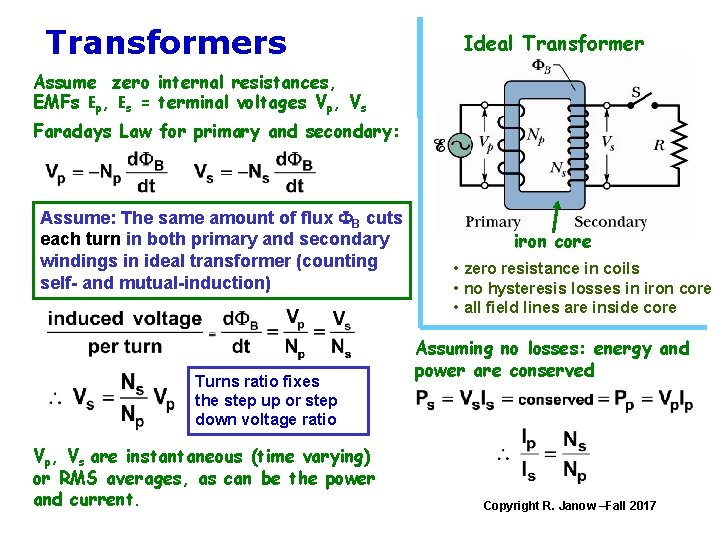
Transformers Ideal Transformer Assume zero internal resistances, EMFs Ep, Es = terminal voltages Vp, Vs Faradays Law for primary and secondary: Assume: The same amount of flux FB cuts each turn in both primary and secondary windings in ideal transformer (counting self- and mutual-induction) Turns ratio fixes the step up or step down voltage ratio Vp, Vs are instantaneous (time varying) or RMS averages, as can be the power and current. iron core • zero resistance in coils • no hysteresis losses in iron core • all field lines are inside core Assuming no losses: energy and power are conserved Copyright R. Janow –Fall 2017

Example: A dimmer for lights using a variable inductance f =60 Hz w = 377 rad/sec Light bulb R=50 W Erms=30 V L Without Inductor: a) What value of the inductance would dim the lights to 5 Watts? Recall: b) What would be the change in the RMS current? Without inductor: P 0, rms = 18 W. With inductor: Prms = 5 W. Copyright R. Janow –Fall 2017