Perfect Noninteractive ZeroKnowledge for NP Jens Groth Rafail

Perfect Non-interactive Zero-Knowledge for NP Jens Groth Rafail Ostrovsky Amit Sahai University of California Los Angeles

Motivation OK, I will make a I’m azero-knowledge woman. Prove it! proof Circuit C = ”I’m a woman” Proof π

Completeness Common reference string Circuit C Witness w so C(w)=1 Proof π K(1 k) Accept Prover Verifier Perfect completeness: Pr[Accept] = 1

Soundness Common reference string K(1 k) Unsatisfiable C Proof π Adversary Verifier Perfect soundness: Pr[Reject] = 1 Reject

S 1(1 k ) Zero-knowledge sk S 2(crs, sk, C) Simulator ”Common reference string” Circuit C Witness w Proof π Adversary Computational zero-knowledge: Pr[A 1|Simulated proofs (S 1, S 2)] ≈ Pr[A 1|Real proofs (K, P)] 0/1

State of affairs Computational NIZK proofs known but not practical Kilian-Petrank: O(|C|k 2)-bit common reference string O(|C|k 2)-bit proofs n Statistical/perfect NIZK arguments not known n No non-interactive UC ZK arguments secure against adaptive adversaries known n

Our contributions NIZK proof for Circuit SAT - Perfect completeness, perfect soundness, perfect proof of knowledge, computational zero-knowledge - O(k)-bit common reference string - O(|C|k)-bit proofs n Perfect NIZK argument for Circuit SAT - Perfect completeness, computational co. NP soundness, perfect zero-knowledge n UC NIZK argument for Circuit SAT with perfect zero-knowledge secure against adaptive adversaries n

Bilinear group of order n G, G 1 cyclic groups of order n = pq g generator for G bilinear map e: G G G 1 e(ua, vb) = e(u, v)ab e(g, g) generates G 1 Decision subgroup problem ord(h) = q or ord(h) = n ?

Boneh-Goh-Nissim cryptosystem Key generation pk = (n, G, G 1, e, g, h) ord(h) = q ord(g) = n, sk = (pk, p, q) Encryption of m E(m; r) = gmhr |m|=O(log k) where r Zn Decryption (gmhr)q = (gq)m find m by polynomial time

Homomorphic properties Additively homomorphic gm 1 hr 1 gm 2 hr 2 = gm 1+m 2 hr 1+r 2 Multiplication-mapping e(gm 1 hr 1, gm 2 hr 2) = e(g, g)m 1 m 2 e(h, gm 1 r 2+m 2 r 1 hr 1 r 2)

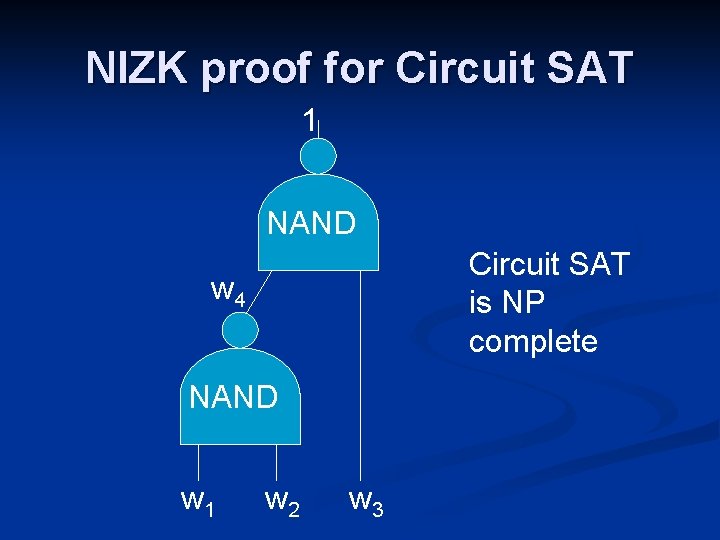
NIZK proof for Circuit SAT 1 NAND Circuit SAT is NP complete w 4 NAND w 1 w 2 w 3

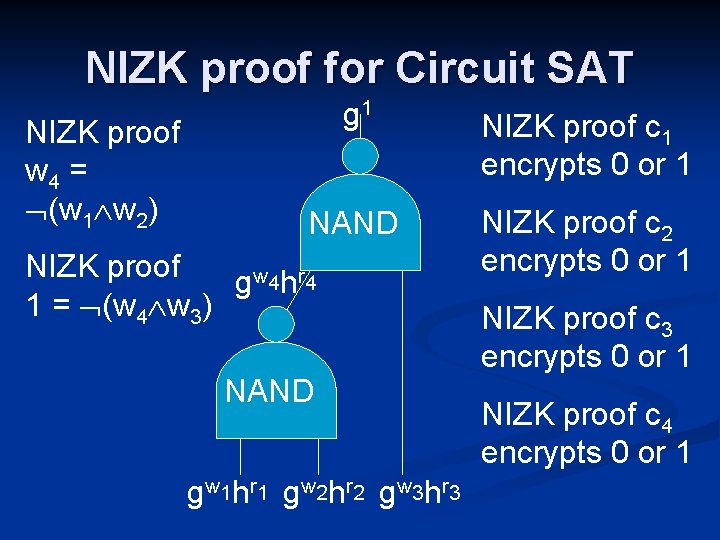
NIZK proof for Circuit SAT NIZK proof w 4 = (w 1 w 2) g 1 NIZK proof c 1 encrypts 0 or 1 NAND NIZK proof c 2 encrypts 0 or 1 NIZK proof g w 4 h r 4 1 = (w 4 w 3) NAND g w 1 h r 1 g w 2 h r 2 g w 3 h r 3 NIZK proof c 3 encrypts 0 or 1 NIZK proof c 4 encrypts 0 or 1

NIZK proof for encryption of 0 or 1 Wish to prove c encrypts 0 or 1 Write c = gmhr (m uniquely determined mod p) e(c, g-1 c) = e(gmhr, gm-1 hr) = e(g, g)m(m-1) e(hr, g 2 m-1 hr) has order q if and only if m = 0 mod p or m = 1 mod p We wish to prove e(c, g-1 c) has order q

NIZK proof for encryption of 0 or 1 Prover chooses s Zn* e(c, g-1 c) = e(gmhr, gm-1 hr) = e(hr, g 2 m-1 hr) = e(hs, (g 2 m-1 hr)r/s) Reveal π = (π1, π2, π3) π1 = hs π2 = (g 2 m-1 hr)r/s π3 = gs Verifier checks e(π1, g) = e(h, π3) and e(c, g-1 c) = e(π1, π 2)

NIZK proof for encryption of 0 or 1 Perfect soundness h has order q e(h, π3) has order q e(π1, g) = e(h, π3) e(π1, g) has order q π1 has order q e(π1, π2) has order q e(c, g-1 c) = e(π1, π2) e(c, g-1 c) has order q m = 0 mod p or m = 1 mod p Computational zero-knowledge

NIZK proof for NAND-gate Given c 0, c 1, c 2 ciphertexts containing bits b 0, b 1, b 2 wish to prove b 2 = (b 0 b 1) if and only if b 0 + b 1 + 2 b 2 - 2 {0, 1} Make NIZK proof for c 0 c 1 c 22 g-2 encrypting 0 or 1

NIZK proof for Circuit SAT Encrypt all wires wi as ci = gwihri n For each i make NIZK that ci contains 0 or 1 n For each NAND-gate make NIZK proof that c 0 c 1 c 22 g-2 contains 0 or 1 n Perfect completeness Perfect soundness Computational zero-knowledge Perfect knowledge extraction – decrypt ciphertexts

Perfect NIZK Common reference string (g, h) Choose g, h so ord(g) = ord(h) = n Perfect completeness Perfect zero-knowledge Ciphertexts ci are perfectly hiding commitments NIZK argument for 0/1 plaintexts perfect ZK

Adaptive co. NP soundness Common reference string C, wco Proof π K(1 k) Reject wco witness for C unsatisfiable Computational co. NP soundness: Pr[Reject] ≈ 1

FNIZK (prove, C, w) (proof, π) (verify, C, π) (verification, 0/1) If C(w)=1 give C to S and get π store (C, π) If (C, π) not stored give (C, π) to S and get w if C(w)=1 store (C, π) Return 1 if (C, π) stored

UC NIZK There exists non-interactive protocol UC NIZK such that 1. 2. UC NIZK securely realizes FNIZK against adaptive adversaries in the common reference string model UC NIZK is perfect zero-knowledge

Conclusion New technique for NIZK proofs 1. Very efficient NIZK proofs with perfect soundness 2. First construction of perfect zeroknowledge NIZK argument with co. NP soundness 3. First construction of UC NIZK argument secure against adaptive adversaries