Paradox Lost The Evils of Coins and Dice

• What’s Best? Arthur T. Benjamin and Matthew T. Fluet, American Mathematical Monthly

Definition: The qth percentile is the number k for which P (X<k)<q/100 and P(X≤k)>q/100.

Theorem (Benjamin, Fluet) Flipping a coin with probability of heads p, the configuration of

• The Best Way to Knock ’m Down, Art Benjamin and Matthew Fluet,

• The River Crossing Game, David Goering and Dan Canada, Mathematics Magazine 80:

2 3 4 5 6 7 8 9 10 11 12 Probability Expected #

Relative probability (and probability) wins race is 0. 293. 2 3 4 5 6

Relative probability down to 0. 278 from 0. 293. 2 3 4 5 6

Relative probability increases to 0. 517 by the time 28 ships are on 5

Relative probability is small and decreases at first, but ultimately increases to 1. 2

• Waiting Times for Patterns and a Method of Gambling Teams, Vladimir Pozdnyakov

HTHH vs HHTT • Which happens fastest on average? • Which is more likely

Expected Number of Flips to See the Sequence 30 HHHH 20 HTHT 18 HTHH

• The expected duration for sequences with more than two outcomes and not

• The expected time to hit a sequence S given a head start

Racing sequences S 1, …, Sn • Probabilities of winning p 1, …, pn

Probabilities of Winning Races HTHH 4/7 HHTT 3/7 # Flips 10. 28… Yet the

Probabilities of Winning Races HTHH 4/7 HHTT 9/16 HHTT 3/7 THTH 7/16 # Flips

Probabilities of Winning Races HTHH 4/7 HHTT 9/16 HTHH 5/14 HHTT 3/7 THTH 7/16

Slides: 31

Download presentation

Paradox Lost: The Evils of Coins and Dice George Gilbert October 6, 2010

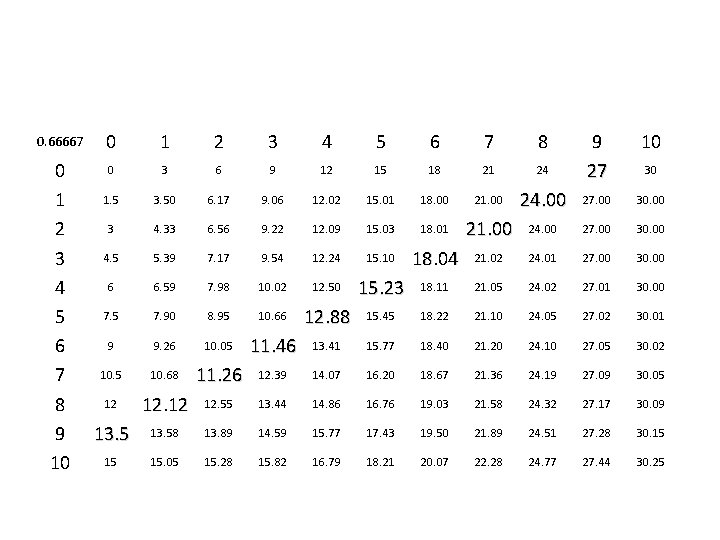
0. 66667 0 1 2 3 4 5 6 7 8 10 24 9 27 0 1 2 3 4 5 6 7 8 9 10 0 3 6 9 12 15 18 21 1. 5 3. 50 6. 17 9. 06 12. 02 15. 01 18. 00 21. 00 24. 00 27. 00 30. 00 3 4. 33 6. 56 9. 22 12. 09 15. 03 18. 01 21. 00 24. 00 27. 00 30. 00 4. 5 5. 39 7. 17 9. 54 12. 24 15. 10 18. 04 21. 02 24. 01 27. 00 30. 00 6 6. 59 7. 98 10. 02 12. 50 15. 23 18. 11 21. 05 24. 02 27. 01 30. 00 7. 5 7. 90 8. 95 10. 66 12. 88 15. 45 18. 22 21. 10 24. 05 27. 02 30. 01 9 9. 26 10. 05 11. 46 13. 41 15. 77 18. 40 21. 20 24. 10 27. 05 30. 02 10. 5 10. 68 11. 26 12. 39 14. 07 16. 20 18. 67 21. 36 24. 19 27. 09 30. 05 12 12. 55 13. 44 14. 86 16. 76 19. 03 21. 58 24. 32 27. 17 30. 09 13. 58 13. 89 14. 59 15. 77 17. 43 19. 50 21. 89 24. 51 27. 28 30. 15 15 15. 05 15. 28 15. 82 16. 79 18. 21 20. 07 22. 28 24. 77 27. 44 30. 25 30

• What’s Best? Arthur T. Benjamin and Matthew T. Fluet, American Mathematical Monthly 107: 6 (2000), 560 -562.

Definition: The qth percentile is the number k for which P (X<k)<q/100 and P(X≤k)>q/100. The 50 th percentile is also called the median. Theorem (Benjamin, Fluet) Flipping a coin with probability of heads p, the configuration of n coins which has minimal expected time to remove all n is the pth percentile of the binomial distribution with parameters n and p. Proof. Flip the coin n times and let X be the number of heads.

Theorem (Benjamin, Fluet) Flipping a coin with probability of heads p, the configuration of n coins that wins over half the time against any other configuration is the median of the binomial distribution with parameters n and p. Illustration of proof (our case). Flip the coin n times. From the binomial distribution, P(X<6) 0. 350 P(X=6) 0. 273 P(X=7) 0. 234 P(X>7) 0. 143

• The Best Way to Knock ’m Down, Art Benjamin and Matthew Fluet, UMAP Journal 20: 1 (1999), 11 -20.

• The River Crossing Game, David Goering and Dan Canada, Mathematics Magazine 80: 1 (2007), 3 -15.

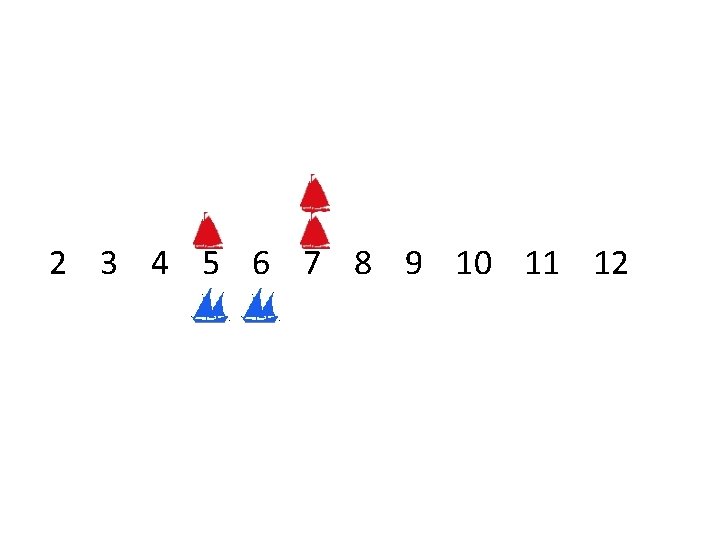
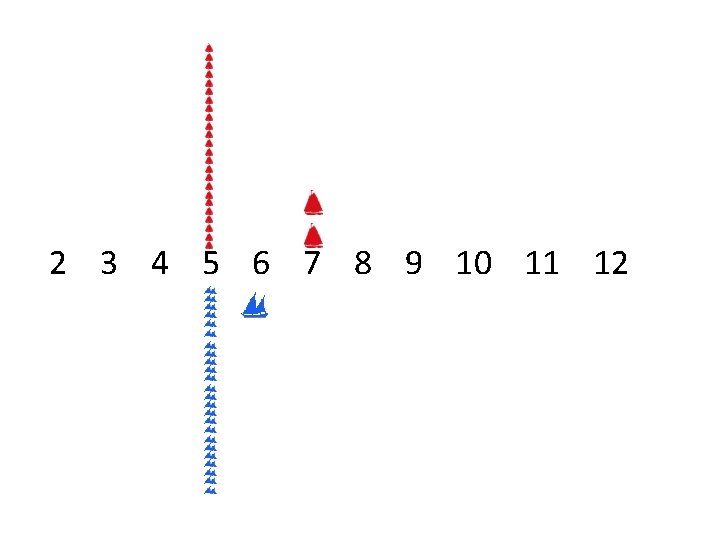
2 3 4 5 6 7 8 9 10 11 12

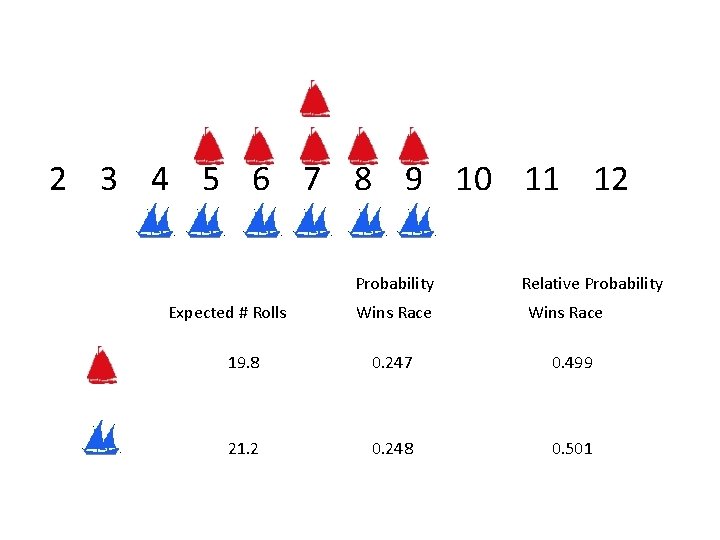
2 3 4 5 6 7 8 9 10 11 12 Probability Expected # Rolls Wins Race Relative Probability Wins Race 19. 8 0. 247 0. 499 21. 2 0. 248 0. 501

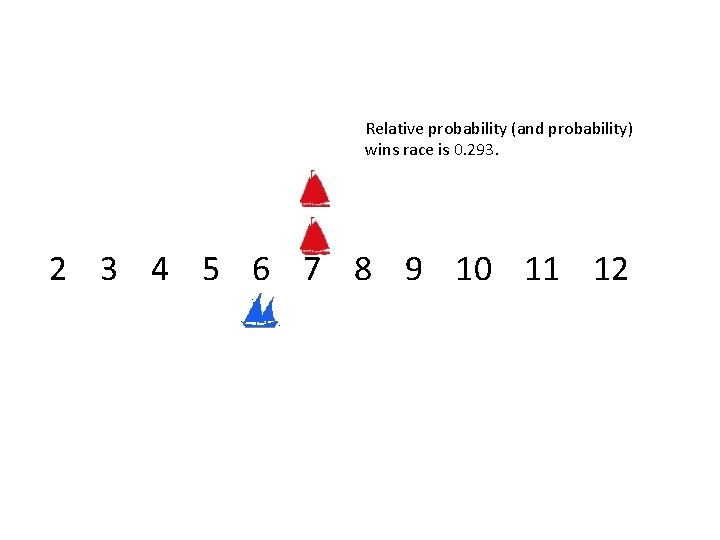
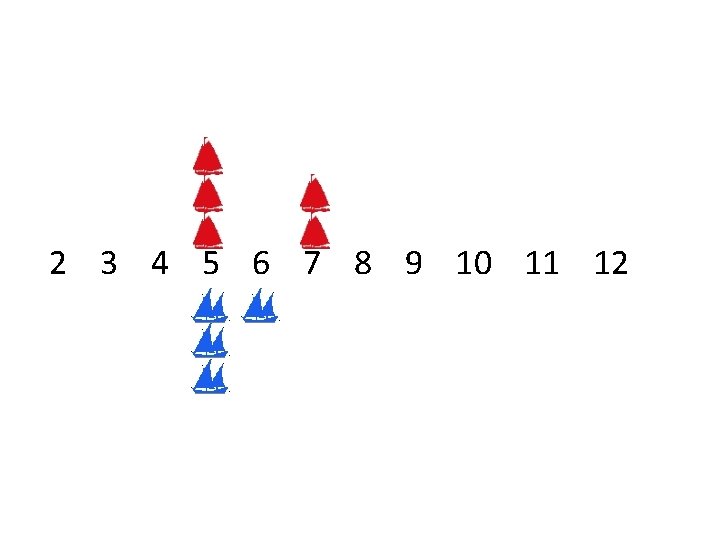
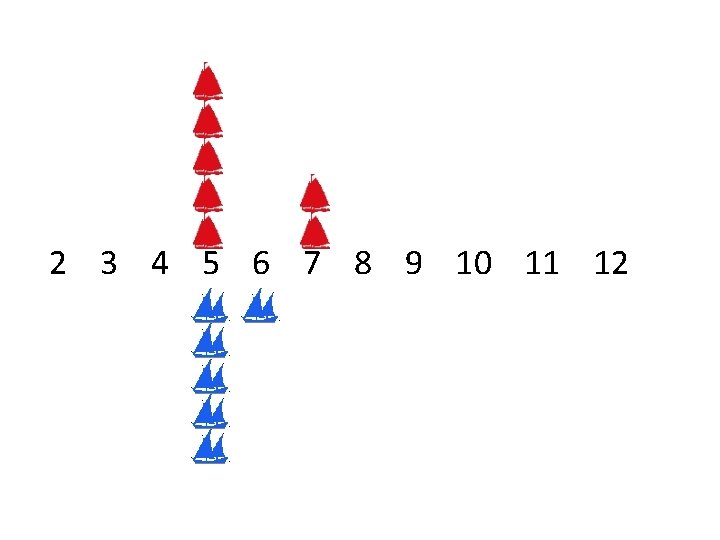
Relative probability (and probability) wins race is 0. 293. 2 3 4 5 6 7 8 9 10 11 12

2 3 4 5 6 7 8 9 10 11 12

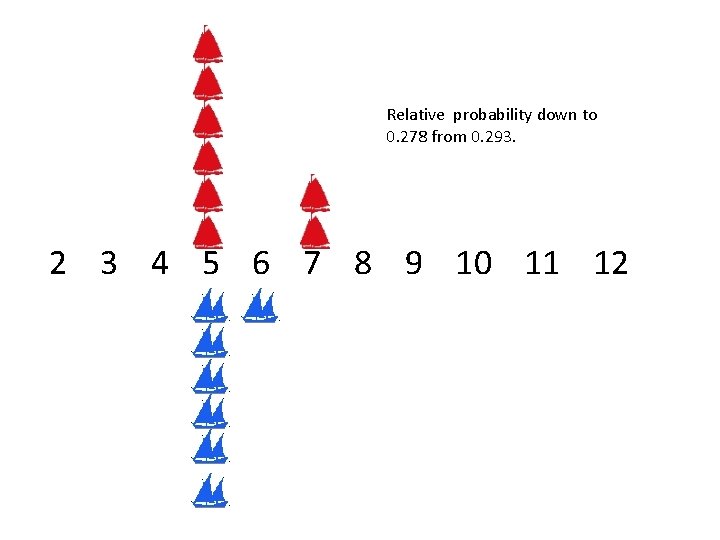
Relative probability down to 0. 278 from 0. 293. 2 3 4 5 6 7 8 9 10 11 12

2 3 4 5 6 7 8 9 10 11 12

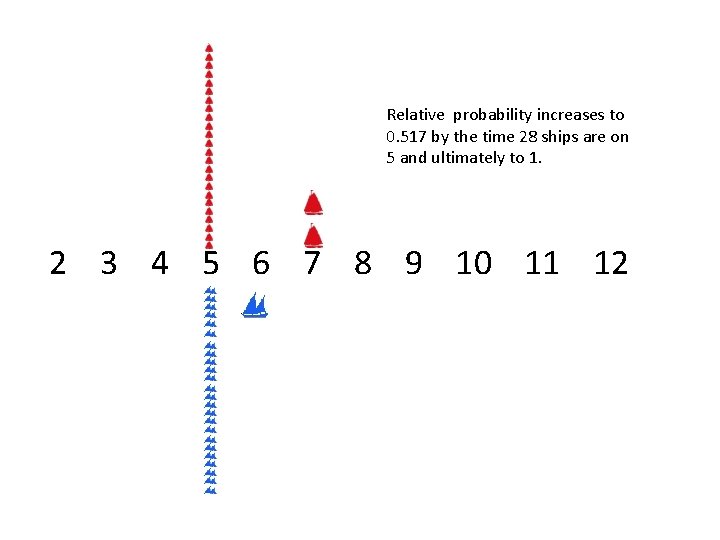
Relative probability increases to 0. 517 by the time 28 ships are on 5 and ultimately to 1. 2 3 4 5 6 7 8 9 10 11 12

2 3 4 5 6 7 8 9 10 11 12

Relative probability is small and decreases at first, but ultimately increases to 1. 2 3 4 5 6 7 8 9 10 11 12

• Waiting Times for Patterns and a Method of Gambling Teams, Vladimir Pozdnyakov and Martin Kulldorff, American Mathematical Monthly 133: 2 (2006), 134 -143. • A Martingale Approach to the Study of Occurrence of Sequence Patterns in Repeated Experiments, Shuo-Yen Robert Li, The Annals of Probability 8: 6 (1980), 1171 -1176.

HTHH vs HHTT

HTHH vs HHTT • Which happens fastest on average? • Which is more likely to win a race?

Expected Number of Flips to See the Sequence 30 HHHH 20 HTHT 18 HTHH HHTH HTTH 16 HHTT HHHT HTTT

• The expected duration for sequences with more than two outcomes and not necessarily equal probabilities, e. g. a loaded die, is still • For different sequences R and S, not necessarily of the same length, still makes computational sense. S is the one sliding; order matters!

• The expected time to hit a sequence S given a head start R (not necessarily all useful) is

Racing sequences S 1, …, Sn • Probabilities of winning p 1, …, pn • Expected number of flips E

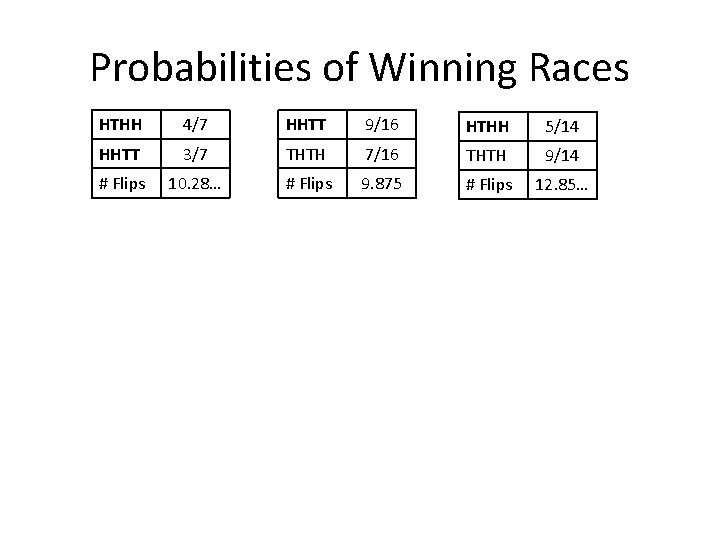
Probabilities of Winning Races HTHH 4/7 HHTT 3/7 # Flips 10. 28… Yet the expected number of flips to get HTHH is 18, versus 16 to get HHTT.

Probabilities of Winning Races HTHH 4/7 HHTT 9/16 HHTT 3/7 THTH 7/16 # Flips 10. 28… # Flips 9. 875

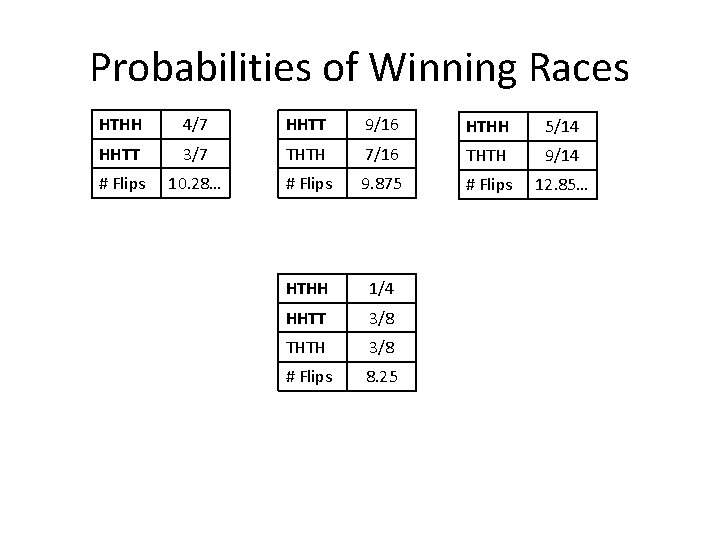
Probabilities of Winning Races HTHH 4/7 HHTT 9/16 HTHH 5/14 HHTT 3/7 THTH 7/16 THTH 9/14 # Flips 10. 28… # Flips 9. 875 # Flips 12. 85…

Probabilities of Winning Races HTHH 4/7 HHTT 9/16 HTHH 5/14 HHTT 3/7 THTH 7/16 THTH 9/14 # Flips 10. 28… # Flips 9. 875 # Flips 12. 85… HTHH 1/4 HHTT 3/8 THTH 3/8 # Flips 8. 25