Ordnung und Chaos im Sonnensystem Peter H Richter

Ordnung und Chaos im Sonnensystem Peter H. Richter Vortrag im Deutschen Zentrum für Luft- und Raumfahrt Bremen 22. Februar 2010 Peter H. Richter 1

Keplers Ordnung Johannes Kepler 1571 -1630 Mysterium Cosmographicum 1597 Astronomia Nova 1609 1990 -2005 Ellipsen Harmonices Mundi 1619 Peter H. Richter 2

• • • Geschichte Deterministisches Chaos Das eingeschränkte Dreikörperproblem Ist das Sonnensystem mechanisch stabil? Zusammenfassung Peter H. Richter 3

Meister aus 300 Jahren I. Newton H. Poincaré Oskar II L. Euler G. D. Birkhoff J. de Lagrange P. S. de Laplace C. G. J. Jacobi E. Strömgren A. N. Kolmogorov V. I. Arnold Strömgren. Peter H. Richter Chirikov J. Moser 4

Preisfrage von König Oskar II. 1888 Für ein gegebenes System von n sich untereinander anziehenden Teilchen, die den Newtonschen Bewegungsgesetzen folgen, soll unter der Annahme, dass es zu keinem Zweierstoß kommt, eine allgemeine Lösung gefunden werden in Form einer Potenzreihe in den Zeit und Raumkoordinaten, die für alle Werte der Zeit und Raum Koordinaten gleichförmig konvergiert. zurück Peter H. Richter 5

Strömgrens periodische Bahnen 1925 zurück Peter H. Richter 6

Deterministisches Chaos • Standard-Abbildung B. V. Chirikov Standard-Abbildung • Poincaré-Birkhoff: rationale Tori → Paare von Resonanzen, stabile elliptische Orbits und instabile hyperbolische • Kolmogorov-Arnold-Moser: hinreichend irrationale Tori überleben Peter H. Richter 7

Die zahlentheoretische Bedingung Kettenbruchentwicklung gibt die besten rationalen Näherungen Beste Approximation bis zu Nennern qn Geht es auch umgekehrt? C. L. Siegel J. Liouville Peter H. Richter 8

Die irrationalsten Zahlen Goldener Schnitt g = 1/(1+g): kleinstes t, größtes c' Alle noblen Zahlen w = [w 0, …, wn, 1, 1, 1, …] haben dieselben t, c'. Quadratische Irrationalzahlen: periodische Kettenbrüche, t = 2. Algebraische Zahlen vom Grad k haben t = k. Peter H. Richter 9

Das eingeschränkte Dreikörperproblem • Zwei Hauptkörper (Sonne und Jupiter) auf Kreisbahnen • Ein „infinitesimal kleiner“ dritter Körper in derselben Ebene • Zwei Bezugssysteme: ein ruhendes und ein mitrotierendes Poincaré-Schnitte Bezugssysteme • „Energie“ im mitrotierenden System E = E 0 – w · L 0 (Jacobi-Konstante) • Windungszahl im Kepler-Grenzfall W = 1 – T/Tj = 1 – a 3/2 • „Störung“: Jacobi-Potential Peter H. Richter 10

Jacobi-Potential 0. 5 0. 1 0. 000 03 0. 000 003 Peter H. Richter 11

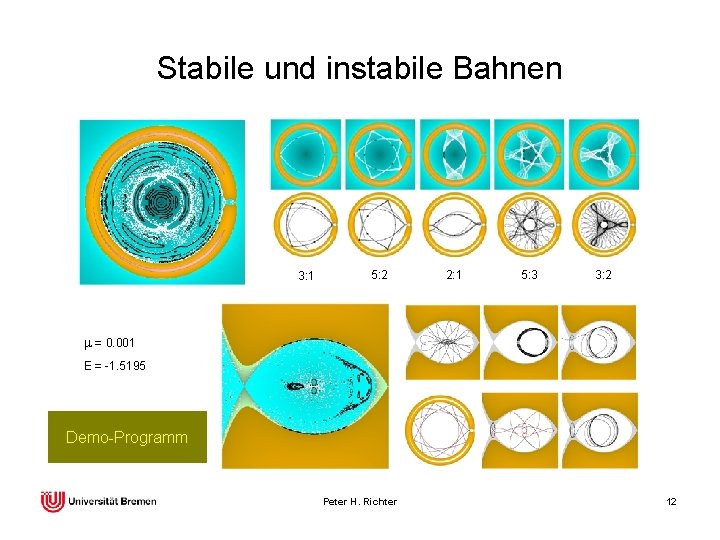
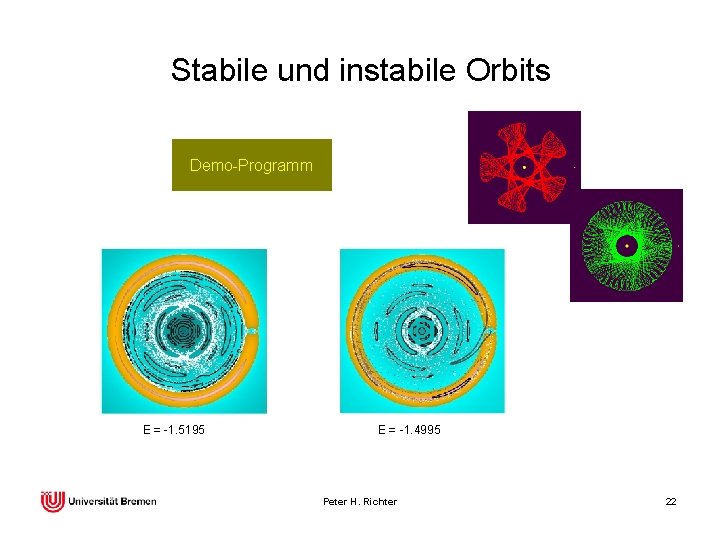
Stabile und instabile Bahnen 3: 1 5: 2 2: 1 5: 3 3: 2 m = 0. 001 E = -1. 5195 Demo-Programm Peter H. Richter 12

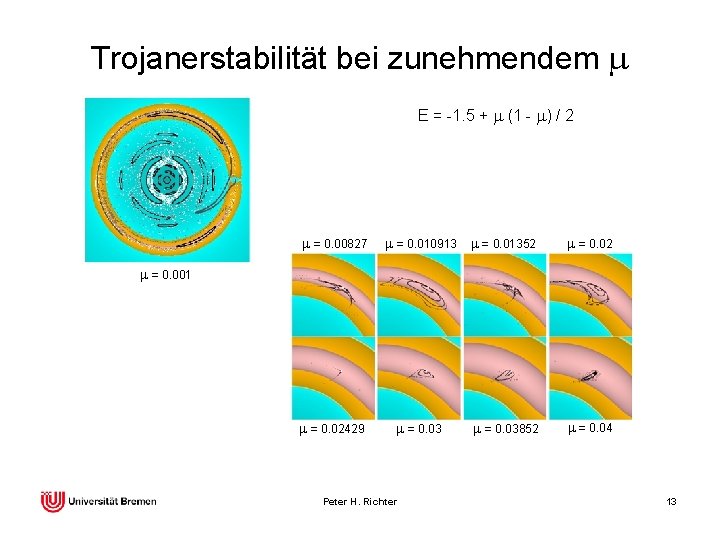
Trojanerstabilität bei zunehmendem m E = -1. 5 + m (1 - m) / 2 m = 0. 00827 m = 0. 010913 m = 0. 01352 m = 0. 001 m = 0. 02429 m = 0. 03 Peter H. Richter m = 0. 03852 m = 0. 04 13

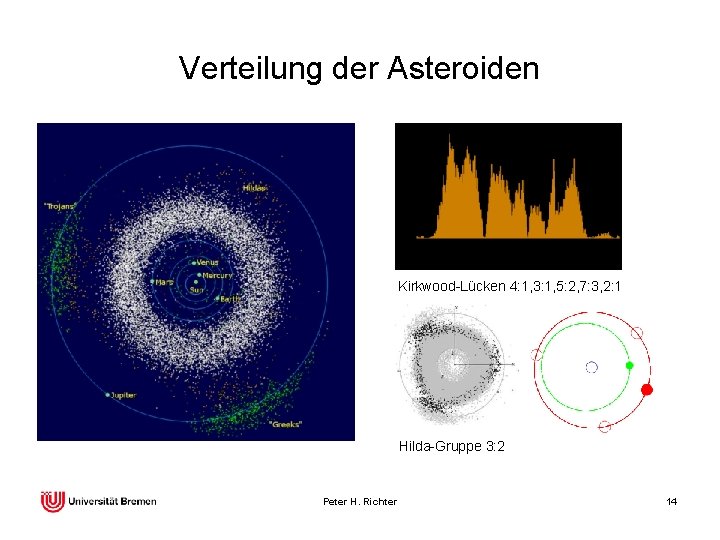
Verteilung der Asteroiden Kirkwood-Lücken 4: 1, 3: 1, 5: 2, 7: 3, 2: 1 Hilda-Gruppe 3: 2 Peter H. Richter 14

Gemeinsame Entfaltung von Ordnung und Chaos E = -1. 5195 E = -1. 4995 • Wachsendes E (und wachsendes m) verstärken Chaos und Ordnung • Chaos bedeutet: Stoß mit Jupiter oder Ejektion, jedenfalls Putzen • Ordnung bedeutet: Nähe zu einer stabilen Resonanz oder kontrolliert „irrationales“ Verhalten • Keplers harmonische Welt erscheint nun als Resultat einer Evolution Peter H. Richter 15

Poincaré-Schnitte in Polarkoordinaten • zeigen schön die Abhängigkeit von Jupiters Masse und der Energie • zeigen, welches Schicksal chaotische Bahnen früher oder später erleiden: Absturz oder Auswurf Peter H. Richter 16

Chaos schafft Ordnung: Keplers Harmonien? Peter H. Richter 17

Das ganze Sonnensystem incl. Dissipation alle 10 Körper Gezeitenkräfte und –reibung J. Wisdom Eigenrotation der Planeten J. Laskar Monde Stabile Resonanzen Resonanz-Katastrophen Fehler verzehnfachen sich etwa alle 10 Millionen Jahre Gezeitenreibung führte Merkur und die meisten Monde in stabile Resonanzen Viel kleinskaliges Chaos im Verhalten von Exzentrizitäten und Bahnneigungen Letzter Hit: parametrische Resonanz zwischen Jupiter und Merkur Peter H. Richter 18

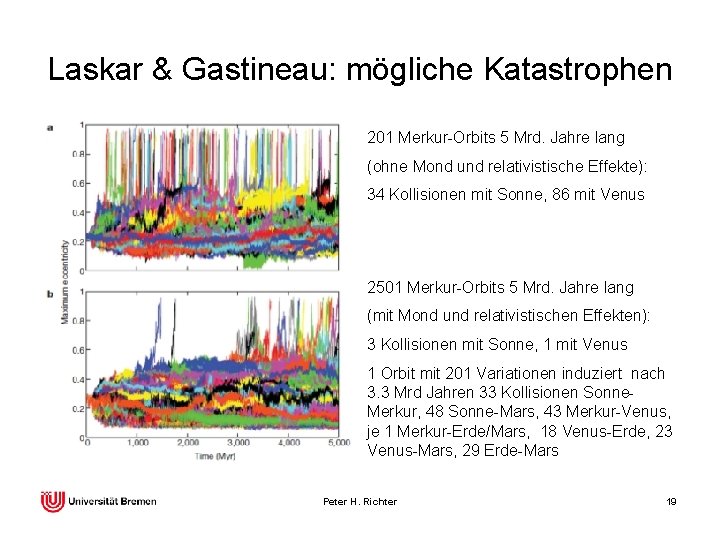
Laskar & Gastineau: mögliche Katastrophen 201 Merkur-Orbits 5 Mrd. Jahre lang (ohne Mond und relativistische Effekte): 34 Kollisionen mit Sonne, 86 mit Venus 2501 Merkur-Orbits 5 Mrd. Jahre lang (mit Mond und relativistischen Effekten): 3 Kollisionen mit Sonne, 1 mit Venus 1 Orbit mit 201 Variationen induziert nach 3. 3 Mrd Jahren 33 Kollisionen Sonne. Merkur, 48 Sonne-Mars, 43 Merkur-Venus, je 1 Merkur-Erde/Mars, 18 Venus-Erde, 23 Venus-Mars, 29 Erde-Mars Peter H. Richter 19

Zusammenfassung • Die mechanische Stabilität des Sonnensystems bleibt ungeklärt • Die Blätterung des hochdimensionalen Phasenraums in invariante Mengen, die unter dem Einfluss von Dissipation langsam evolvieren, ist ein hochkomplexes Gewebe regulärer und chaotischer Teile • Das Studium des eingeschränkten Dreikörperproblems mit nur 2 Freiheitsgraden gibt allenfalls eine Ahnung von dieser Komplexität • Es erlaubt immerhin das Studium interessanter Teilprobleme (Asteroidenverteilung, gebundene Rotation von Monden, parametrische Resonanz) • Extrasolare Planeten sind das nächste Anwendungsfeld Peter H. Richter 20

Peter H. Richter 21

Stabile und instabile Orbits Demo-Programm E = -1. 5195 E = -1. 4995 Peter H. Richter 22