Numerical approach to multiloop integrals K Kato Kogakuin

Numerical approach to multiloop integrals K. Kato (Kogakuin University) with E. de Doncker, N. Hamaguchi, T. Ishikawa, T. Koike, Y. Kurihara, Y. Shimizu, F. Yuasa The XXth International Workshop High Energy Physics and Quantum Field Theory September 25, 2011 Sochi, Russia

motivation • Theoretical prediction for High Energy Physics can be done by the perturbative calculation in Quantum Field Theory. (QFTHEP) • Sometimes important information comes from multi-body final states. Experimentalists presents (after hard work) high-statistic data. This requires higher order calculation. Large scale calculation is inevitable.

How to handle large scale computation? • It is beyond man-power. • Automated systems to perform perturbative calculation in QFT have been developed. • Many systems are successfully working in tree and 1 -loop level. GRACE, Comp. HEP, Calc. HEP, Feyn. Art/Calc, FDC, …

• Next generation of systems should manage 2 -loop and higher orders. • One of the essential components is the general multi-loop calculation library. • Formulae for 2 -loop integrals are given for many cases: However, it seems to be difficult to write ‘general solution’.

multi-loop integrals(scalar) Introduce Feynman parameters to combine denominators Integrate by loop momenta Polynomials of x’s: TARGET depends on masses and momenta

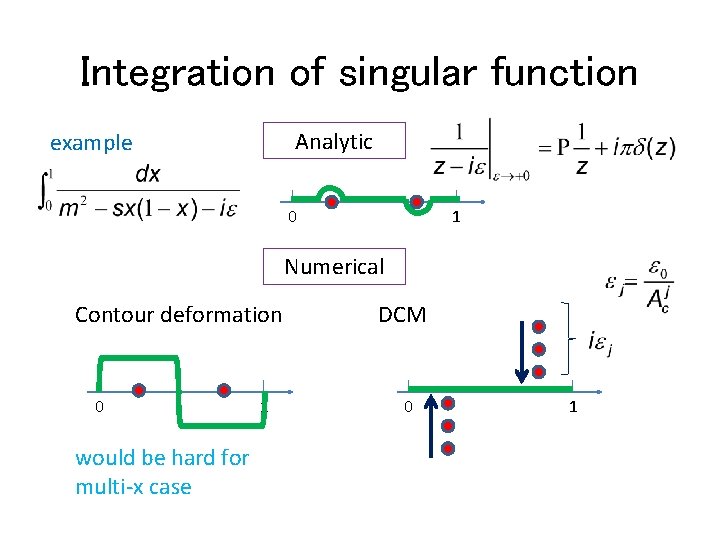
Integration of singular function Analytic example 0 1 Numerical Contour deformation 0 would be hard for multi-x case 1 DCM 0 1

Direct Computation Method(DCM) Target Simple example Analytic If D has no zero in the integration domain, take and perform numerical integration. If D has zero in the integration domain, we keep finite. Denominator is positive: Numerical evaluation is possible.

DCM(cont. ), extrapolation Wynn’s algorithm ( Math. magic) Even k terms give good estimation Input DCM= regularized integration + series extrapolation

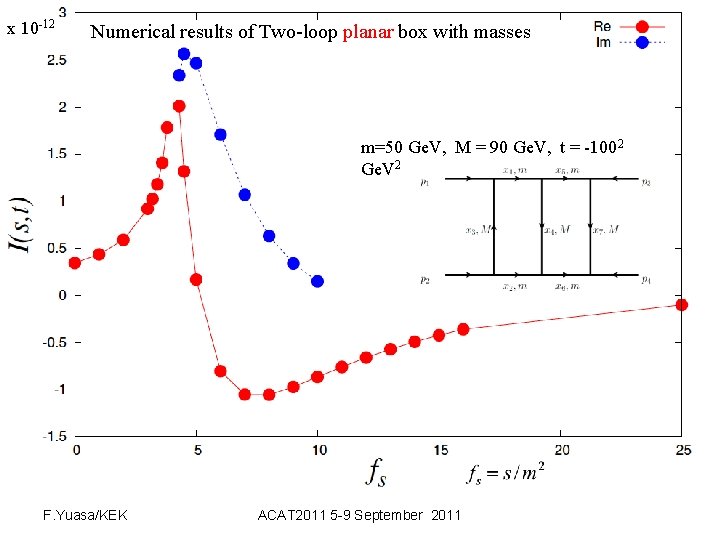
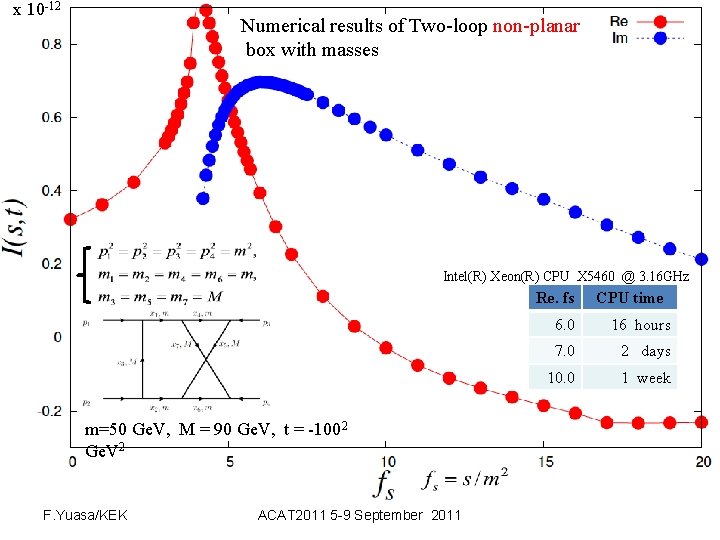
Examples: 2 -loop box (Yuasa) Following loop diagrams are successfully calculated by DCM. Mostly scalar integrals, but inclusion of numerator will be straightforward since DCM is based on numerical integration. 1 -loop : 3, 4, 5, 6 – point functions 2 -loop: 2, 3, 4 – point functions Following slides are the results for 2 -loop box.

x 10 -12 Numerical results of Two-loop planar box with masses m=50 Ge. V, M = 90 Ge. V, t = -1002 Ge. V 2 F. Yuasa/KEK ACAT 2011 5 -9 September 2011

x 10 -12 Numerical results of Two-loop non-planar box with masses Intel(R) Xeon(R) CPU X 5460 @ 3. 16 GHz Re. fs m=50 Ge. V, M = 90 Ge. V, t = -1002 Ge. V 2 F. Yuasa/KEK ACAT 2011 5 -9 September 2011 CPU time 6. 0 16 hours 7. 0 2 days 10. 0 1 week

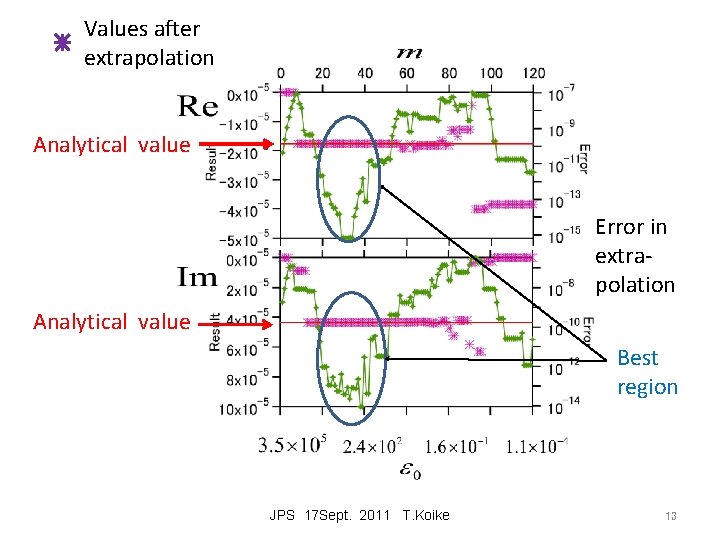
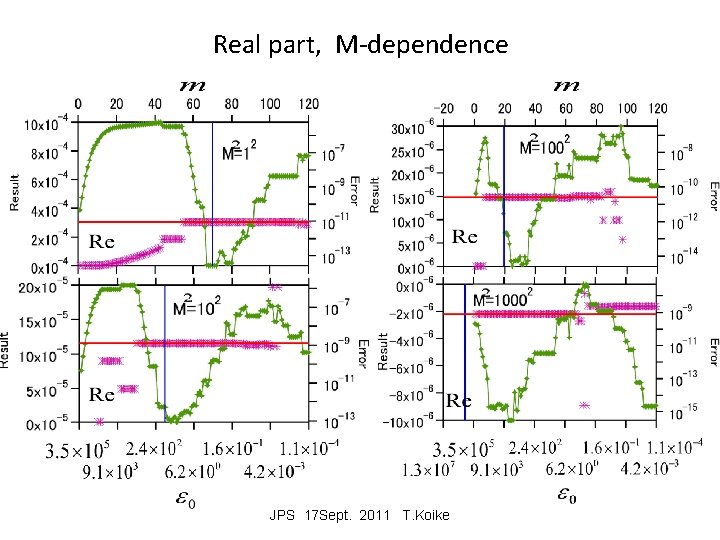
extrapolation control (Koike) The choice of epsilons Example Prepare integral values for m=0 and j=0 , . . , 140. The first term is of m=0, . . , 120. The 21 terms starting from j=m are the target of extrapolation.

Values after extrapolation Analytical value Error in extrapolation Analytical value Best region JPS 17 Sept. 2011 T. Koike 13

Real part, M-dependence JPS 17 Sept. 2011 T. Koike

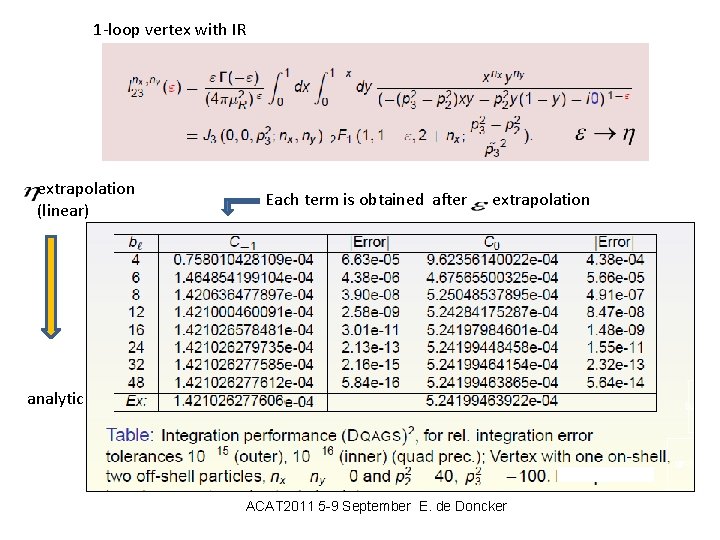
separation of singularity (de Donker) This integral might have IR divergence and/of UV divergence as pole(s) of. We need double extrapolation for both when V has zero in the integral region. Separation of IR poles is successful even for double-pole cases.

1 -loop vertex with IR extrapolation (linear) Each term is obtained after extrapolation analytic ACAT 2011 5 -9 September E. de Doncker

summary • Direct computation method(DCM) is a unique numerical method to calculate loop integrals for general masses and momenta. • Some items remain before it will become an important component in an automated system for higher order radiative corrections. - Study the validity of the method for wider class of mass configuration - Numerical handling of UV/IR divergence - Improve parameter selection technique for iterated computation - Accelerate computation using modern IT technology