NonEuclidean Geometries Steph Hamilton The Elements 5 Postulates

















- Slides: 21

Non-Euclidean Geometries Steph Hamilton

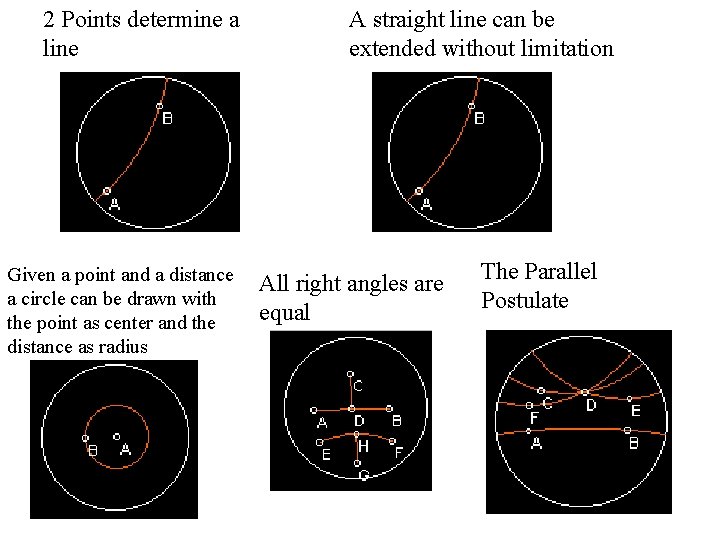
The Elements: 5 Postulates 1. To draw a straight line from any point to any other 2. Any straight line segment can be extended indefinitely in a straight line 3. To describe a circle with any center and distance 4. That all right angles are equal to each other 5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, if produced indefinitely, meet on that side on which are the angles less than the two right angles

Parallel Postulate 5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, if produced indefinitely, meet on that side on which are the angles less than the two right angles • Doesn’t say || lines exist!

Isn’t it a Theorem? • Most convinced it was • Euclid not clever enough? • 5 th century, Proclus stated that Ptolemy (2 nd century) gave a false proof, but then went on to give a false proof himself! • Arab scholars in 8 th & 9 th centuries translated Greek works and tried to prove postulate 5 for centuries

Make it Easier • Substitute statements: ü There exists a pair of similar non-congruent triangles. ü For any three non-collinear points, there exists a circle passing through them. ü The sum of the interior angles in a triangle is two right angles. ü Straight lines parallel to a third line are parallel to each other. ü There is no upper bound to the area of a triangle. ü Pythagorean theorem. ü Playfair's axiom(postulate)

John Playfair-18 th century • Through a point not on a given line, exactly one line can be drawn in the plane parallel to the given line. ØProclus already knew this! ØMost current geometry books use this instead of the 5 th postulate

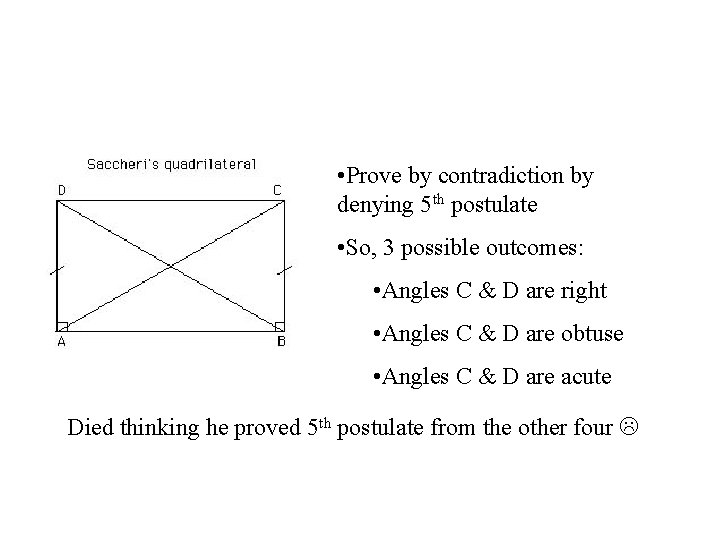
Girolamo Saccheri – early 18 th century • Italian school teacher & scholar • He approached the Parallel Postulate with these 4 statements: 1. Axioms contain no contradictions because of real-world models 2. Believe 5 th post. can be proved, but not yet 3. If it can be, replace with it’s negation, put contradiction into system 4. Use negation, find contradiction, show it can be proved from other 4 postulates w/o direct proof

2 Part Negation 1. There are no lines parallel to the given line • Euclid already proved that parallel lines exist using 2 nd postulate 2. There is more than one line parallel to the given line • Weak results, convinced almost no one

• Prove by contradiction by denying 5 th postulate • So, 3 possible outcomes: • Angles C & D are right • Angles C & D are obtuse • Angles C & D are acute Died thinking he proved 5 th postulate from the other four

New Plane Geometry Can there be a system of plane geometry in which, through a point not on a line, there is more than one line parallel to the given line? • Gauss was 1 st to examine at age 15. “In theory of parallels we are even now not further than Euclid. This is a shameful part of mathematics. ” • Never published findings

Can there be a system of plane geometry in which, through a point not on a line, there is more than one line parallel to the given line? • Gauss worked with Farkas Bolyai who also made several false proofs. • Farkas taught his son, Janos, math, but advised him not to waste one hour’s time on that problem. • 24 page appendix to father’s book • Nicolai Lobachevsky was 1 st to publish this different geometry • Together they basically came to the conclusion that the Parallel Postulate cannot be proven from the other four postulates

Lobachevskian Geometry • Roughly compared to looking down in a bowl • Changes 5 th postulate to, through a point not on a line, more than one parallel line exists • Called hyperbolic geometry because its playing field is hyperbolic • Poincare disk • Negative curvature: lines curve in opposite directions • Example of this geometry

2 Points determine a line Given a point and a distance a circle can be drawn with the point as center and the distance as radius A straight line can be extended without limitation All right angles are equal The Parallel Postulate

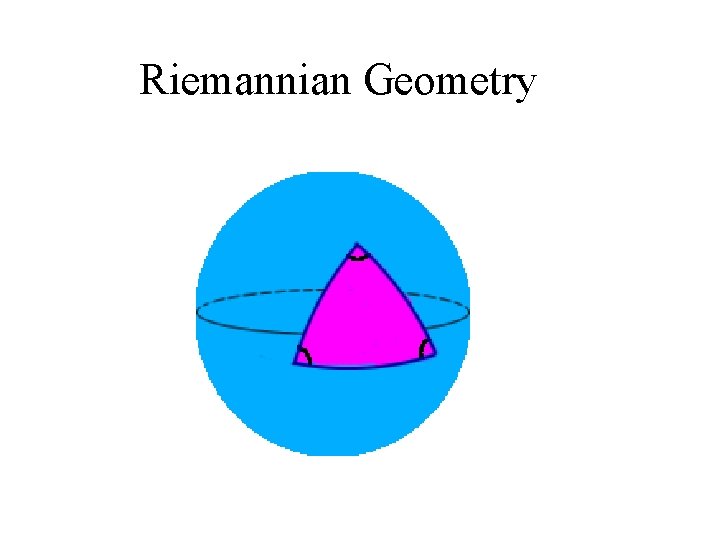
Riemannian Geometry • Bernhard Riemann – 19 th century • Looked at negation of 1 st part of Parallel Postulate “Can there be a system of plane geometry in which, through a point not on a line, there are no parallels to the given line? • Saccheri already found contradiction, but based on fact that straight lines were infinite • Riemann deduced that “extended continuously” did not mean “infinitely long”

Riemannian Geometry • Continue an arc on a sphere – trace over • New plane is composed great circles • Also called elliptical geometry • Positive curvature: lines curve in same direction

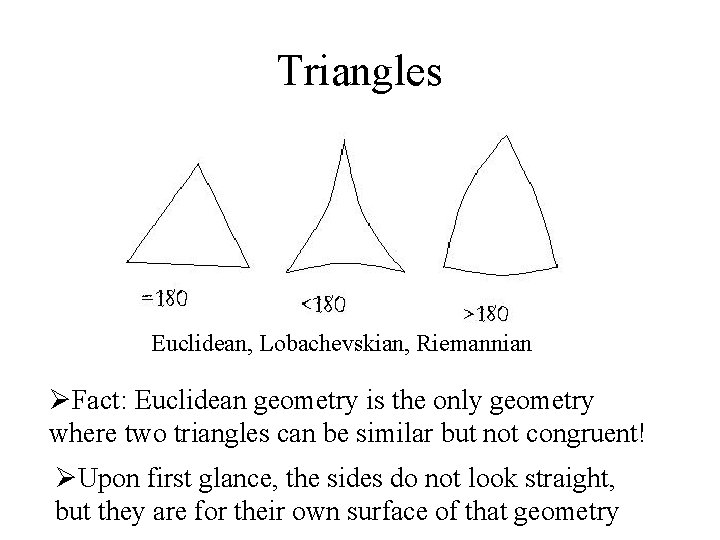
Triangles Euclidean, Lobachevskian, Riemannian ØFact: Euclidean geometry is the only geometry where two triangles can be similar but not congruent! ØUpon first glance, the sides do not look straight, but they are for their own surface of that geometry

Riemannian Geometry

C/D • Euclidean geometry, it is exactly pi • Lobachevskian, it is greater than pi • Riemannian, it is less than pi Pythagorean Thm • Euclidean: c 2=a 2 + b 2 • Lobachevskian: c 2>a 2 + b 2 • Riemannian : c 2< a 2 + b 2

Which one is right? Poincaré added some insight to the debate between Euclidean and non-Euclidean geometries when he said, “One geometry cannot be more true than another; it can only be more convenient”. • Euclidean if you are a builder, surveyor, carpenter • Riemannian if you’re a pilot navigating the globe • Lobachevskian if you’re a theoretical physicist or plotting space travel because outer space is thought to be hyperbolic “To this interpretation of geometry, I attach great importance, for should I have not been acquainted with it, I never would have been able to develop theory of relativity. ” ~Einstein

Timeline • • • Euclid’s Elements – 300 B. C. E. Ptolemy’s attempted proof – 2 nd century Proclus’s attempted proof-5 th century Arab Scholar’s translate Greek works – 8 th & 9 th centuries Playfair’s Postulate – 18 th century Girolamo Saccheri – 18 th century Carl Friedrich Gauss – 1810 Nicolai Lobachevsky – 1829 Janos Bolyai – 1832 Bernhard Riemann – 1854

References • http: //members. tripod. com/~noneuclidean/hyperbolic. html • http: //www-groups. dcs. st-and. ac. uk/~history/Hist. Topics/Non. Euclidean_geometry. html • http: //www. geocities. com/Cape. Canaveral/7997/noneuclid. html • http: //pegasus. cc. ucf. edu/~xli/non-euclid. htm • http: //www. mssm. org/math/vol 1/issue 1/lines. htm • http: //www. princeton. edu/~mathclub/images/euclid. jpg • http: //www. daviddarling. info/encyclopedia/N/non. Euclidean_geometry. html
 Steph hamilton
Steph hamilton Vsepr theory angles
Vsepr theory angles Steph subanidja
Steph subanidja Steph westwood writing program
Steph westwood writing program Steph westwood writing program
Steph westwood writing program By steph
By steph Steph subanidja
Steph subanidja Definition opposite rays
Definition opposite rays Postulates of kinetic molecular theory
Postulates of kinetic molecular theory Kmt postulates
Kmt postulates General relativity vs special relativity
General relativity vs special relativity What is microbiology
What is microbiology Drude theory of metals
Drude theory of metals Jural postulates of roscoe pound
Jural postulates of roscoe pound Pasteurized milk meaning
Pasteurized milk meaning Postulates of magnetostatics
Postulates of magnetostatics List of theorem
List of theorem Postulates of special theory of relativity
Postulates of special theory of relativity Postulates of thermodynamics
Postulates of thermodynamics Lesson 2 segments and rays
Lesson 2 segments and rays Define animalcules in microbiology
Define animalcules in microbiology Example of aa similarity theorem
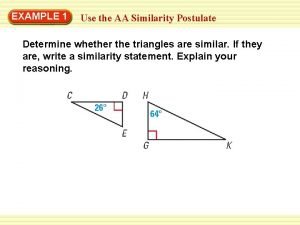
Example of aa similarity theorem