NONEUCLIDEAN GEOMETRIES Austin Mahlum SPACE MAP v 4

NON-EUCLIDEAN GEOMETRIES Austin Mahlum

SPACE MAP v 4 Common Axioms v Euclidean Geometry v Saccheri Quadrilaterals v Birth of new geometries v Logical Consistency v Elliptic Geometry v Hyperbolic Geometry v Why should we study different geometries?

4 COMMON AXIOMS v 1. To draw a straight line from any point to any point. v 2. To produce [extend] a finite straight line continuously in a straight line. v 3. To describe a circle with any center and distance [radius]. v 4. That all right angles are equal to one another.

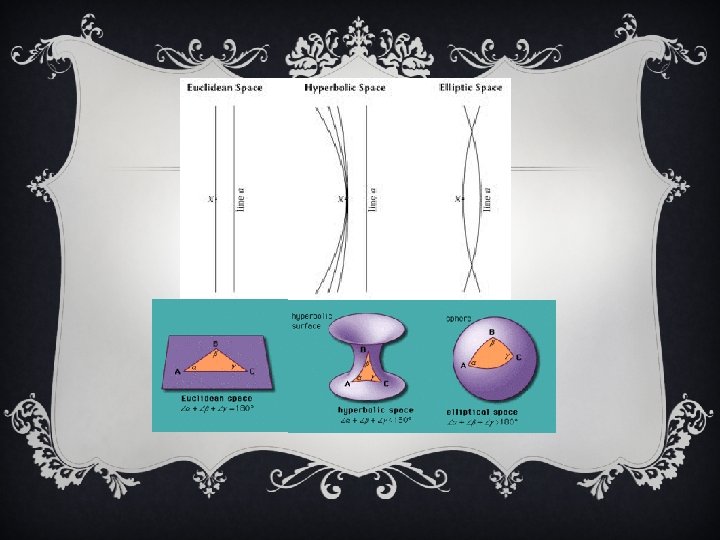
EUCLIDEAN GEOMETRY v Also known as parabolic geometry v What we are taught in high school v 5 th postulate: Given any straight line and a point not on it, there “exists one and only one straight line which passes” through that point and never intersects the first line, no matter how far they are extended. v Interior angle sum of a triangle is = 180 degrees. This is better known as the triangle postulate and is equivalent to the 5 th postulate.

SACCHERI QUADRILATERALS v Girolamo Saccheri(1667 -1733)- Attempts to use proof by contradiction to prove the triangle postulate, ends up with the Saccheri quadrilaterals.

BIRTH OF NEW GEOMETRIES v Carl Gauss (1777 -1855): Never published any formal work on the matter, but had private letters that showed he was working on it. v Nikolai Lobachevsky (1792 -1856): In 1829 published “On the Principles of Geometry”. v Janos Bolyai (1802 -1860): In 1832 published “The Science of Absolute Space”. v Georg Riemann (1826 -1866): In 1867 his work “On the Hypotheses which lie at the Bases of Geometry” was published.

LOGICAL CONSISTENCY v Eugenio Beltrami (1835 -1899): In 1868 published two memoirs that created models that were developed using Euclidean space as opposed to axiomatic fashion; however, these models worked with Non-Euclidean geometries. As a result, if these new geometries were not logically consistent, then Euclidean geometry was not consistent.

VISUAL AID

ELLIPTIC GEOMETRY v Also known as Riemannian geometry v Simplest model is a sphere v 5 th postulate: Given any straight line and a point not on it, there “exists no straight line which passes” through that point and never intersects the first line, no matter how far they are extended.

ELLIPTIC GEOMETRY v

HYPERBOLIC GEOMETRY v Also known as Lobachevsky-Bolyai-Gauss geoemetry v Simplest model is a pseudosphere v 5 th postulate: Given any straight line and a point not on it, there “exists at least two straight lines which pass” through that point and never intersects the first line, no matter how far they are extended.

HYPERBOLIC GEOMETRY

HYPERBOLIC GEOMETRY v Proposition 23: To construct a rectilinear angle equal to a given rectilinear angle on a given straight line and at a point on it. v Theorem 1 -3: The angle sum of a triangle does not exceed 180 degrees. v Definition 1 -1: A lambert quadrilateral is a quadrilateral with 3 right angles. v Theorem 1 -6: In hyperbolic geometry, the fourth angle of a Lambert quadrilateral is acute, and each side adjacent to the acute angle is longer than the opposite side.

HYPERBOLIC GEOMETRY v Theorem 1 -8: Given two lines, if there exists a transversal which cuts the lines so as to form equal alternate interior angles or corresponding angles, then the lines are parallel with a common perpendicular. v Theorem 1 -9: If two lines have a common perpendicular, there exists transversals, other than the perpendicular, which cut the lines so as to form equal alternate interior angles (or equal corresponding angles). Moreover, the only transversals with this property are those which go through the point on that perpendicular which is midway between the lines.

WHY STUDY DIFFERENT GEOMETRIES? v We do not know if our universe is shaped with Euclidean geometry, in fact Albert Einstein’s General Theory of Relativity and modern day String Theory depend on noneuclidean geometry to function.

SOURCES v http: //www-history. mcs. st-and. ac. uk/Hist. Topics/Non. Euclidean_geometry. html v http: //jwilson. coe. uga. edu/MATH 7200/Non. Euclidean. Comp anion/Non. Euclidean. Companion. pdf v http: //lamington. wordpress. com/2010/04/10/hyperbolicgeometry-notes-2 -triangles-and-gauss-bonnet/