New Algorithms for Enumerating All Maximal Cliques Kazuhisa

New Algorithms for Enumerating All Maximal Cliques Kazuhisa Makino Osaka University JAPAN Takeaki Uno National Institute of Informatics, JAPAN 9/Jul/2004 SWAT 2004

Background Recently, Enumeration algorithms are interesting ・ There are still many unsolved nice problems (unlike to ordinal discrete algorithms) ・ Recent increase of computer power makes many enumeration problems practically solvable many applications have been appearing, such as, genome, data mining, clustering, so on ・ Some (theoretical) algorithms use enumeration as subroutines (recognition of perfect graph)

Background (cont. ) ・ My institute has 100 researchers of informatics ・ At least 5 researchers (independently) use implementations of enumeration algorithms ・ Suppose that there are 100, 000 researchers of informatics in the world 5000 researchers use enumeration algorithms ? ? ?

Problems and Results Problem 1 : for a given graph G=(V, E), enumerate all maximal cliques in G Problem 2 : for a given bipartite graph G=(V 1∪V 2, E), enumerate all maximal bipartite cliques in G ( Problem 2 is a special case of Problem 1 ) ・ We propose algorithms for solving these problems, reduce the time complexity in dense cases and sparse cases. ・ Computational experiments for random graphs and real-world data

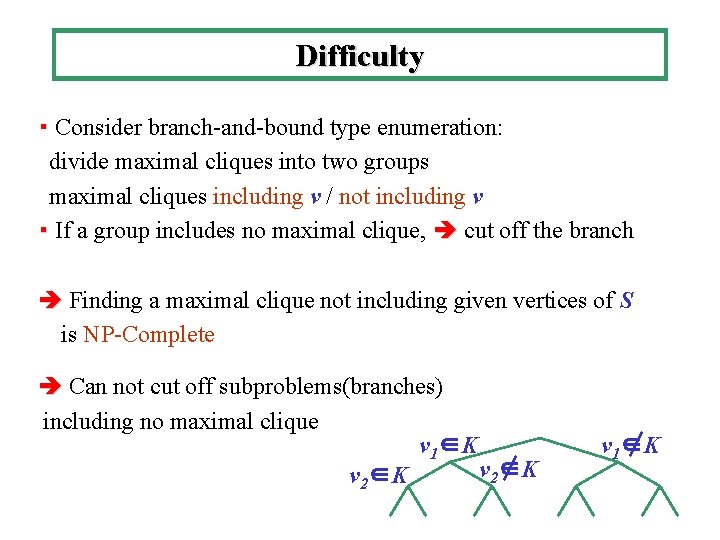
Difficulty ・ Consider branch-and-bound type enumeration: divide maximal cliques into two groups maximal cliques including v / not including v ・ If a group includes no maximal clique, cut off the branch Finding a maximal clique not including given vertices of S is NP-Complete Can not cut off subproblems(branches) including no maximal clique v 1∈K v 2∈K v 1∈K

Existing Studies and Ours O(|V||E|): Tsukiyama, Ide, Ariyoshi & Shirakawa, O(|V||E|), lexicographic order: Johnson, Yanakakis & Papadimitriou O(a(G)|E|): Chiba & Nishizeki ( a(G): arboricity of G with m/(n-1) ≦ a(G) ≦m 1/2 ) ・ many heuristic algorithms in data mining, for bipartite case Ours: O(|V|2. 376) (dense case) O(Δ 4) (sparse case) O((Δ*)4 + θ 3 ) (θ ( vertices have degree > Δ* ) O(Δ 3) (bipartite case) O(Δ 2) (bipartite case with using much memory)

Enumeration of Maximal Cliques ・ Improved version of algorithm of Tsukiyama et. al. Idea: Construct a route on all maximal cliques to be traversed ・ For a maximal clique K of G = ( V, E ) : C (K) : lexicographically maximum maximal clique including K K≦i : vertices of K with indices ≦ i i(K) : minimum index s. t. C(K≦i) = C(K≦i+1) parent of a maximal clique K : C(K≦i(K)-1) ・ parent is lexicographically larger than K 9 4 1 11 7 3 2 K 10 5 6 8 i(K) Lexicographically larger 1, 2, 3 > 1, 2, 4 1, 3, 6 > 1, 4, 5

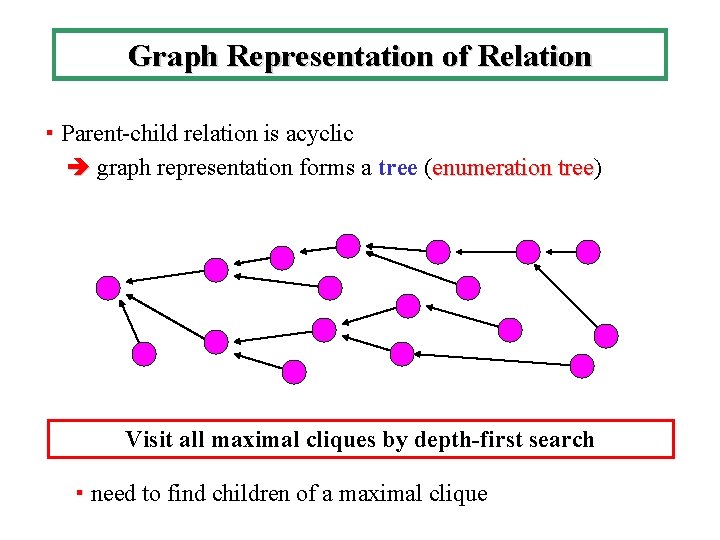
Graph Representation of Relation ・ Parent-child relation is acyclic graph representation forms a tree (enumeration tree) tree Visit all maximal cliques by depth-first search ・ need to find children of a maximal clique

Child of Maximal Clique Γ(vi) : vertices adjacent to vi K[i] = C ( K≦i ∩ Γ(vi) ∪ {vi} ) ・ H is a child of K only if H = K[i] for some i>i(K) (H is a child of K if the parent of K[i] is K ) ・ i(K[i]) = i K, i(K)=6 9 4 1 11 7 3 10 2 5 6 8 K[8] ・construct K[i] in O(|E|) time ・construct parent in O(|E|) time ( O(Δ 2 ) time) ・for i=i(K)+1, …, |V| in O(|V||E|) time enumerate O(|V||E|) time per maximal clique

Characterization of Child The parent of K[i] = K ⇔ (1) no vj , j<i is adjacent to all vertices in K≦i ∩Γ(vi) ∪ {vi} (2) no vj , j<i is adjacent to all vertices in K≦i∩Γ(vi) ∪ K≦j (1) is not satisfied ⇔ K[i] and parent of K[i] includes vj∈K (2) is not satisfied ⇔ parent of K[i] includes vj∈K 5 7 1 4 3 9 10 K = {3, 4, 7, 9} K[10] = {3, 7, 10} K≦ 5 = {3, 4} K ≦ 7∩Γ(v 10) = {3, 7} K≦ 5∪ K ≦ 10∩Γ(v 10) ∪ {v 10}

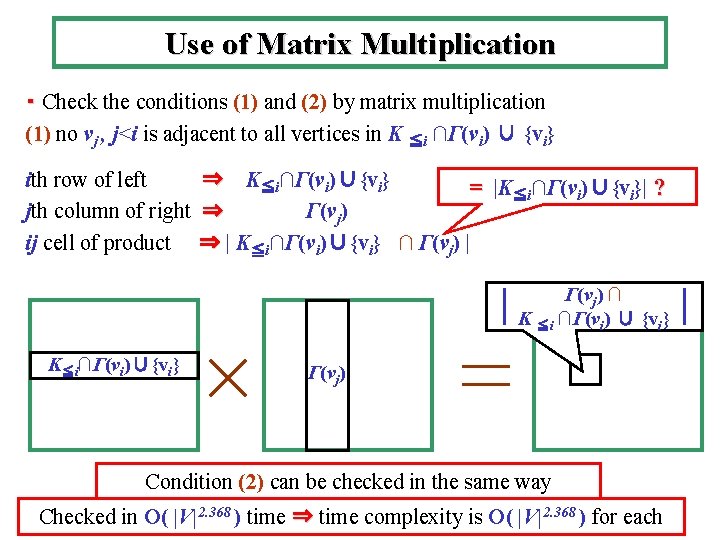
Use of Matrix Multiplication ・ Check the conditions (1) and (2) by matrix multiplication (1) no vj , j<i is adjacent to all vertices in K ≦i ∩Γ(vi) ∪ {vi} ith row of left ⇒ K≦i∩Γ(vi)∪{vi} = |K≦i∩Γ(vi)∪{vi}| ? jth column of right ⇒ Γ(vj) ij cell of product ⇒ | K≦i∩Γ(vi)∪{vi} ∩ Γ(vj) | Γ(vj) ∩ K ≦i ∩Γ(vi) ∪ {vi} K≦i∩Γ(vi)∪{vi} Γ(vj) Condition (2) can be checked in the same way Checked in O( |V|2. 368 ) time ⇒ time complexity is O( |V|2. 368 ) for each

Sparse Cases ・ If vi is adjacent to no vertex in K K[i] = C ( K≦i ∩ Γ(vi) ∪ {vi} ) = C ({vi}) parent of K[i] = C ({vi}) ≦i ) If C ({vi}) ≦i ＝φ, parent of K[i] is K 0 If C ({vi}) ≦i ≠φ, (1) is not satisfied If K ≠ K 0, K[i] is not a child of K Δ: max. degree ・ Since |K|≦Δ+1 , at most Δ(Δ+1) vertices are adjacent to K ・ Each K[i] takes O(Δ 2) time to construct the parent O(Δ 4 ) per maximal clique O((Δ*)4 + |Θ|3 ) if partially dense Δ*: max. degree in V＼Θ

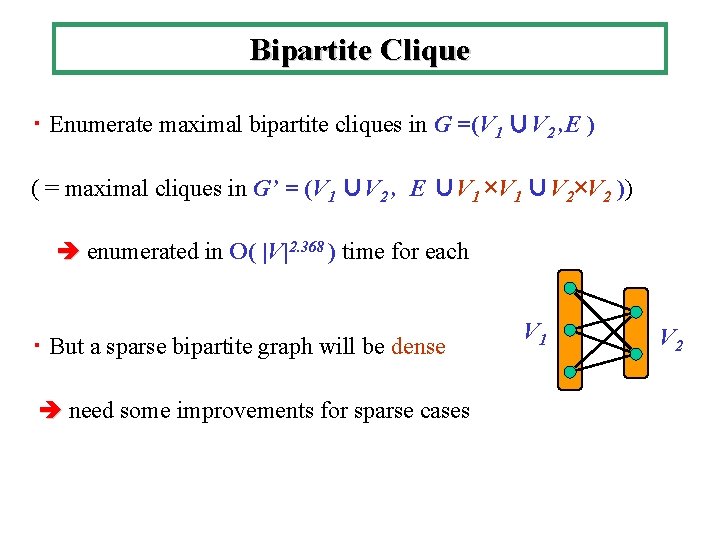
Bipartite Clique ・ Enumerate maximal bipartite cliques in G =(V 1 ∪V 2 , E ) ( = maximal cliques in G’ = (V 1 ∪V 2 , E ∪V 1 ×V 1 ∪V 2×V 2 )) enumerated in O( |V|2. 368 ) time for each ・ But a sparse bipartite graph will be dense need some improvements for sparse cases V 1 V 2

Fast Construction of K[i] ・ For any maximal bipartite clique K K ∩V 2 = ∩v∈K ∩V 1 Γ(v) K ∩V 1 = ∩v∈K ∩V 2 Γ(v) K[v 1] ・ K[i]∩V 1 for all i are computed in O(Δ 2) time ・ K[i] for all i are computed in O(Δ 3) time v 1 v 2 v 5 v 6 K[i] V 1 V 2 1 2 3 K[v 6] Γ(1) 4 vi Γ(2) Γ(3) Γ(4)

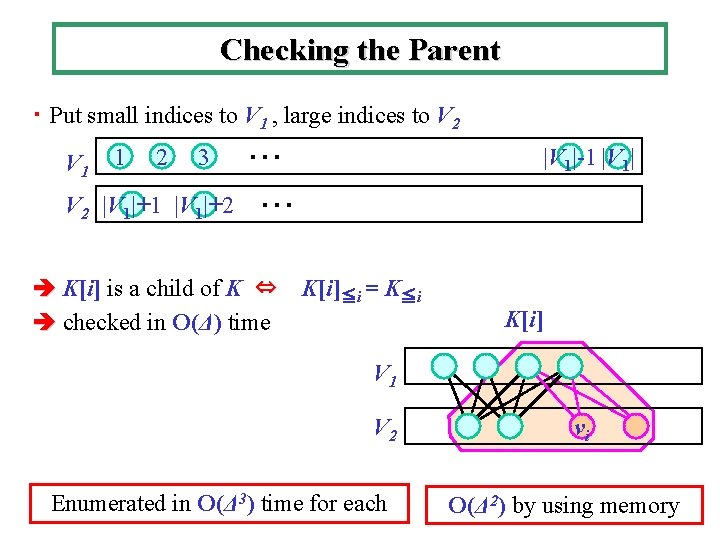
Checking the Parent ・ Put small indices to V 1 , large indices to V 2 V 1 1 2 3 V 2 |V 1|+1 |V 1|+2 |V 1|-1 |V 1| ・・・ K[i] is a child of K ⇔ K[i]≦i = K≦i checked in O(Δ) time K[i] V 1 V 2 Enumerated in O(Δ 3) time for each vi O(Δ 2) by using memory

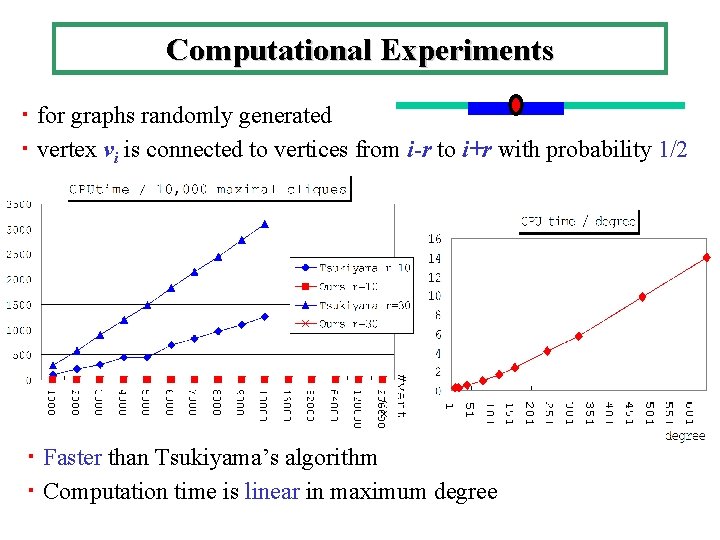
Computational Experiments ・ for graphs randomly generated ・ vertex vi is connected to vertices from i-r to i+r with probability 1/2 ・ Faster than Tsukiyama’s algorithm ・ Computation time is linear in maximum degree

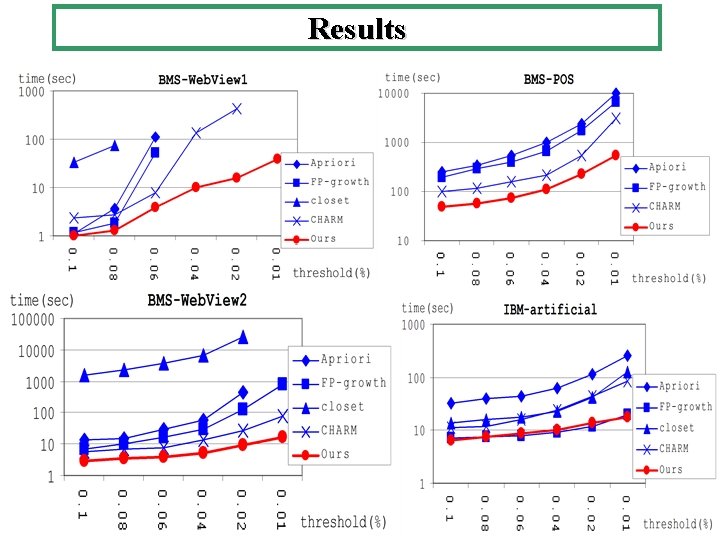
Benchmark Problems ・ Problem of finding frequent closed item sets from database equivalent to maximal bipartite clique enumeration ・ Used on KDDcup (data mining algorithm competition ) BMS-Web. View 1 (from Web-log data) |V|= 60, 000, ave. degree 2. 5 BMS-Web. View 2 (from Web-log data) |V|= 80, 000, ave. degree 5 BMS-POS (from POS data) |V|= 510, 000, ave. degree 6 IBM-Artificial (artificial data) |V|= 100, 000 , ave. degree 10

Results

Conclusion and Future Work ・ Proposed fast algorithms for enumerating maximal cliques: O(|V|2. 376), O(Δ 4 ), O((Δ*)4 + θ 3 ) maximal bipartite cliques: O(|V|2. 376), O(Δ 3 ), O(Δ 2) ・ Examined benchmark problems of data mining, and showed that our algorithm performs well. Future work: ・ Can we improve more? What is the difficulty ? ・ Can we enumerate other maximal (minimal) graph objects ? ・ Can we apply matrix multiplication to other enumeration problems ? ・ What can be enumerated efficiently in practice ?

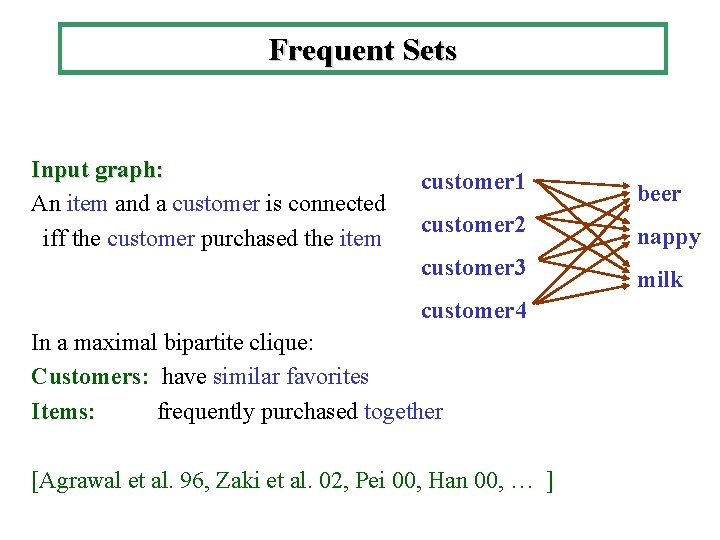
Frequent Sets Input graph: An item and a customer is connected iff the customer purchased the item customer 1 beer customer 2 nappy customer 3 milk customer 4 In a maximal bipartite clique: Customers: have similar favorites Items: frequently purchased together [Agrawal et al. 96, Zaki et al. 02, Pei 00, Han 00, … ]

Few Large Degree Vertices ・ Very few vertices (denoted by Θ) have large degrees small degree < Δ’ ・ Divide the maximal cliques into two groups: (a) cliques not included in Θ (b) cliques included in Θ ・ (a) can be enumerated in O(Δ’ 4) time ・ Maximal clique K in the induced graph by Θ is a maximal clique of G ⇔ K is not included in any of (a) O(|Θ|3) time for each O(Δ’ 4 + |Θ|3 ) per maximal clique large degree

Avoid Duplications by Using Memory ・We can avoid duplications by storing all maximal bipartite cliques ・ From K ∩V 1 =Γ(K ∩V 2) , we store all K ∩V 1 1. Get a K from memory (which is un-operated) 2. generate all K[i]∩V 1 3. Store each K[i]∩V 1 if it is not in memory 4. Go to 1 if a maximal clique is un-operated Enumerated in O(Δ 2) time for each