An Efficient Algorithm for Enumerating Pseudo Cliques Takeaki

An Efficient Algorithm for Enumerating Pseudo Cliques Takeaki Uno National Institute of Informatics & The Graduate University for Advanced Studies Dec/18/2007 ISAAC, Sendai

Introducing Pseudo Cliques

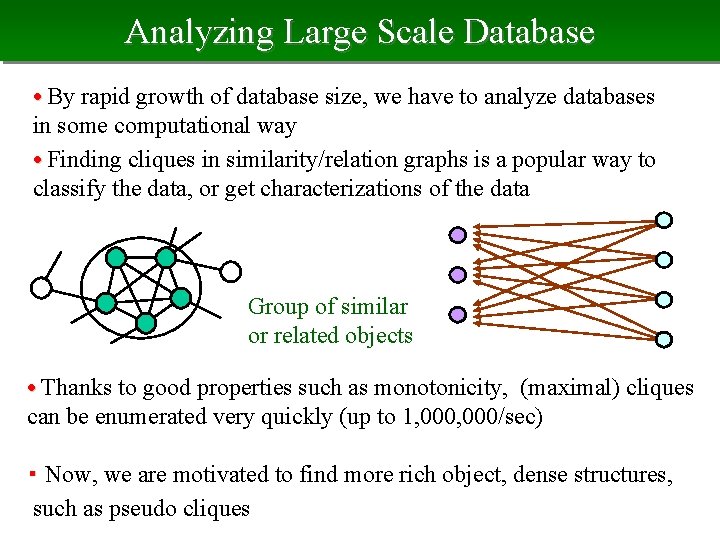
Analyzing Large Scale Database • By rapid growth of database size, we have to analyze databases in some computational way • Finding cliques in similarity/relation graphs is a popular way to classify the data, or get characterizations of the data Group of similar or related objects • Thanks to good properties such as monotonicity, (maximal) cliques can be enumerated very quickly (up to 1, 000/sec) ・ Now, we are motivated to find more rich object, dense structures, such as pseudo cliques

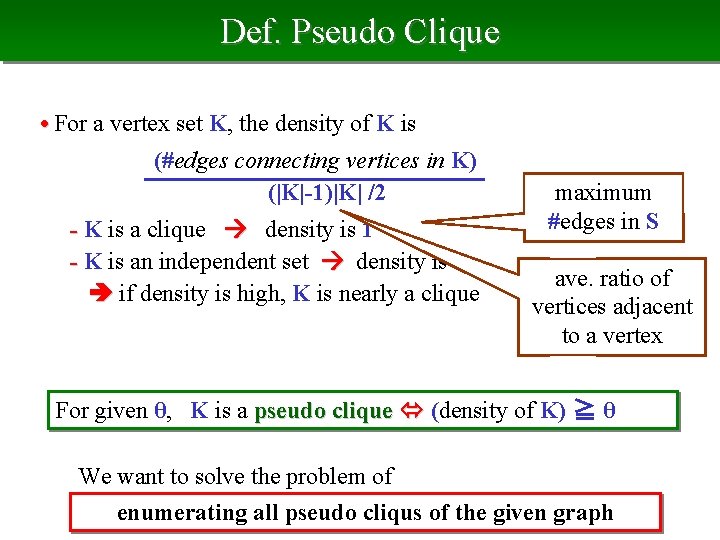
Def. Pseudo Clique • For a vertex set K, the density of K is (#edges connecting vertices in K) (|K|-1)|K| /2 - K is a clique density is 1 - K is an independent set density is 0 if density is high, K is nearly a clique maximum #edges in S ave. ratio of vertices adjacent to a vertex For given θ, K is a pseudo clique (density of K) ≧ θ We want to solve the problem of enumerating all pseudo cliqus of the given graph

Existing Results • Easy to find one pseudo clique two connected vertices always form a pseudo clique • Finding a pseudo clique of size k is NP-complete Reducing k-clique problem by setting θ= 1 • Approximation algorithms for maximizing the density for size k - O(|V|1/3 -ε) approaximation algorithm - O((n/k)ε) approx. if optimal solution is dense [Tokuyama el al. ] - PTAS if Ω(n 2) edges [Arora et al. ] • Many heuristic algorithms in data mining, data engineering, natural sciences • However, no algorithm for "complete" enumeration

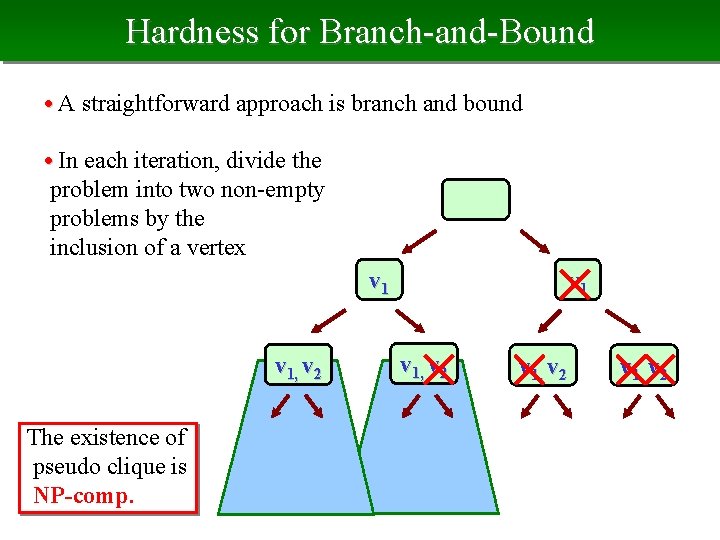
Hardness for Branch-and-Bound • A straightforward approach is branch and bound • In each iteration, divide the problem into two non-empty problems by the inclusion of a vertex 　　　 v 1, v 2 The existence of pseudo clique is NP-comp. v 1, v 2

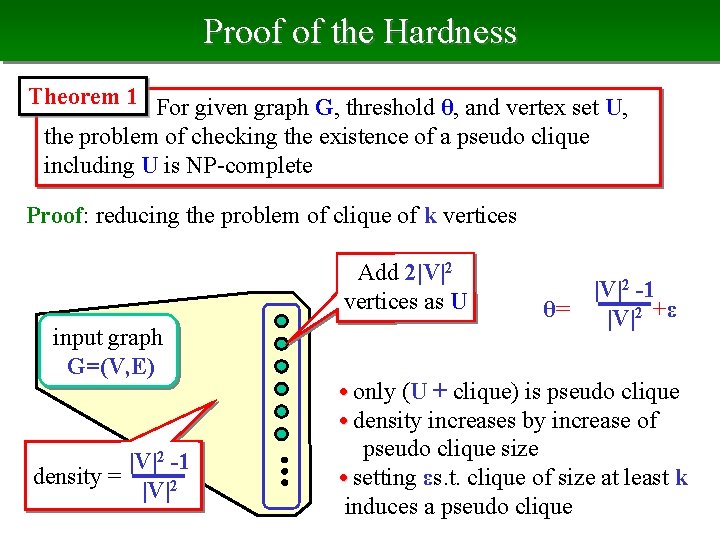
Proof of the Hardness Theorem 1 　　　　　　　For given graph G, threshold θ, and vertex set U, the problem of checking the existence of a pseudo clique including U is NP-complete Proof: reducing the problem of clique of k vertices Add 2|V|2 vertices as U input graph G=(V, E) |V|2 -1 density = |V|2 θ= |V|2 -1 |V|2 +ε • only (U + clique) is pseudo clique • density increases by increase of pseudo clique size • setting εs. t. clique of size at least k induces a pseudo clique

Is This Really Hard? • We proved NP-hardness for "very dense graphs" unclear for middle dense graph possibility for polynomial time enumeration θ= 1 easy θ= 0 hard ? ? ?

Polynomial Time Enumeration

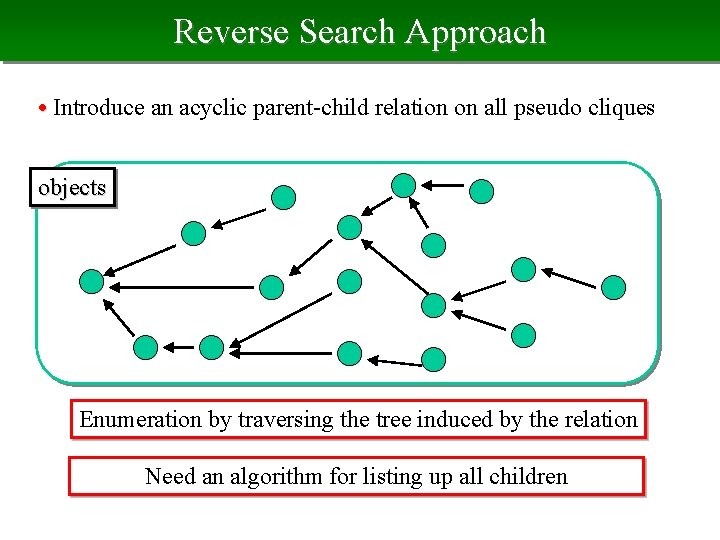
Reverse Search Approach • Introduce an acyclic parent-child relation on all pseudo cliques objects Enumeration by traversing the tree induced by the relation Need an algorithm for listing up all children

Parent of Pseudo Clique • v*(K) : min. deg. min. index vertex in G[K] • The parent of pseudo clique K K＼v*(K) The parent of K K • Density of K = ave. degree G[K] / (|K|-1) • The parent is the removal of most "sparse" vertex from K, thus is a pseudo clique • The parent is smaller than its child　 　acyclic relation

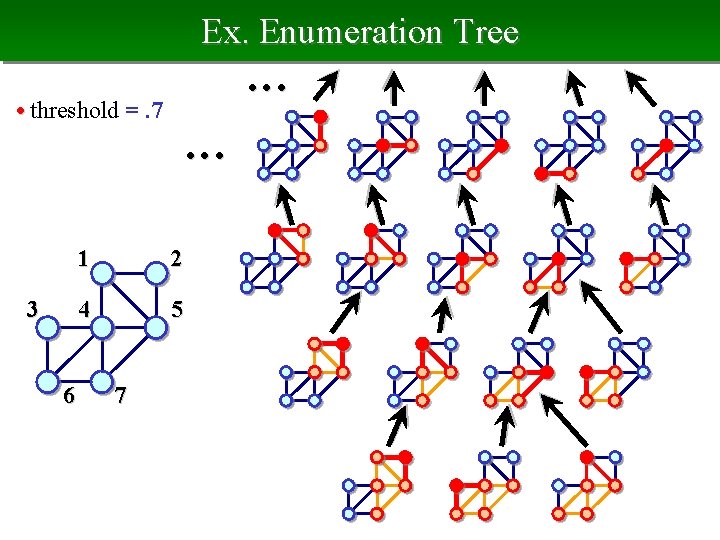
Ex. Enumeration Tree • • • • threshold =. 7 • • • 3 6 1 2 4 5 7

Finding Children • A child is obtained by adding a vertex to the parent • deg. K(v): #vertices in K adjacent to v (can be maintained in O(Δ) time for vertex addition) • K∪v is a child of K ① K∪v is a pseudo clique lower bound for deg. K(v) ② v*(K∪v) = v upper bound for deg. K(v) - deg. K(v) < min. deg. of K K∪v is always a child - deg. K(v) > min. deg. of K +1 K∪v never be a child • deg. K(v) ＝ min. deg. of K or +1 next slide…

Detailed Condition • S(K): sequence of vertices in K in the order of (degree, index) • v is a child v is the top of S(K∪v) top of S(K) is v*(K) • v is child only if v is adjacent to all vertices preceding to v in S(K) • For each vertex, find the first "non-adjacent vertex" in S(K) • This can be done in O(Δ 2) time Computation time for one iteration is O(Δ 2 + log |V|) ( O(Δk + log |V|) if k-degenerate)

Computational Experiments

Implementation • Code is a simple version - update |deg. K(vi)| at each addition adding u to K takes O(deg(u)) time - to find children, vi satisfying θ|K|(|K|+1) - (#edges in K) ≦ | deg. K(vi)| ≦ d*(K)+1 O( C d*(K)) = O(|E|) time + O(1) time for each C : = #vertices vi, | deg. K(vi)| = d*(K), d*(K)+1 Seems to be not large for #children

Problem Instances • Pentium M 1. 1 GHz, 256 MB memory, Cygwin, C, gcc • Test instances are: - random graphs (make edge with probability p), - locally dense random graphs (vertex i is adjacent to vertices from i-k to i+k with probability 1/2 - graphs generated from real-world data (co-author graph)

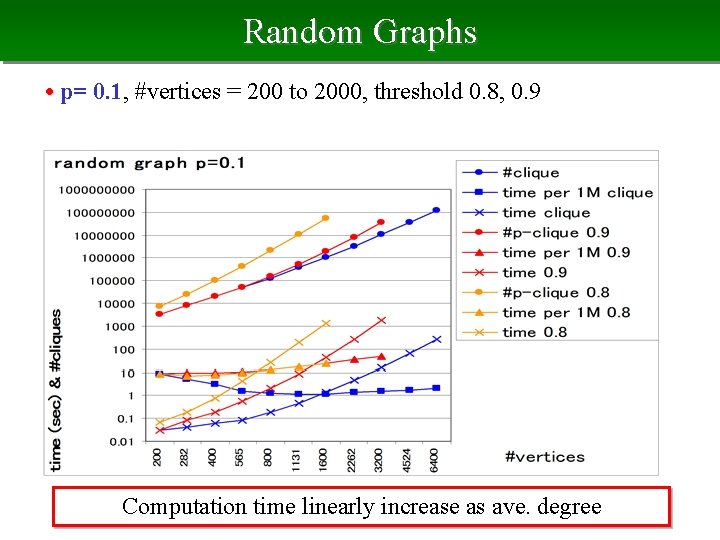
Random Graphs • p= 0. 1, #vertices = 200 to 2000, threshold 0. 8, 0. 9 Computation time linearly increase as ave. degree

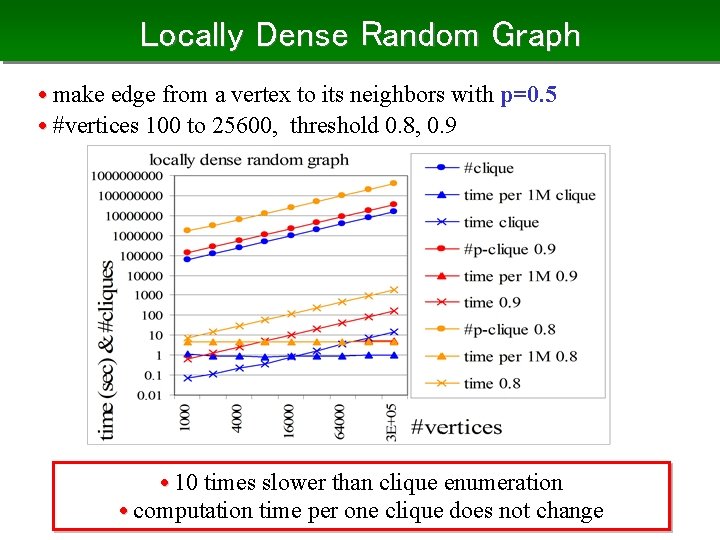
Locally Dense Random Graph • make edge from a vertex to its neighbors with p=0. 5 • #vertices 100 to 25600, threshold 0. 8, 0. 9 • 10 times slower than clique enumeration • computation time per one clique does not change

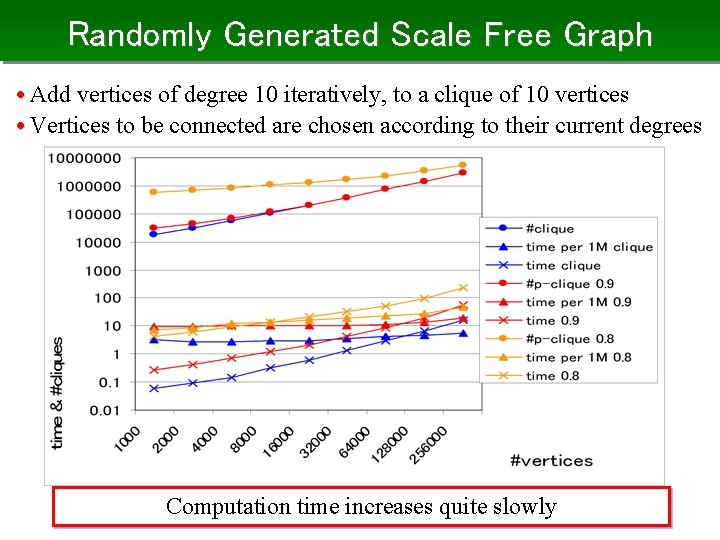
Randomly Generated Scale Free Graph • Add vertices of degree 10 iteratively, to a clique of 10 vertices • Vertices to be connected are chosen according to their current degrees Computation time increases quite slowly

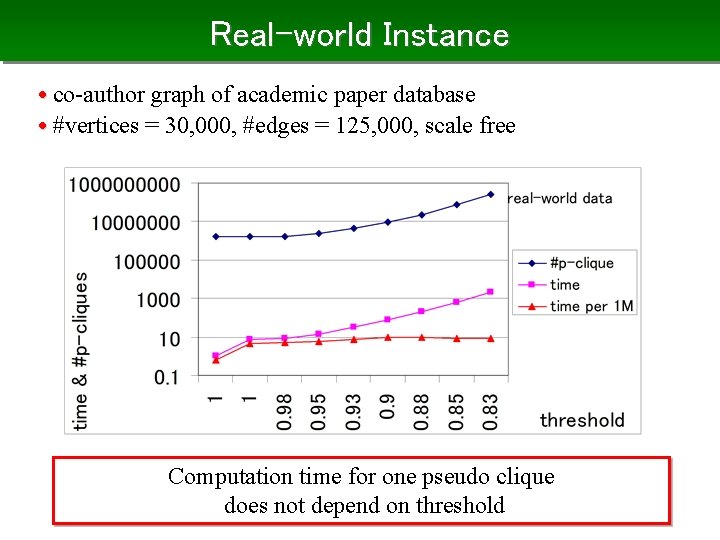
Real-world Instance • co-author graph of academic paper database • #vertices = 30, 000, #edges = 125, 000, scale free Computation time for one pseudo clique does not depend on threshold

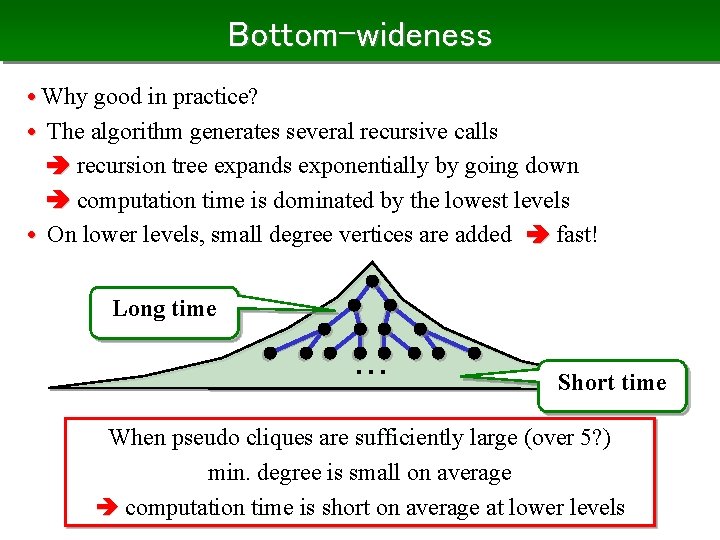
Bottom-wideness • Why good in practice? • The algorithm generates several recursive calls recursion tree expands exponentially by going down computation time is dominated by the lowest levels • On lower levels, small degree vertices are added fast! Long time ・・・ Short time When pseudo cliques are sufficiently large (over 5? ) min. degree is small on average computation time is short on average at lower levels

Conclusion • First polynomial delay polynomial space algorithm for enumerating pseudo cliques • Hardness result for straight forward branch-and-bound • Evaluate practical efficiency by computational experiments Future works: • Explain the gap between theory and practice • Introduce maximality and their enumeration • Apply the technique to other structures (pseudo bla bla) (path, tree, bipartite clique, matching …) • What is crucial for the compuation (enumeration) of structures with ambiguity