Neurophysics part 2 Adrian Negrean adrian negreancncr vu

Neurophysics - part 2 - Adrian Negrean adrian. negrean@cncr. vu. nl

Contents 1. Aim of this class 2. A first order approximation of neuronal biophysics 1. Introduction 2. Electro-chemical properties of neurons 3. Ion channels and the Action Potential 4. The Hodgkin-Huxley model 5. The Cable equation 6. Multi-compartmental models

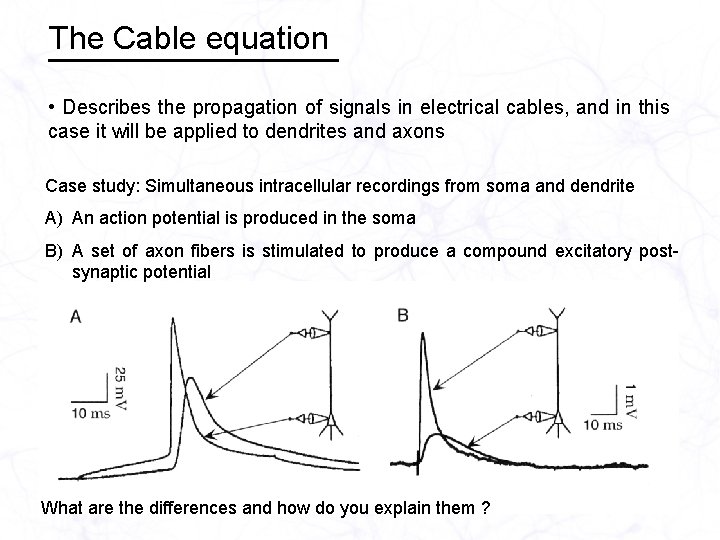
The Cable equation • Describes the propagation of signals in electrical cables, and in this case it will be applied to dendrites and axons Case study: Simultaneous intracellular recordings from soma and dendrite A) An action potential is produced in the soma B) A set of axon fibers is stimulated to produce a compound excitatory postsynaptic potential What are the differences and how do you explain them ?

• The longitudinal resistance of an axon or dendrite is: with r. L - intracellular resistivity ( m) Δx - segment length a - segment radius • The intracellular resistivity depends on the ionic composition of the intracellular milieu (and on the distribution of organelles)

• The longitudinal current through such a segment is: where ΔV(x, t) is the voltage gradient across the segment • Currents flowing in the increasing direction of x are defined to be positive

• In the limit : • Besides the longitudinal currents, there are several membrane currents flowing in/out of the segment: do you understand the formula ?

• Applying the principle of charge conservation for the previous cable segment we get: • Divide the above by such that the r. h. s. is in the limit

• Under the assumption that r. L does not vary with position the cable equation is obtained: • The radius of the cable is allowed to vary to simulate the tapering of dendrites • Boundary conditions required for V(x, t) and • Linear cable approximation: Ohmic membrane current im

• Use change of variables • And multiply by rm to get: with membrane time constant and electrotonic length (in the linear cable approximation)

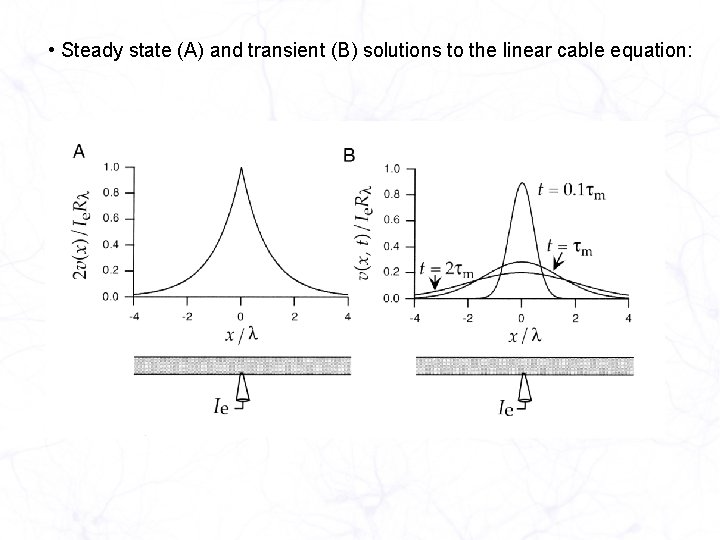
• Steady state (A) and transient (B) solutions to the linear cable equation:

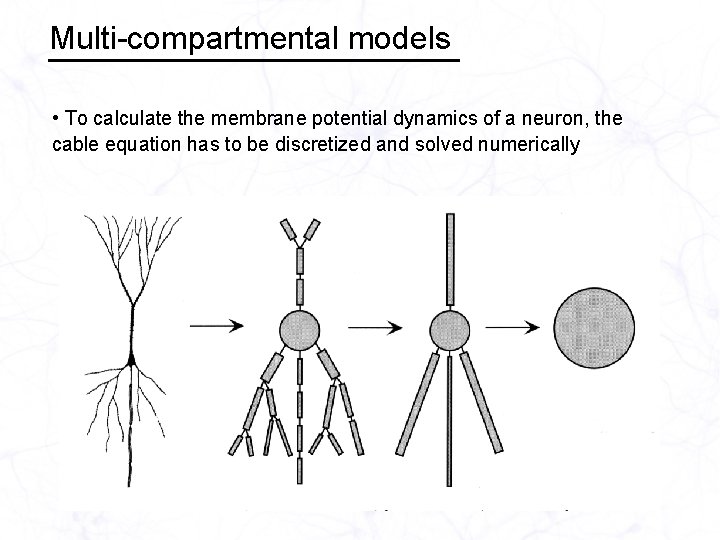
Multi-compartmental models • To calculate the membrane potential dynamics of a neuron, the cable equation has to be discretized and solved numerically

• The membrane potential dynamics of a single isolated compartment is described by: injected current through electrode specific membrane capacitance (Fm 2) surface area of compartment membrane currents due to ion-channels / membrane area • Several compartments coupled in a non-branching manner:

• The Ohmic coupling constants between two compartments with same length and radii:

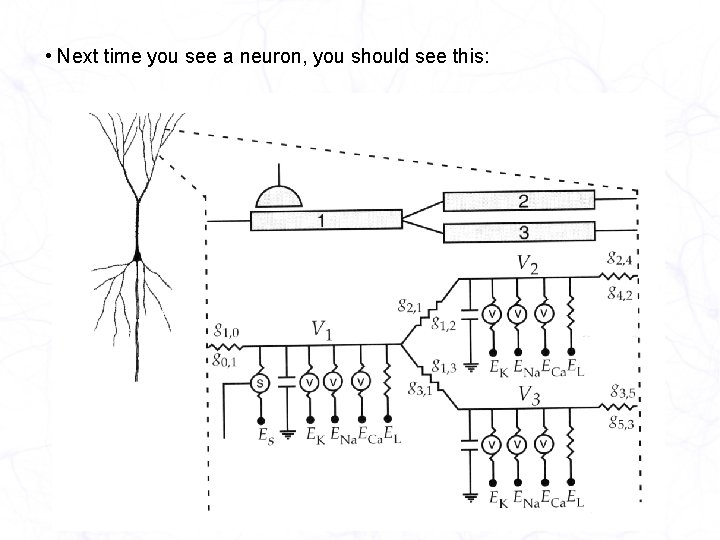
• Next time you see a neuron, you should see this: