Network Topology Singlelevel Diversity Coding System DCS An

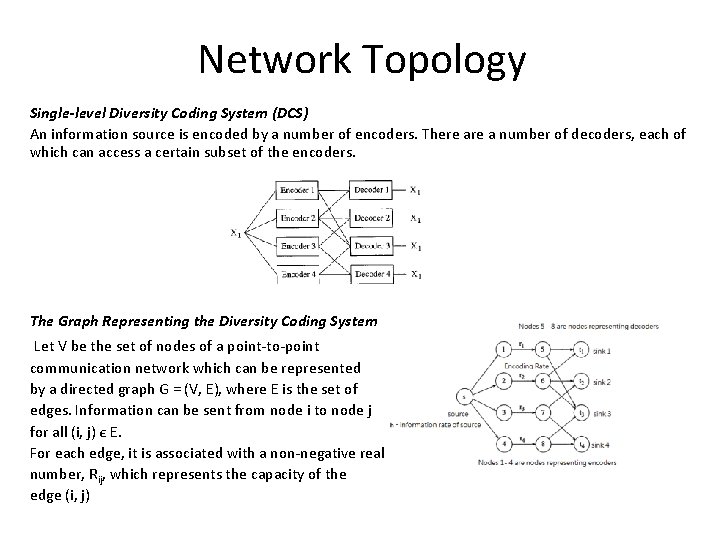
Network Topology Single-level Diversity Coding System (DCS) An information source is encoded by a number of encoders. There a number of decoders, each of which can access a certain subset of the encoders. The Graph Representing the Diversity Coding System Let V be the set of nodes of a point-to-point communication network which can be represented by a directed graph G = (V, E), where E is the set of edges. Information can be sent from node i to node j for all (i, j) є E. For each edge, it is associated with a non-negative real number, Rij, which represents the capacity of the edge (i, j)

To specify the multicast requirement, apart from defining the information rate, we let a: {1, …, m} -> V and b: {1, …, m} -> 2 V be the arbitrary mappings. For the single source problem, let a(1) = s, and b(1) = {t 1, …, t. L}. Also, R 15, R 26, R 37, R 48 correspond to r 1, r 2, r 3, and r 4 respectively. F = [Fij, (i, j) ϵ E]: flow in G from s to tl if for all (i, j) ϵ E 0 <= Fij <= Rij F is a max flow from source to sink and in order for a decoder to reconstruct the source successfully, the sum of coding rates of the encoders accessible by this decoder is at least h such that the value of max-flow from the source to the sink is referred to the capacity of the graph i. e. , r 1 + r 2 => h r 2 + r 3 => h r 1 + r 2 + r 4 => h r 3 + r 4 => h Since there is no constraint (in ideal) case on the coding rate in these edges, we interpret the capacity of each edge as infinity.

Introduction to Transfer Matrices M 1 = A(I – F)-1 BT, where I is the |E| x |E| identity matrix The determinant of the transfer matrix M 1 = A(I – F)-1 BβT for receiver β in a network code can be calculated as |M 1| = (-1)r(v + 1)|M 2| where M 2 corresponds to the Edmonds matrix with appropriately chosen coefficients. • • The coefficients {ai, j, fi, j, bβi, l ϵ Fq} can be collected into r x v matrices A = (ai, j) and Bβ = (bβi, j) and the v x v matrix F = (fl, j), whose structure is constrained by the network. For a multicast connection problem to be feasible, (i. e. , satisfies the max-flow min-cut theorem) the transfer matrix has non-zero determinant.

Delay-Free Networks (Multicast of Information) Let a delay-free communication network G and a solvable multicast network problem be given with one source and N receivers. Let R be the rate at which the source generates information. There exists a solution to the network coding problem in a finite field F 2^m (q = 2^m) Proof: Each entry in the matrix (I – F)-1 has degree at most one in any variable. Hence the degree of each variable in the determinant of a particular transfer matrix is at most R. It follows that the relevant polynomial has degree at most NR in any variable. However, the upper bound can still be tightened when there exists a solution in a finite field Fq where q > N for a feasible multicast connection problem with N receivers. Proof: Since no variable coefficients appear in more than one entry of the Edmonds matrix, no product term in the determinant polynomial contains a variable coefficients raised to an exponent greater than 1. Thus, the largest exponent of any variable in a product of d such determinants is at most d.

How to solve network jamming (1) If network coding is allowed, then 4 bits can be multicast to all the sinks if 2 bits are sent in each edge. If network coding is not allowed, only 3 bits can be multicast to all sinks. Let B = {b 1, …, bk} be the set of bits to be multicast to all the sinks. Let the set of bits sent in the edge (s, i) be Bi, where |Bi| = 2, i = 1, 2, 3. Since two bits are sent in each edge in the network and network coding is allowed, B 3 ∪ (B 1 ∩ B 2) = (B 3 ∪ B 1) ∩ (B 3 ∪ B 2) = B Therefore, K = | B 3 ∪ (B 1 ∩ B 2)| <= | B 3| + |B 1 ∩ B 2| = | B 3| + | B 1| + | B 2| - |B 1 ∪ B 2| = 6 – K which indicates that k <= 3. The throughput of the network can be increased by onethird in this case.

How to solve network jamming (2) We can increase the probabilities of success of randomized routing scheme RR and randomized coding scheme RC. Transmission to a particular receiver is successful if the receiver gets two different processes instead of duplicates of the same process. Consider the rectangular grid network: • • RR Scheme: The source node sends one process in both directions on one axis and the other process in both directions along the other axis A node receiving information on one link sends the same information on its three other links A node receiving signals on two links sends one of the incoming signals on one of its two other links with equal probability, and the other signal on the remaining link. RC Scheme: The first two steps are exactly the same as the RR Scheme except for the last step: A node receiving signals on two links sends a random linear combination of the source signals on each of its two other links.

How to solve network jamming (2) (cont’) Let A and B be the events: receiver located at grid position (x, y) relative to the source receives both source processes & a receiver located at grid position (x, y) relative to the source can decode both processes respectively. For Random Routing Scheme RR: For Random Coding Scheme RC: Without using these two schemes, the prob. of successes are usually lower. That means more retransmission may be required. Moreover, in the RC scheme, the increase in field size will increase the prob. of successes.