Mt Rushmore South Dakota 3 9 Derivatives of

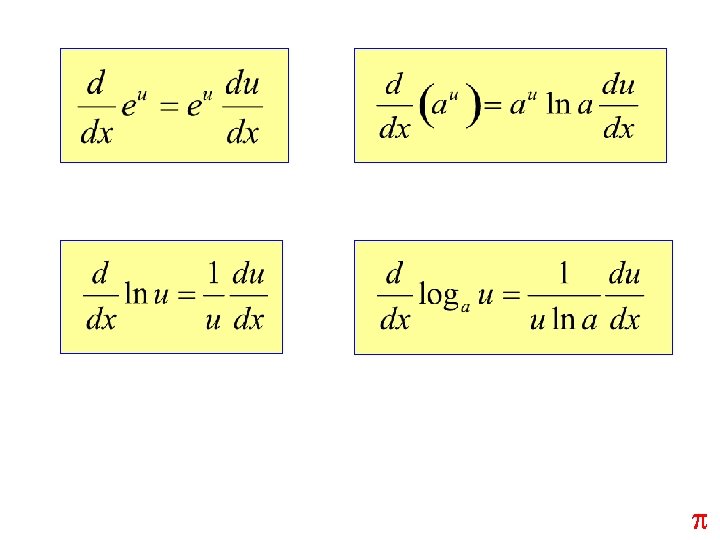
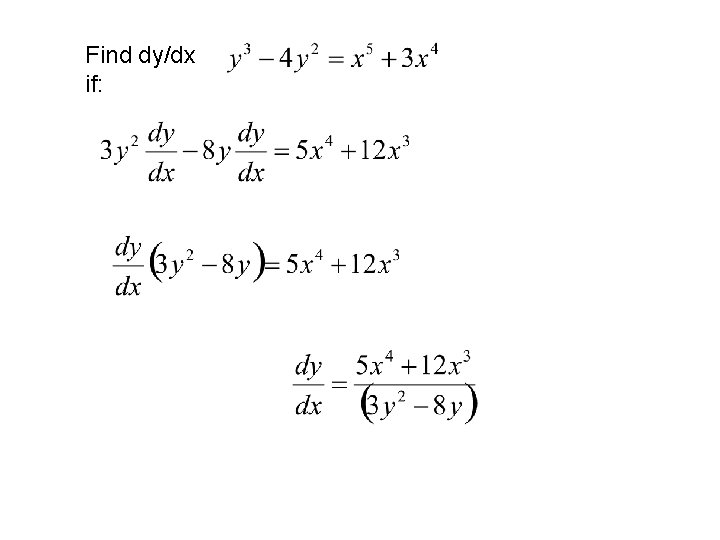
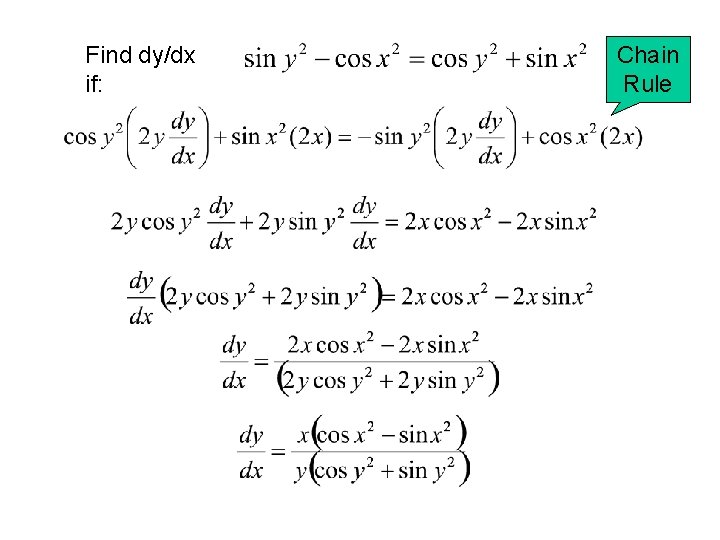
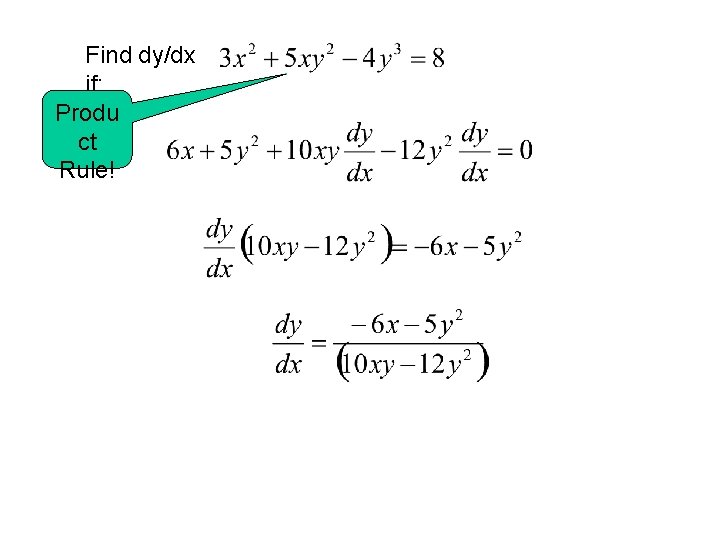
  • Slides: 22
Download presentation
Mt. Rushmore, South Dakota 3. 9: Derivatives of Exponential and Logarithmic Functions Photo by

Mt. Rushmore, South Dakota 3. 9: Derivatives of Exponential and Logarithmic Functions Photo by Vickie Kelly, 2007 Greg Kelly, Hanford High School, Richland, Washington

Look at the graph of The slope at x=0 appears to be 1. If

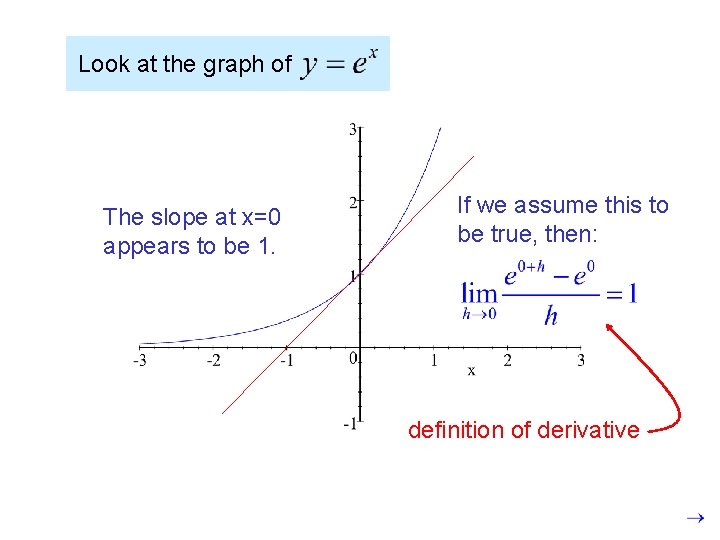
Look at the graph of The slope at x=0 appears to be 1. If we assume this to be true, then: definition of derivative

Now we attempt to find a general formula for the derivative of using the

Now we attempt to find a general formula for the derivative of using the definition. This is the slope at x=0, which we have assumed to be 1.

is its own derivative! If we incorporate the chain rule: We can now use

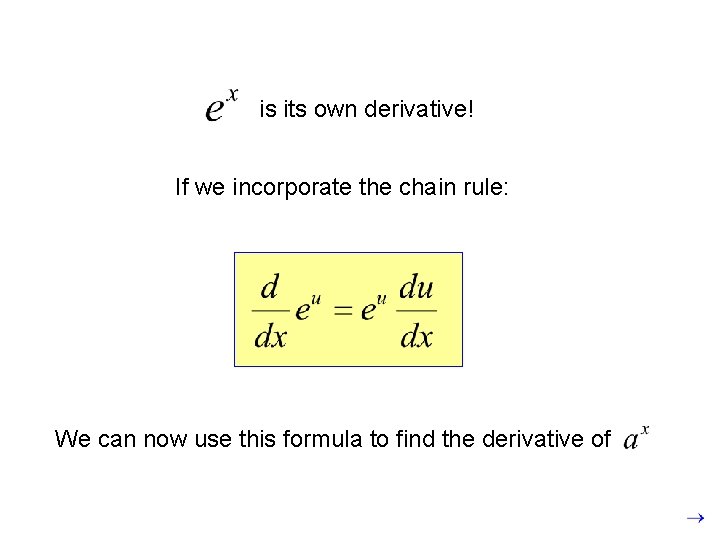
is its own derivative! If we incorporate the chain rule: We can now use this formula to find the derivative of

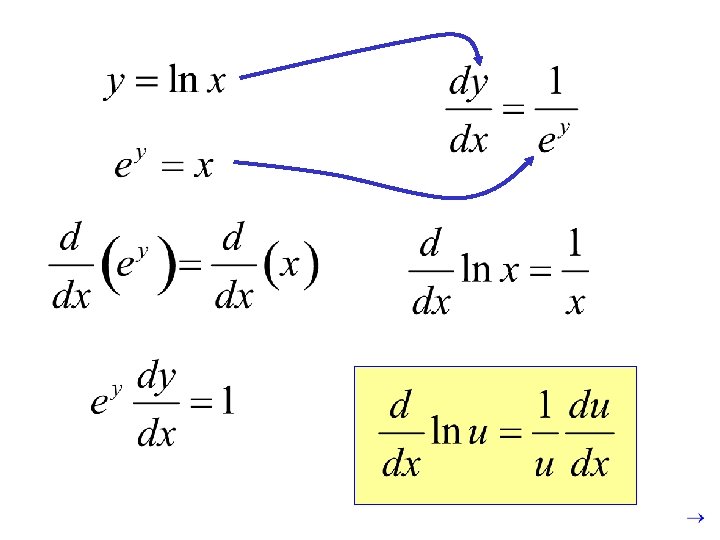
( and are inverse functions. ) (chain rule)

( and are inverse functions. ) (chain rule)

( is a constant. ) Incorporating the chain rule:

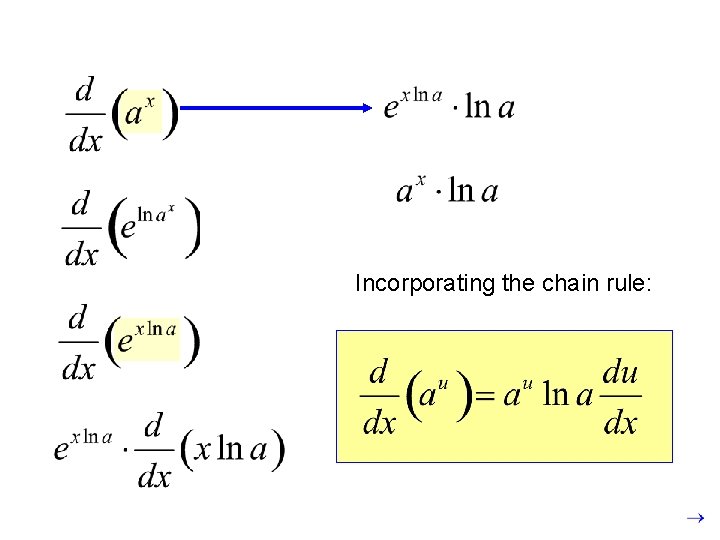
( is a constant. ) Incorporating the chain rule:

So far today we have: Now it is relatively easy to find the derivative

So far today we have: Now it is relatively easy to find the derivative of .

To find the derivative of a common log function, you could just use the

To find the derivative of a common log function, you could just use the change of base rule for logs: The formula for the derivative of a log of any base other than e is:

p

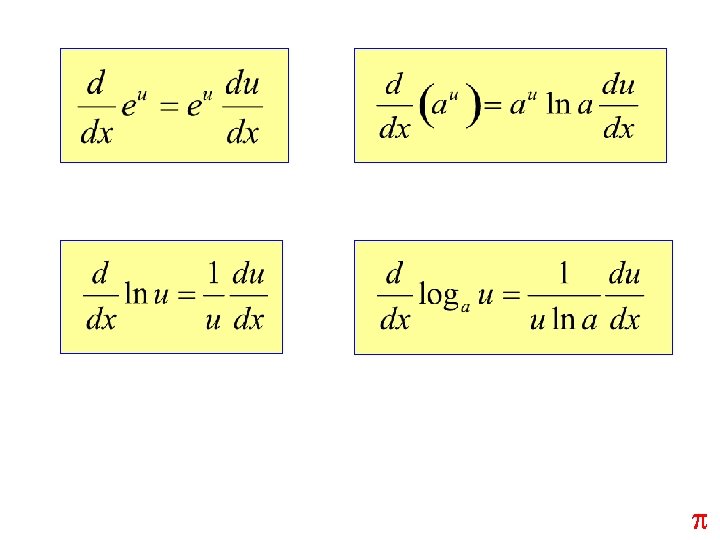
p

Implicit Differentiation 3. 6

Implicit Differentiation 3. 6

Implicit Differentiation So far, all the equations and functions we looked at were all

Implicit Differentiation So far, all the equations and functions we looked at were all stated explicitly in terms of one variable: In this function, y is defined explicitly in terms of x. If we re-wrote it as xy = 1, y is now defined implicitly in terms of x. It is easy to find the derivative of an explicit function, but what about:

This is not a function, but it would still be nice to be able

This is not a function, but it would still be nice to be able to find the slope. Do the same thing to both sides. Note use of chain rule.

This can’t be solved for y. This technique is called implicit differentiation. 1 Differentiate

This can’t be solved for y. This technique is called implicit differentiation. 1 Differentiate both sides w. r. t. x. 2 Solve for .

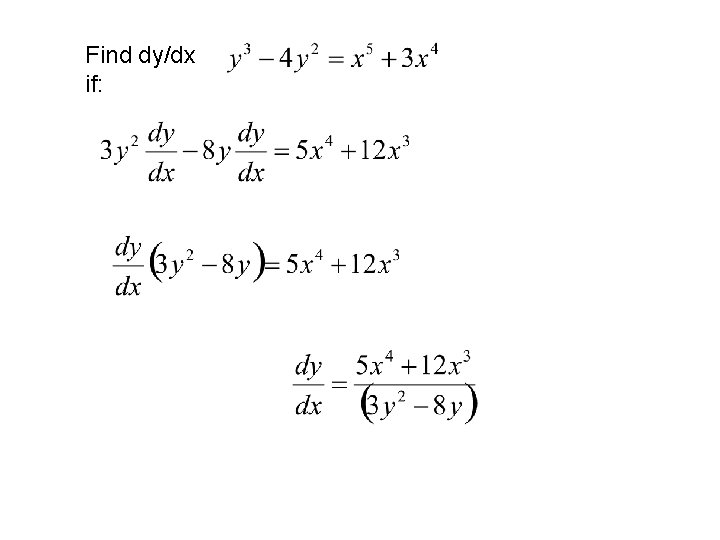
Find dy/dx if:

Find dy/dx if:

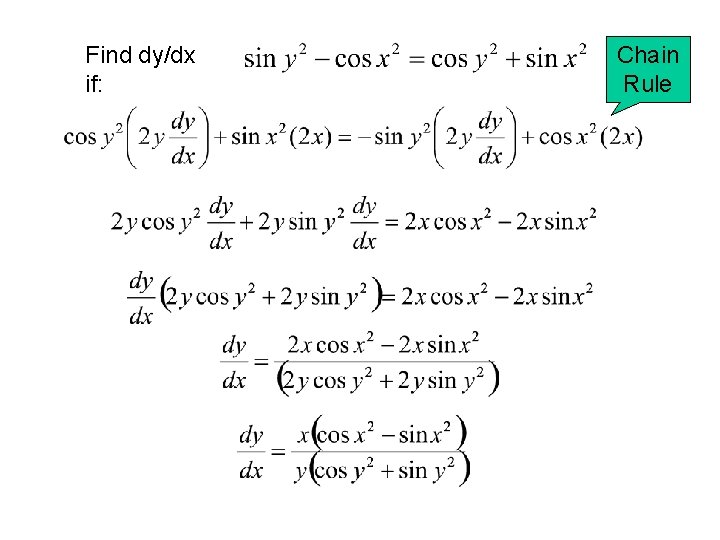
Find dy/dx if: Chain Rule

Find dy/dx if: Chain Rule

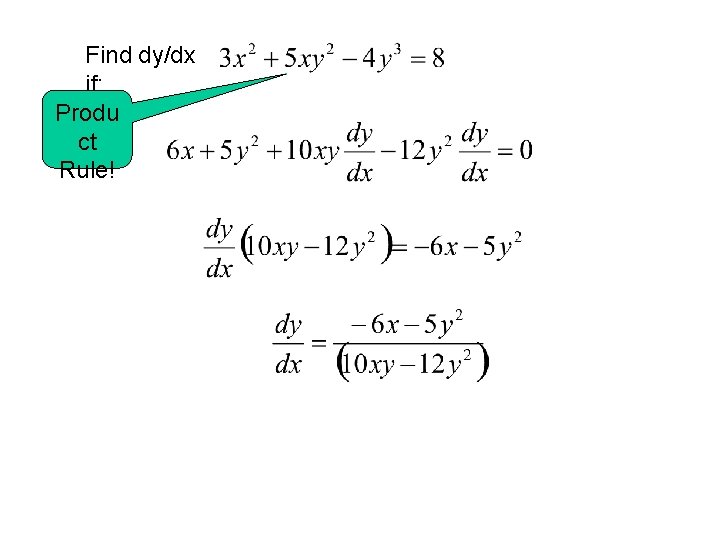
Find dy/dx if: Produ ct Rule!

Find dy/dx if: Produ ct Rule!

Find the equations of the lines tangent and normal to the curve at .

Find the equations of the lines tangent and normal to the curve at . We need the slope. Since we can’t solve for y, we use implicit differentiation to solve for Note product rule. .

Find the equations of the lines tangent and normal to the curve at tangent:

Find the equations of the lines tangent and normal to the curve at tangent: . normal: Normal line is perpendic ular to tangent

Product Rule is easier than quotient rule, so let’s cross multiply! Find derivative at

Product Rule is easier than quotient rule, so let’s cross multiply! Find derivative at (1, 1)

Higher Order Derivatives Find if . Substitute back into the equation.

Higher Order Derivatives Find if . Substitute back into the equation.

JRVR South Dakota State South Dakota South DakotaJRVR South Dakota State South Dakota South Dakota
Mt Rushmore South Dakota Derivatives of Exponential andMt Rushmore South Dakota Derivatives of Exponential and
Mount Rushmore Mount Rushmore National Memorial without aMount Rushmore Mount Rushmore National Memorial without a
RUSHMORE CONNECTOR TRAIL WELCOME Rushmore Connector Trail EnvironmentalRUSHMORE CONNECTOR TRAIL WELCOME Rushmore Connector Trail Environmental
Rushmore Einfhrung oder wie Sie Fehler vermeiden RushmoreRushmore Einfhrung oder wie Sie Fehler vermeiden Rushmore
Mount Rushmore Mount Rushmore one of the mostMount Rushmore Mount Rushmore one of the most
Washington Jefferson Roosevelt Lincoln Mount Rushmore Mount RushmoreWashington Jefferson Roosevelt Lincoln Mount Rushmore Mount Rushmore
South Dakota By Brian Mc Court Mount RushmoreSouth Dakota By Brian Mc Court Mount Rushmore
Unfinished Business Mount Rushmore in South Dakota isUnfinished Business Mount Rushmore in South Dakota is
REGIONAL SNAPSHOT Northwest South Dakota Region South DakotaREGIONAL SNAPSHOT Northwest South Dakota Region South Dakota
REGIONAL SNAPSHOT Northwest South Dakota Region South DakotaREGIONAL SNAPSHOT Northwest South Dakota Region South Dakota
South Dakota Science Assessment SDSA South Dakota ScienceSouth Dakota Science Assessment SDSA South Dakota Science
SOUTH DAKOTA DEPARTMENT OF REVENUE South Dakota AssociationSOUTH DAKOTA DEPARTMENT OF REVENUE South Dakota Association
SOUTH DAKOTA Gitsba Hamida III IR South DakotaSOUTH DAKOTA Gitsba Hamida III IR South Dakota
Midwest Unit Foods 2 North Dakota South DakotaMidwest Unit Foods 2 North Dakota South Dakota
Midwest North Dakota South Dakota Nebraska Kansas OklahomaMidwest North Dakota South Dakota Nebraska Kansas Oklahoma
Module Derivatives and Related Accounting Issues Derivatives DerivativesModule Derivatives and Related Accounting Issues Derivatives Derivatives
CREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivativesCREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivatives
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
Derivatives and Gradients Derivatives Derivatives tell us whichDerivatives and Gradients Derivatives Derivatives tell us which
3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric