Movimiento Circular Acelerado La velocidad angular El movimiento

Movimiento Circular Acelerado α

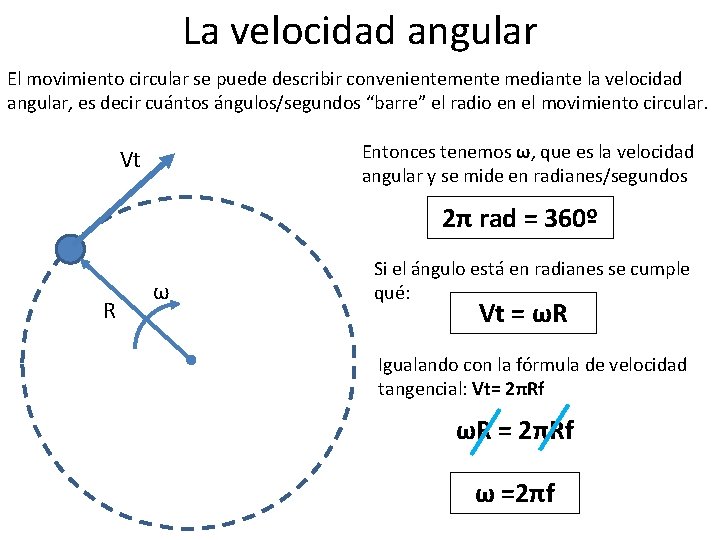
La velocidad angular El movimiento circular se puede describir convenientemente mediante la velocidad angular, es decir cuántos ángulos/segundos “barre” el radio en el movimiento circular. Entonces tenemos ω, que es la velocidad angular y se mide en radianes/segundos Vt 2π rad = 360º R ω Si el ángulo está en radianes se cumple qué: Vt = ωR Igualando con la fórmula de velocidad tangencial: Vt= 2πRf ωR = 2πRf ω =2πf

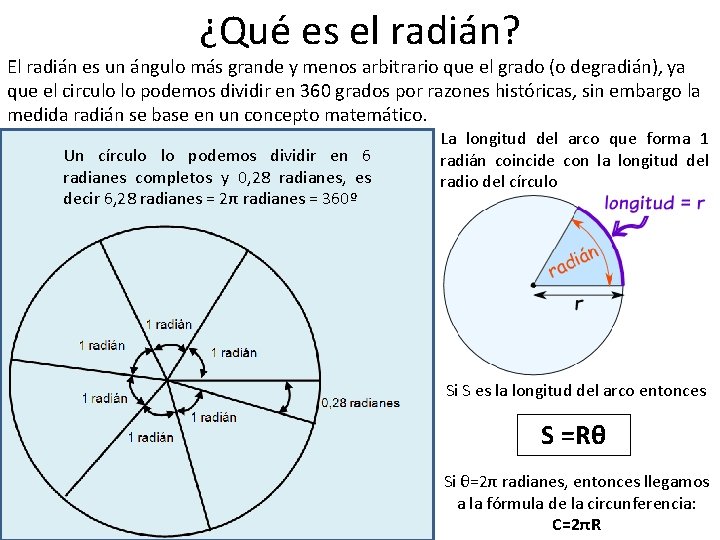
¿Qué es el radián? El radián es un ángulo más grande y menos arbitrario que el grado (o degradián), ya que el circulo lo podemos dividir en 360 grados por razones históricas, sin embargo la medida radián se base en un concepto matemático. Un círculo lo podemos dividir en 6 radianes completos y 0, 28 radianes, es decir 6, 28 radianes = 2π radianes = 360º La longitud del arco que forma 1 radián coincide con la longitud del radio del círculo Si S es la longitud del arco entonces S =Rθ Si θ=2π radianes, entonces llegamos a la fórmula de la circunferencia: C=2πR

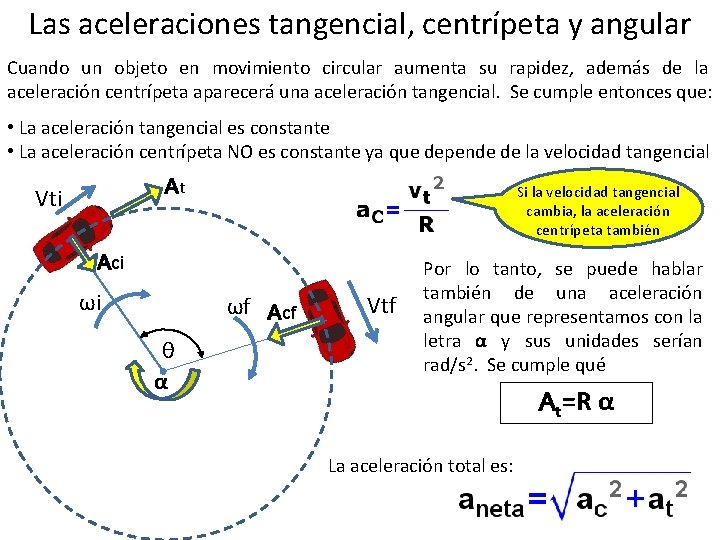
Las aceleraciones tangencial, centrípeta y angular Cuando un objeto en movimiento circular aumenta su rapidez, además de la aceleración centrípeta aparecerá una aceleración tangencial. Se cumple entonces que: • La aceleración tangencial es constante • La aceleración centrípeta NO es constante ya que depende de la velocidad tangencial At Vti Si la velocidad tangencial cambia, la aceleración centrípeta también Aci ωi ωf Acf θ α Vtf Por lo tanto, se puede hablar también de una aceleración angular que representamos con la letra α y sus unidades serían rad/s 2. Se cumple qué At=R α La aceleración total es:

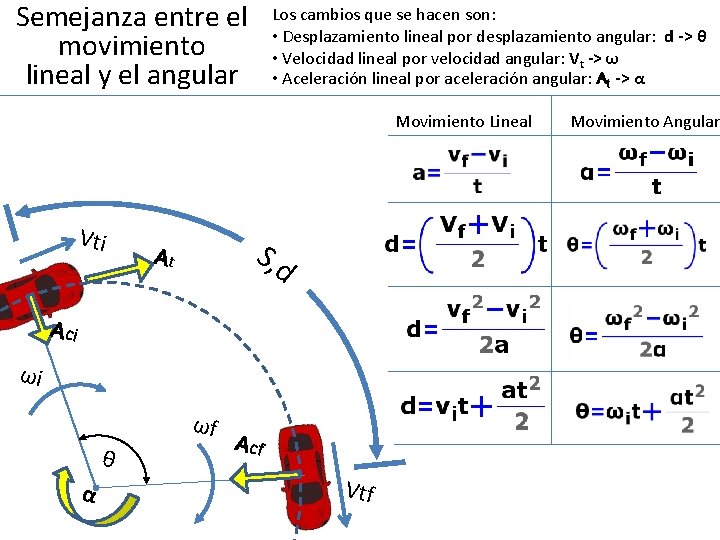
Semejanza entre el movimiento lineal y el angular Los cambios que se hacen son: • Desplazamiento lineal por desplazamiento angular: d -> θ • Velocidad lineal por velocidad angular: Vt -> ω • Aceleración lineal por aceleración angular: At -> α Movimiento Lineal Vti S, d At A ci ωi ωf θ α Acf Vtf Movimiento Angular

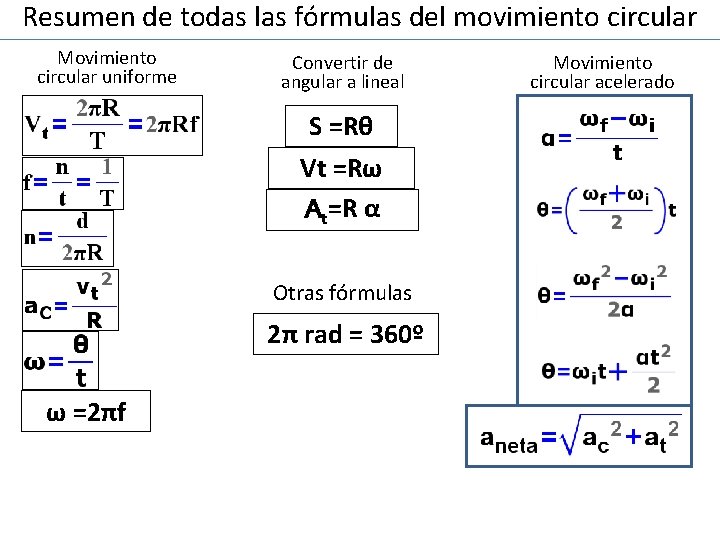
Resumen de todas las fórmulas del movimiento circular Movimiento circular uniforme Convertir de angular a lineal S =Rθ Vt =Rω At=R α Otras fórmulas 2π rad = 360º ω =2πf Movimiento circular acelerado

Ejercicio #1 ¿Cuál es el valor de la velocidad angular de una rueda que gira desplazándose 15 radianes en 0. 2 segundos? R/ • • Datos ω=¿ θ = 15 rad t = 0. 2 seg Fórmula =θ t Sustitución = 15 rad 0. 2 seg = 75 rad/seg.

Ejercicio #2 Determinar el valor de la velocidad angular y la frecuencia de una piedra atada a un hilo, si gira con un periodo de 0. 5 segundos. R/ • Datos Fórmula • ω=? =2π • f=? T • T = 0. 5 seg Sustitución • = 2 x 3. 14 = 12. 56 rad/seg. 0. 5 seg • f = 1/T => f = 1/ 0. 5 seg =2 ciclos/seg o 2 Hz.

Ejercicio #3 Hallar la velocidad angular y el periodo de una rueda que gira con una frecuencia de 430 revoluciones por minuto. R/ • Datos Fórmulas • ω=? =2πf • T=? T = 1/f • f = 430 rpm Sustitución y resultado: • 430 rpm x 1 min = 7. 17 rev/seg 60 seg • = 2 x 3. 14 x 7. 17 rev/seg = 45 rad/seg. • T = 1/7. 17 rev/seg = 0. 139 seg/rev.

Ejercicio #4 Encontrar la velocidad angular de un disco de 45 rpm, así como su desplazamiento angular, si su movimiento duró 3 minutos. R/ • Datos ω=? Fórmulas =2πf θ=? θ=ωt f = 45 rpm t = 3 min = 180 seg 45 rpm x 1 min = 0. 75 rev/seg 60 seg = 2 x 3. 14 x 0. 75 rev/seg = 4. 71 rad/seg. θ = 4. 71 rad/seg x 180 seg=847. 8 rad.

Ejercicio #5 Un engrane originalmente en reposo comenzó a girar y adquirió una velocidad de 2512 rad / s en 1. 5 s. ¿Cuál fue la aceleración angular? R/ • Datos ωf = 2512 rad / s ωi = 0 t = 1. 5 seg α= ? formula α = (ωf - ωi)/ t • Sustitución y resultado: α = 2512 rad/s = 1674. 66 rad/s 2. 1. 5 seg

Ejercicio #6 Un mezclador eléctrico incremento su velocidad angular de 20 rad / s a 120 rad / s en 0. 5 s. calcular: a) ¿Cuál fue el valor de su aceleración media? B) cual fue el valor de su desplazamiento angular en ese tiempo? R/ • Datos formula • ωi = 20 rad/ s α = ωf –ωi • ωf = 120 rad/ s t • t = 0. 5 s • a) α = ? θ = ωit + ⅟ 2α t 2 • b) θ = ? Sustitución y resultado: • α = 120 rad/ s – 20 rad/ s = 200 rad / s 2. • 0. 5 s • θ = 20 rad/ s x 0. 5 + (⅟ 2)200 rad/ s 2 (0. 5 seg)2. • = 10 rad/ s + 25 rad θ = 35 radianes.

Ejercicio #7 Determinar la velocidad angular final de una rueda a los 0. 1 minutos si se tenia una velocidad angular inicial de 6 rad/ s y sufre una aceleración angular de 5 rad/ s 2. R/ Datos formula • ωf =? ωf = ωi + αt • t = 0. 1 min = 6 s • ωi = 6 rad / s • α = 5 rad/ s 2. • Sustitución y resultado. • ωf = 6 rad/ s + (5 rad/ s 2 x 6 s) = 36 rad/ s.

Ejercicio #8 Una rueda que gira a 4 rev/ s aumenta su frecuencia a 20 rev/ s en 2 segundos. Determinar el valor de su aceleración angular. R/ • Datos formulas • fi = 4 rev/ s ω i = 2 π fi ff = 20 rev/ s ωf = 2 π ff • α =? • t=2 s • Sustitución y resultado: • ωi = 2 x 3. 14 x 4 rev/s= 25. 12 rad/s • ωf = 2 x 3. 14 x 20 rev/s = 125. 6 rad/ s • • • α = ωf - ωi t α = 125. 6 rad/ s – 25. 12 rad/ s 2 s α = 50. 24 rad / s 2.

Ejercicio #9 Una rueda gira con una velocidad angular inicial cuyo valor es de 18. 8 rad/seg experimentando una aceleración angular de 4 rad/seg 2 que dura 7 segundos. Calcular: a) ¿Qué valor de desplazamiento angular tiene a los 7 segundos? b) ¿Qué valor de velocidad angular lleva a los 7 segundos? R/ • Datos Fórmula • ωo = 18. 8 rad/seg a) θ = ωit + αt 2 • t = 7 seg • α = 4 rad /seg 2. b) ωf = ωi + αt • θ=? • ωf = ? Sustitución y resultado: θ = 18. 8 rad/seg x 7 seg + (4 rad/seg 2) (7 seg)2 2 • θ = 131. 6 rad + 98 rad = 229. 6 rad. • ωf = 18. 8 rad/seg + 4 rad/seg 2 x 7 seg • ωf = 18. 8 rad/seg + 28 rad/seg = 46. 8 rad/seg.