FSICA CINEMTICA MOVIMENTO UNIFORME MOVIMENTO VARIADO E CIRCULAR

FÍSICA: CINEMÁTICA, MOVIMENTO UNIFORME, MOVIMENTO VARIADO E CIRCULAR UNIFORME

MOVIMENTO RETILINEO UNIFORME (MRU) n Movimento – Se tem movimento tem velocidade. n Retilíneo – Linha Reta n Uniforme – Velocidade Constante 2

MU Características do MRU: Velocidade Constante n MOVIMENTO DA VACA Aceleração = 0 V = Velocidade escalar S = Deslocamento escalar t = Tempo gasto 3

MU n ΔS = Variação de espaço (metro – m) n ΔT = Variação de tempo (segundos – s) n V = Velocidade (metros por segundos – m/s) 4

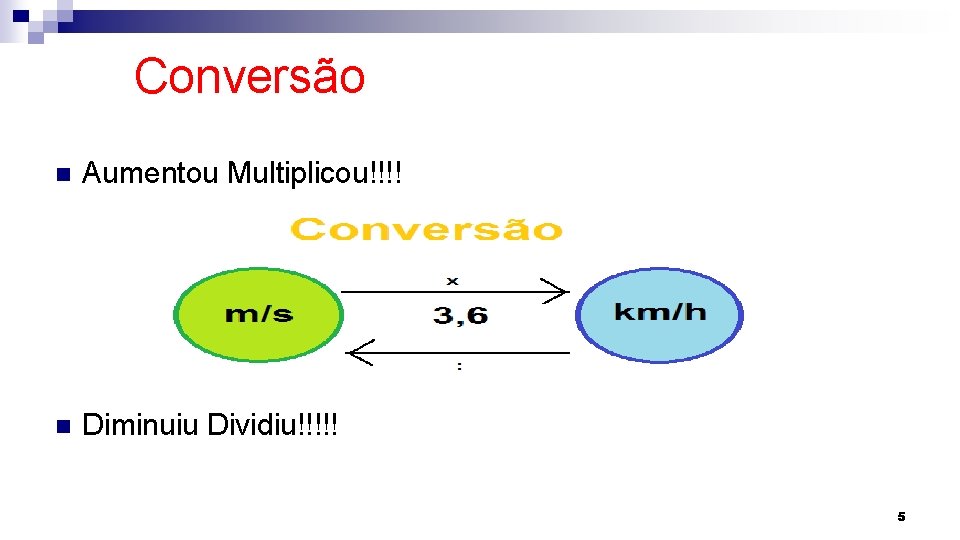
Conversão n Aumentou Multiplicou!!!! n Diminuiu Dividiu!!!!! 5

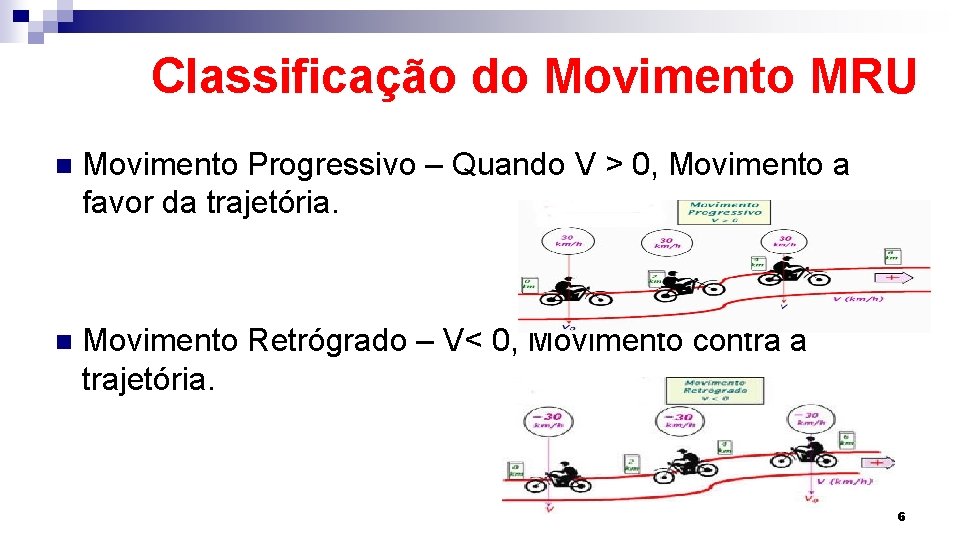
Classificação do Movimento MRU n Movimento Progressivo – Quando V > 0, Movimento a favor da trajetória. n Movimento Retrógrado – V< 0, Movimento contra a trajetória. 6

EQUAÇÕES DO MRU n Para calcular o deslocamento escalar do móvel: n Função horária dos espaços: 7

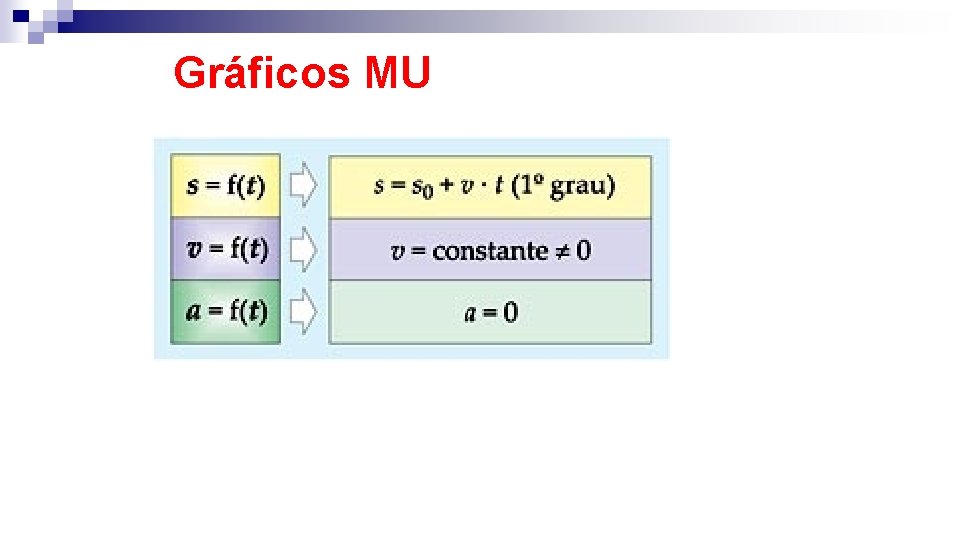
Gráficos MU

DIAGRAMAS HORÁRIOS DO MRU E MRUV

Analisando os Gráficos MU n Gráfico da Velocidade em função do Tempo (V x T) 10

Gráfico da Velocidade em função do Tempo (V x T) 11

Gráfico do Espaço em Função do Tempo (S x T) n Analisando a Equação: 12

Exercícios Modelos ENEM 1 - A tabela fornece, em vários instantes, a posição s de um automóvel em relação ao km zero da estrada em que se movimenta. A função horária que nos fornece a posição do automóvel, com as unidades fornecidas, é: a) s = 200 + 30 t b) s = 200 - 30 t c) s = 200 + 15 t d) s = 200 - 15 t e) s = 200 - 15 t 2 13

Movimento Retilíneo Uniformemente Variado (MRUV) n n n Surge a aceleração, que é do tipo constante Pode ser acelerado ou desacelerado Velocidade varia sempre da mesma forma. a= Onde: V é a velocidade final ( m/s) V 0 é a velocidade inicial ( m/s ) T é o instante final ( s) T 0 é o instante inicial (s ) a é aceleração escalar média (m/s 2 ) n 14

Classificação dos Movimentos MRUV O movimento pode ser acelerado ou desacelerado. Acelerado: O valor da velocidade aumenta ao longo da trajetória. V>0 ea>0 OU V < 0 e a < 0 Desacelerado: O módulo da velocidade diminui ao longo do tempo. V>0 ea<0 OU V < 0 e a > 0 15

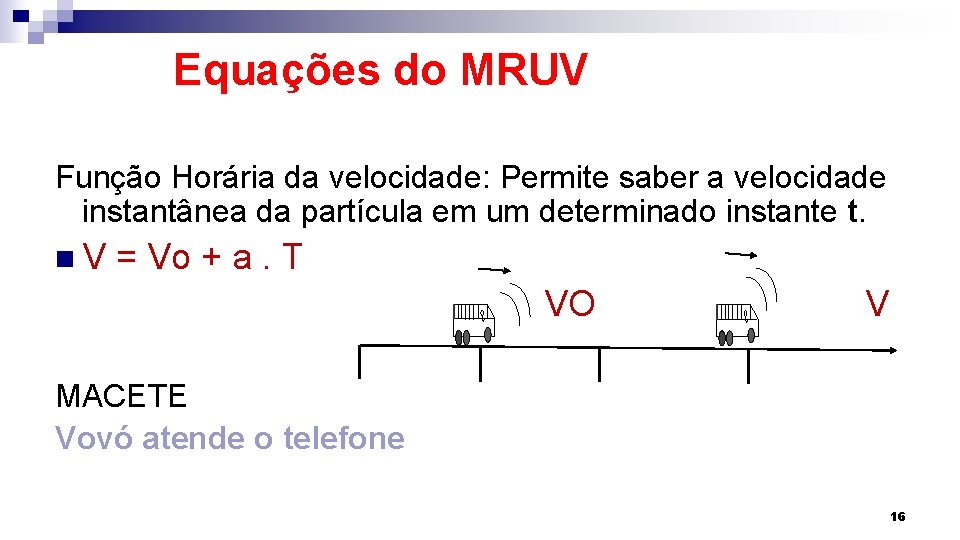
Equações do MRUV Função Horária da velocidade: Permite saber a velocidade instantânea da partícula em um determinado instante t. n V = Vo + a. T VO V MACETE Vovó atende o telefone 16

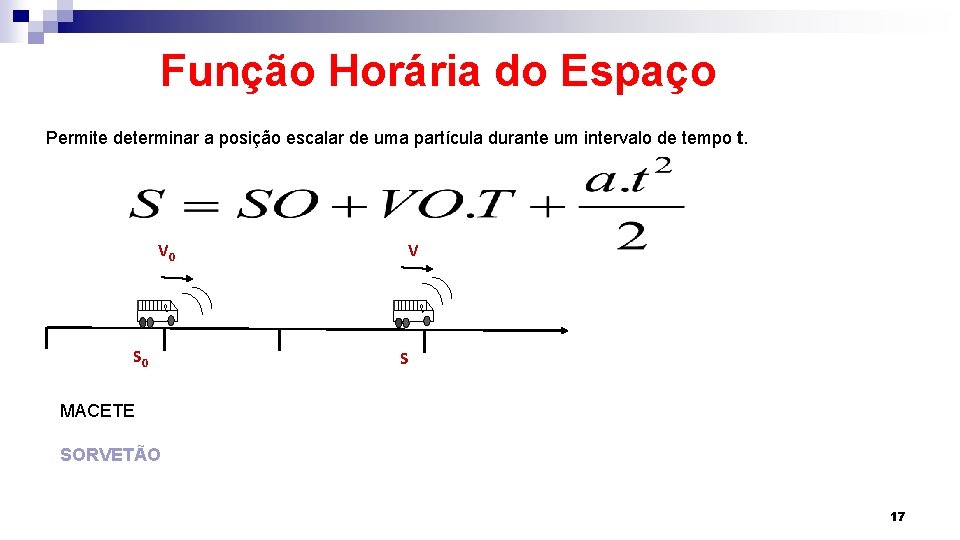
Função Horária do Espaço Permite determinar a posição escalar de uma partícula durante um intervalo de tempo t. V 0 S 0 V S MACETE SORVETÃO 17

Equação de Torricelli

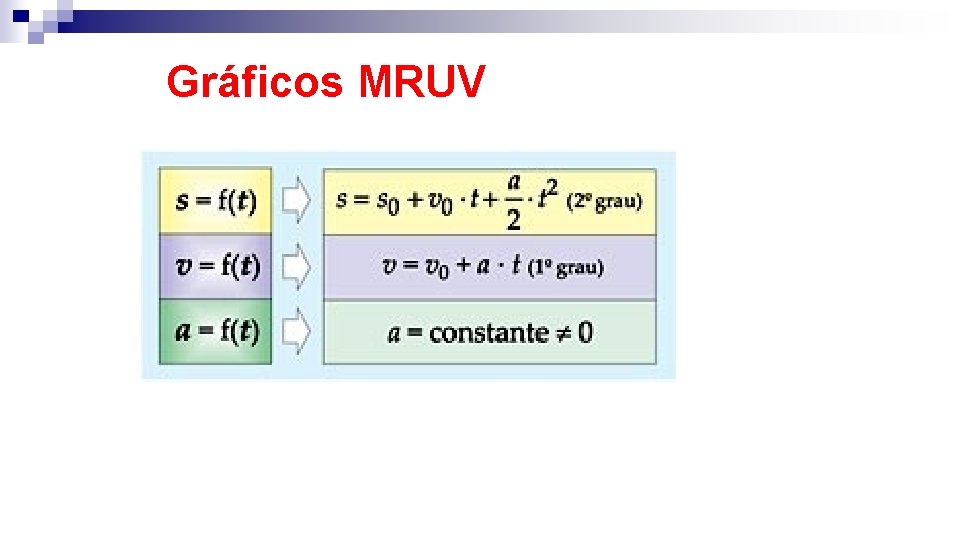
Gráficos MRUV

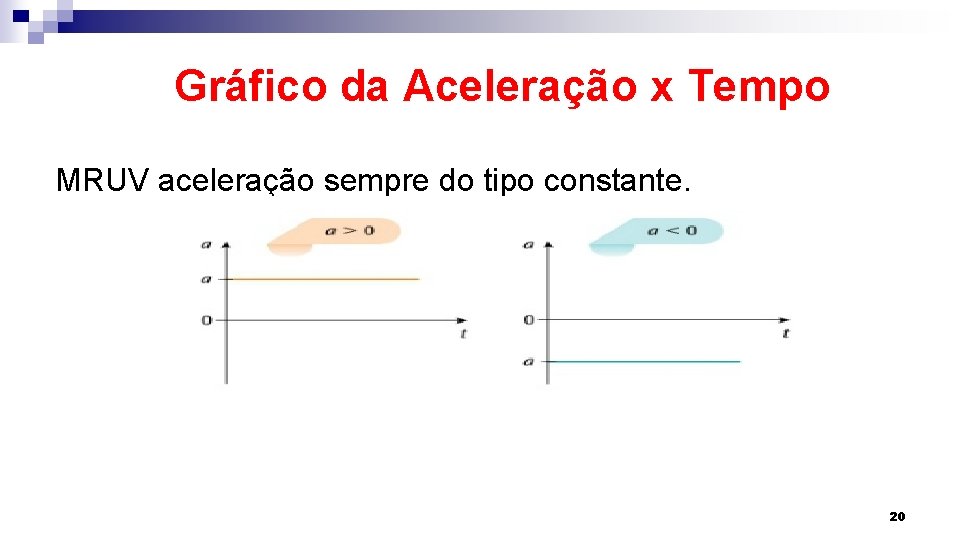
Gráfico da Aceleração x Tempo MRUV aceleração sempre do tipo constante. 20

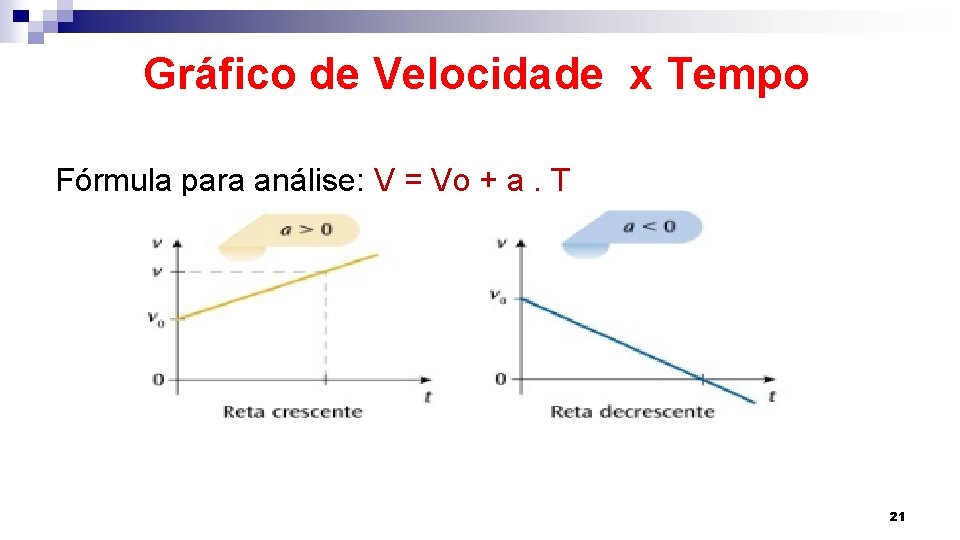
Gráfico de Velocidade x Tempo Fórmula para análise: V = Vo + a. T 21

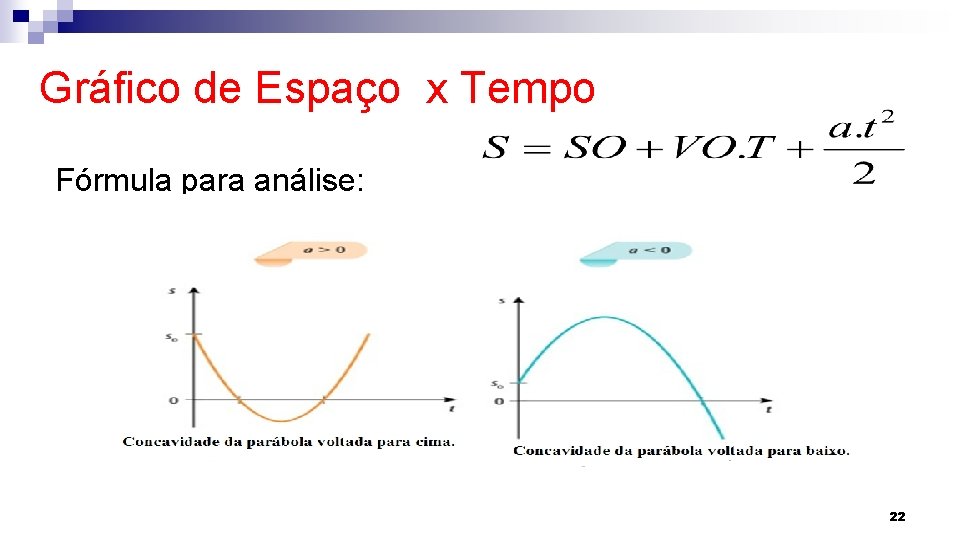
Gráfico de Espaço x Tempo Fórmula para análise: 22

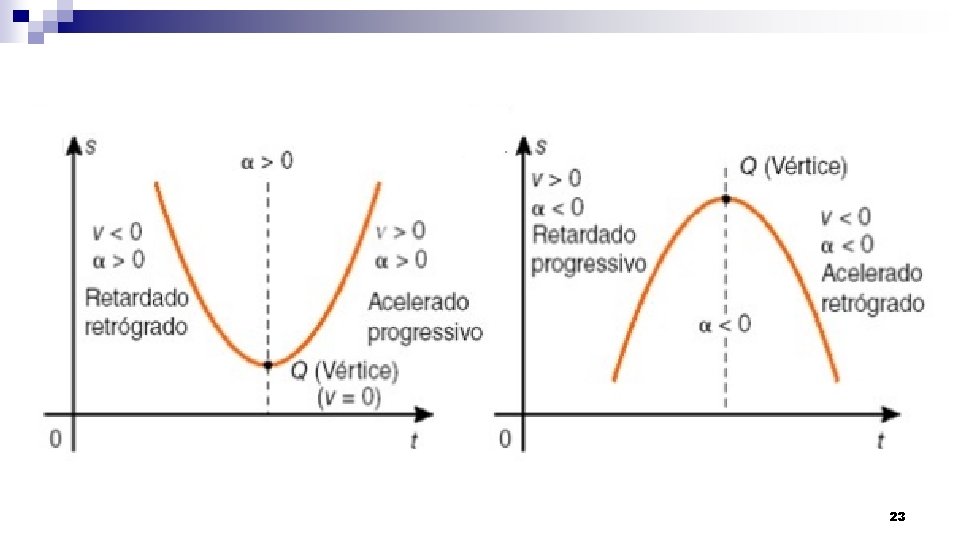
23

Situações Importantes Para MRU e MRUV Saída da origem: Caso o móvel esteja partindo da origem, ou problema não se refira à posição inicial (o que normalmente acontece), ela será zero (So = 0). n Passagem pela origem: Ao passar pela origem o espaço é sempre nulo. n Mudança de sentido: Quando o móvel muda de sentido, adote a velocidade final, como zero (v = 0). n 24

Situações Importantes Para MRU e MRUV n Encontro de móveis: dois ou mais móveis irão se encontrar quando suas posições se tornarem iguais, isto é, se os móveis A e B se encontrarem num instante t, então nesse instante: SA = SB 25

EXERCÍCIOS 2 - A função horária da posição de um móvel que se desloca sobre o eixo dos x é, no Sistema Internacional de Unidades, S = -10 + 4 t + t². A função horária da velocidade para o referido movimento é. a) v = 4 + 2. t b) v = 4 + t c) v = 4 + 0, 5. t d) v = -10 + 4. t e) v = -10 + 2. t

3 - A tabela fornece, em vários instantes, as velocidades de um móvel que, partindo da origem (x = 0 no instante t = 0), desloca-se em trajetória retilínea e em movimento uniformemente acelerado. A partir dessas informações podemos afirmar que, no S. I. , a função velocidade, v = f(t), e a função horária, x = f(t), desse movimento são, respectivamente: a) v = 3 t e x = 1, 5 t 2 b) v = 3 + 3 t e x = 3 t + 3 t 2 c) v = 1, 5 t e x = 3 t + 1, 5 t 2 d) v = 3 t e x = 3 t + 1, 5 t 2 e) v = 3 t e x = 3 t 2

4 - Um carro está parado em um semáforo, aguardando abrir o sinal. No instante em que acende a luz verde, ele parte com uma aceleração constante 5, 0 m/s². Um caminhão que vinha com velocidade constante de 10 m/s, trafegando no mesmo sentido do carro, passa por ele no exato momento da partida. Após quanto tempo o carro alcança o caminhão e qual é, a distância percorrida para alcançá-lo?

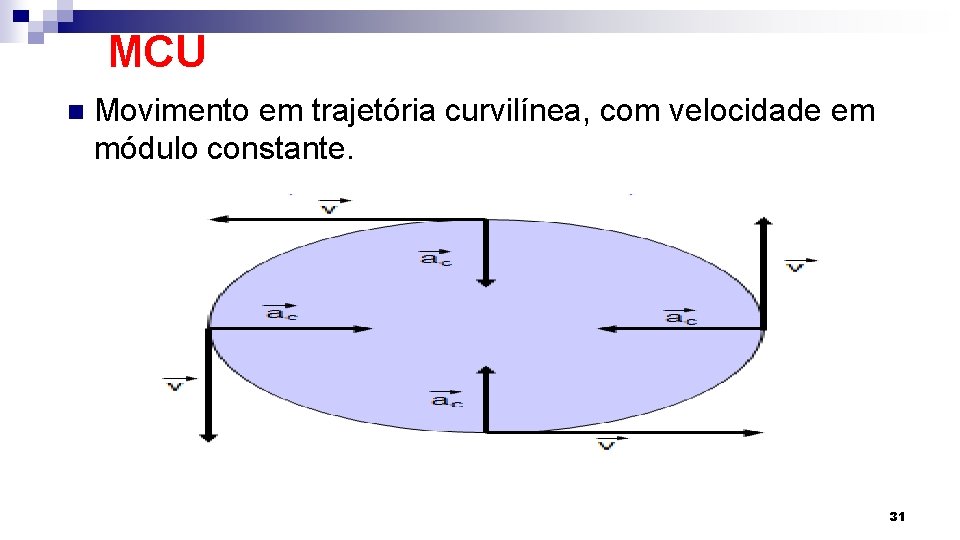
Movimento Curvílineo Uniforme (MCU) 1. A trajetória é uma circunferência. 2. A velocidade vectorial é constante em módulo e variável em direcção e sentido. 3. A aceleração tangencial é nula. 4. A aceleração centrípeta é constante em módulo e variável em direcção e sentido 29

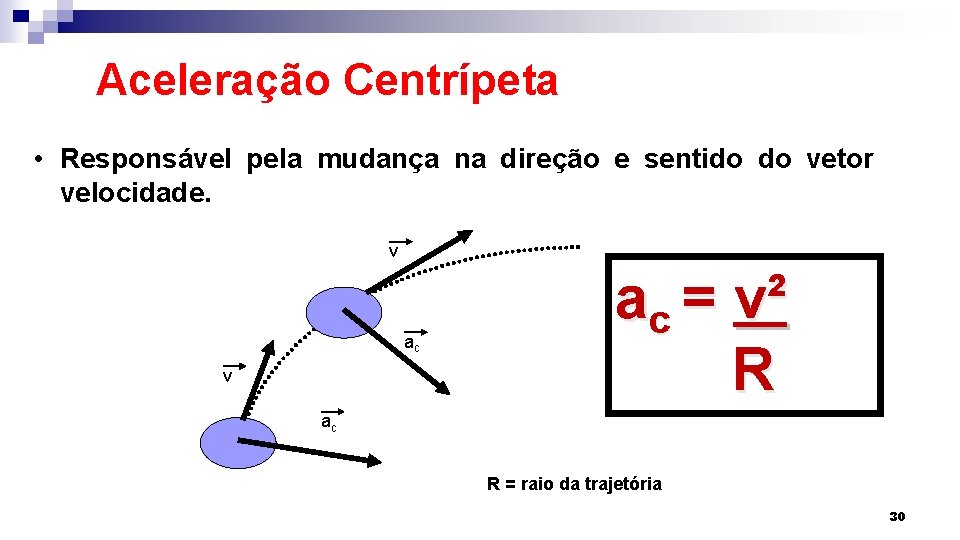
Aceleração Centrípeta • Responsável pela mudança na direção e sentido do vetor velocidade. v ac = v² R ac R = raio da trajetória 30

MCU n Movimento em trajetória curvilínea, com velocidade em módulo constante. 31

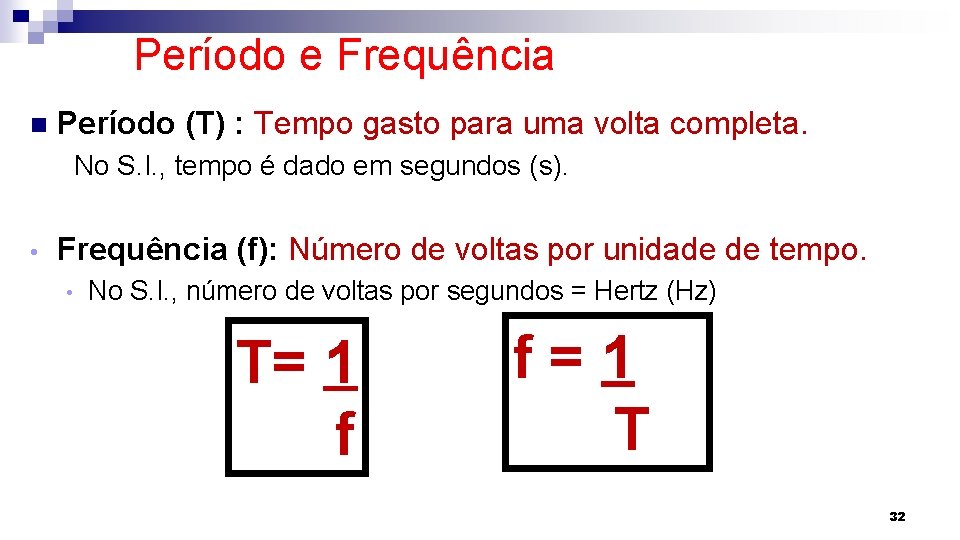
Período e Frequência n Período (T) : Tempo gasto para uma volta completa. No S. I. , tempo é dado em segundos (s). • Frequência (f): Número de voltas por unidade de tempo. • No S. I. , número de voltas por segundos = Hertz (Hz) T= 1 f f = 1 T 32

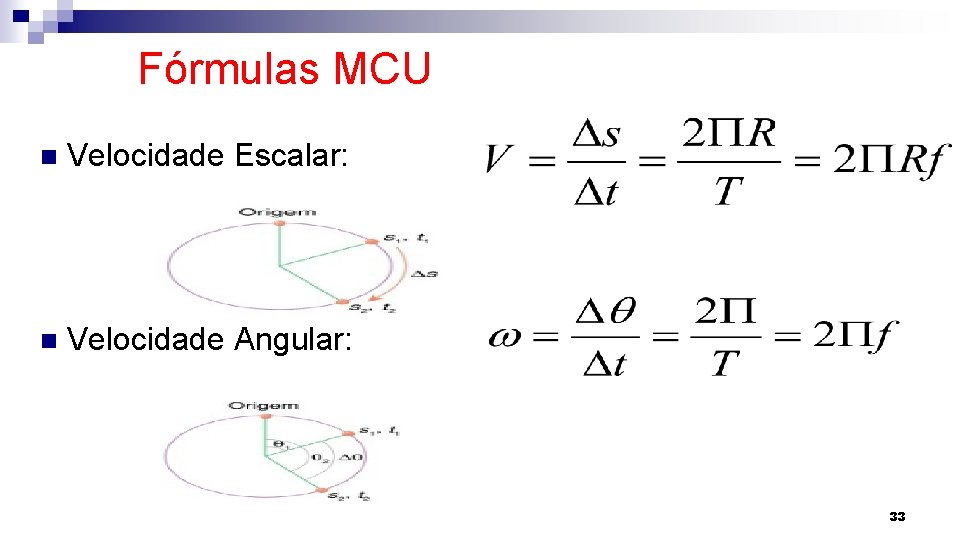
Fórmulas MCU n Velocidade Escalar: n Velocidade Angular: 33

Relação entre as Velocidades Escalar e Angular 34

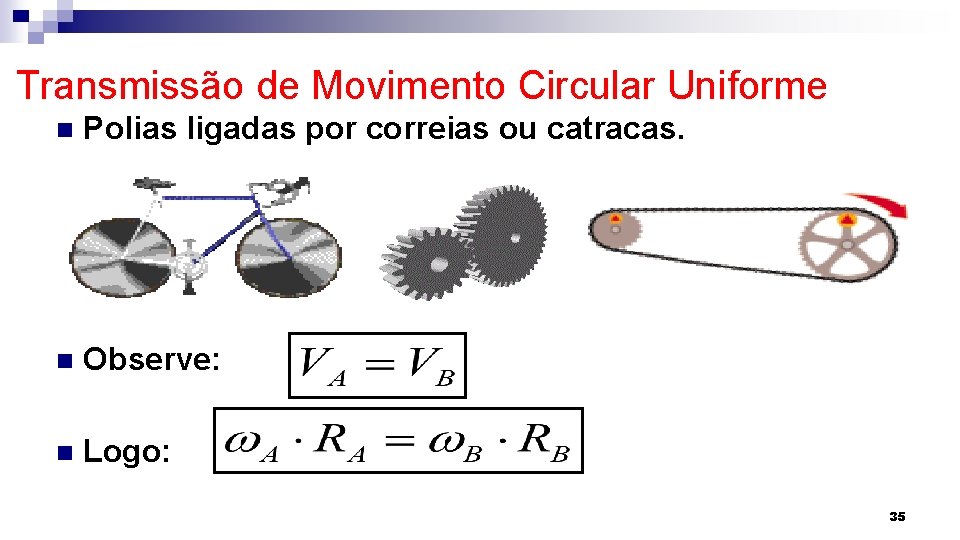
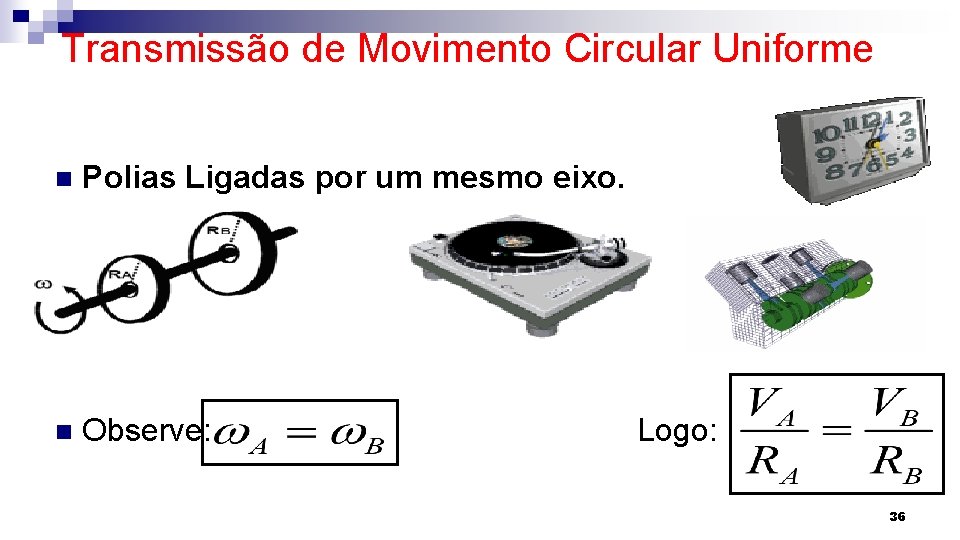
Transmissão de Movimento Circular Uniforme n Polias ligadas por correias ou catracas. n Observe: n Logo: 35

Transmissão de Movimento Circular Uniforme n Polias Ligadas por um mesmo eixo. n Observe: Logo: 36

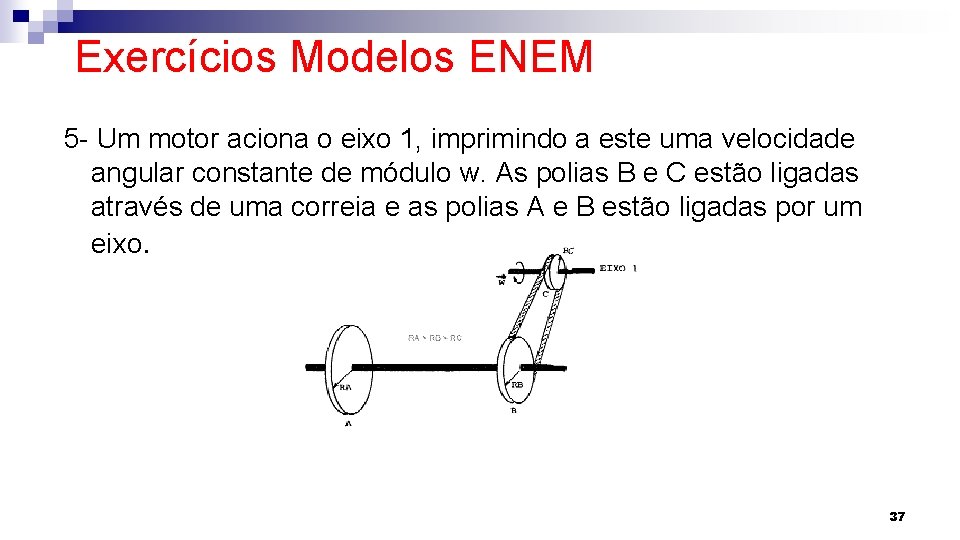
Exercícios Modelos ENEM 5 - Um motor aciona o eixo 1, imprimindo a este uma velocidade angular constante de módulo w. As polias B e C estão ligadas através de uma correia e as polias A e B estão ligadas por um eixo. 37

Com relação aos sistema, podemos afirmar que as velocidades periféricas tangenciais de módulo v e angulares de módulo w de cada polia são (A)v. B > v. C w. B = w. A (B)v. B = v. C w. B = w. A (C)v. B = v. C w. B > w. A (D)v. B < v. C w. B > w. A (E)v. B < v. C w. B = w. A 38

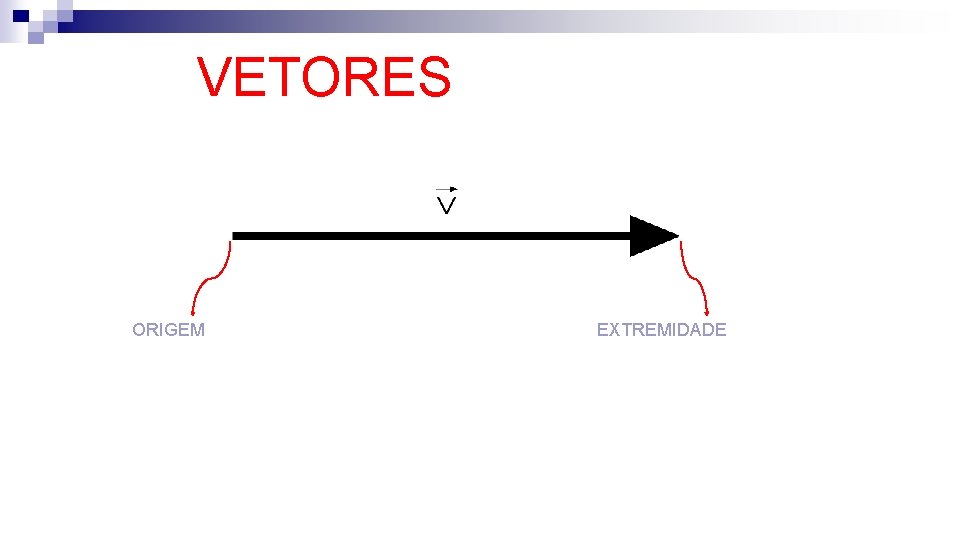
VETORES ORIGEM EXTREMIDADE

VETORES 1 - Vetores na mesma direção e sentido.

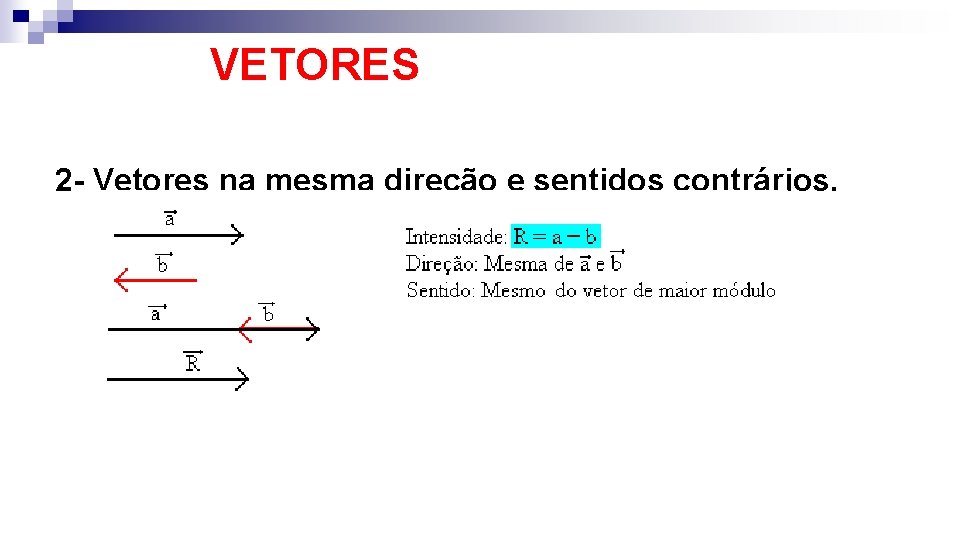
VETORES 2 - Vetores na mesma direção e sentidos contrários.

VETORES 3 - Vetores perpendiculares (90°) entre si.

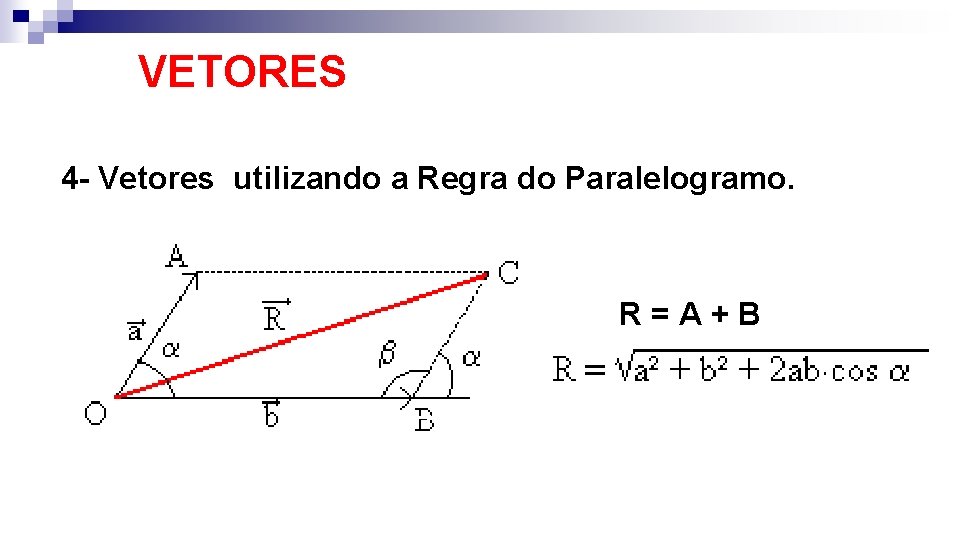
VETORES 4 - Vetores utilizando a Regra do Paralelogramo. R = A + B

Exemplo 6 -Verifique quais são as grandezas escalares e vetoriais nas afirmações abaixo. 1) O deslocamento de um avião foi de 100 km, na direção Norte do Brasil. 2) A área da residência a ser construída é de 120, 00 m 2. 3) A força necessária para colocar uma caixa de 10 kg em uma prateleira é de 100 N. 4) A velocidade marcada no velocímetro de um automóvel é de 80 km/h. 5) Um jogo de futebol tem um tempo de duração de 90 minutos. Assinale a alternativa que apresenta a seqüência correta. a) vetorial, escalar, vetorial, escalar. b) vetorial, escalar, vetorial, escalar. c) escalar, vetorial, escalar. d) vetorial, escalar, vetorial, escalar. e) escalar, vetorial, escalar. 44

Exercícios 7 - Considere dois vetores deslocamento, de módulos a e b, que são perpendiculares entre si. Sabendo-se que a = 8 cm e que o vetor resultante da soma dos dois vetores possui módulo igual a 10 cm, o módulo do vetor b é igual a: a) 2 cm b) 6 cm c) 10 cm d) 18 cm e) 36 cm

FÍSICA: DINAMICA FORÇAS, LEIS DE NEWTON, TRABALHO E ENERGIA

Efeitos da Força 1 - Deformação; 2 - Alteração da Velocidade; 3 - Equilíbrio.

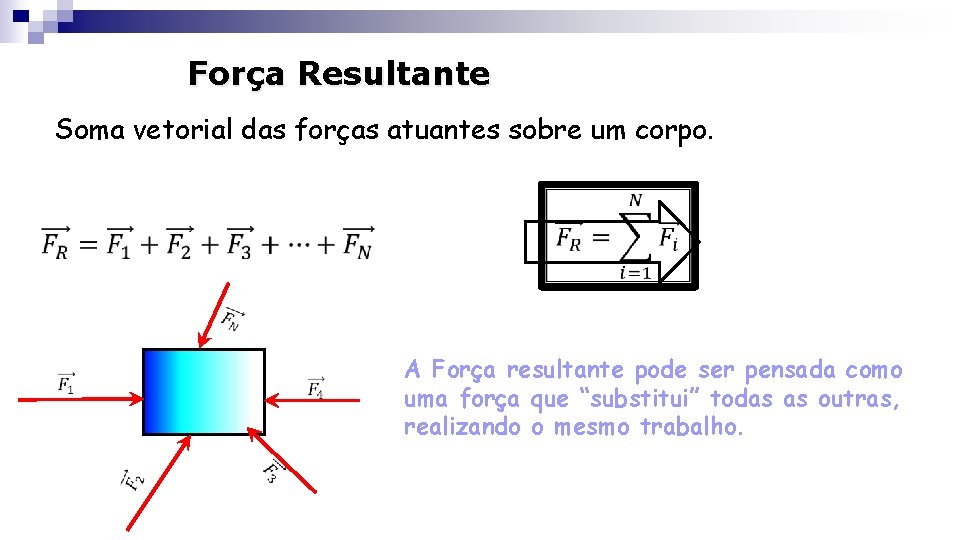
Força Resultante Soma vetorial das forças atuantes sobre um corpo. A Força resultante pode ser pensada como uma força que “substitui” todas as outras, realizando o mesmo trabalho.

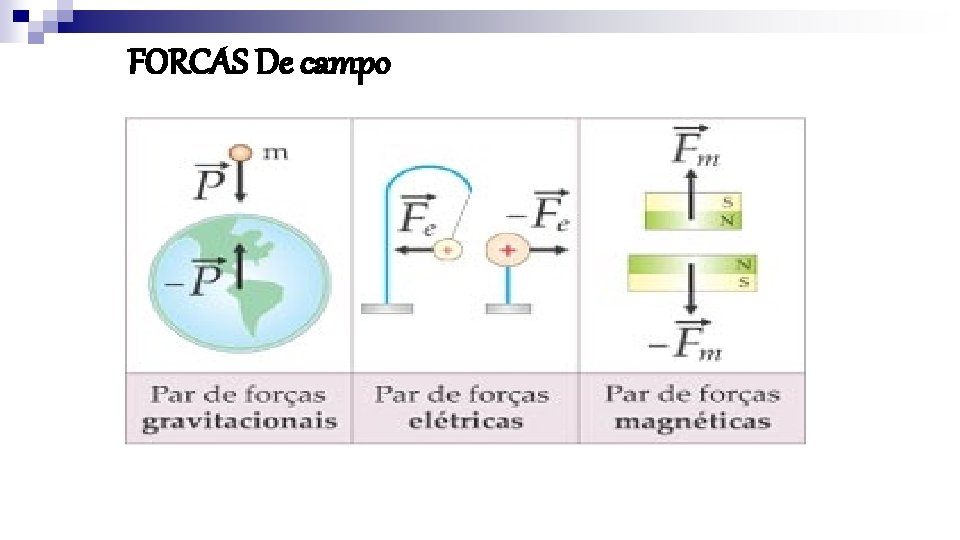
FORCAS De campo

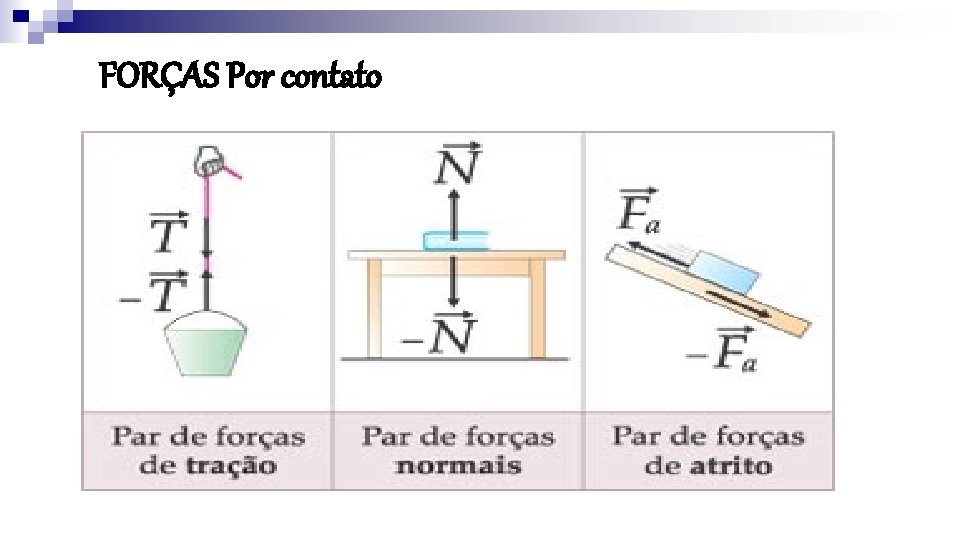
FORÇAS Por contato

1ª Lei de Newton – Lei da Inércia “Qualquer corpo tende a permanecer em seu estado de movimento ou de repouso se a resultante das forças que atuam sobre ele for nula. ” → REPOUSO ou MRU

2ª Lei de Newton – Lei Fundamental da Dinâmica “A Força Resultante sobre um corpo é igual ao produto da sua massa pela aceleração que adquire. ”

3ª Lei de Newton – Lei da Ação e Reação “A toda ação corresponde uma reação, de mesma intensidade, mesma direção, porém de sentido contrário atuando em corpos distintos. ”

1) As forças de ação e reação aparecem aos pares, sempre que dois corpos interagem; 2) Os pares ação/reação podem ser de contato direto ou de ação a distância sendo o par sempre da mesma natureza; 3) Os pares ação/reação nunca se anulam pois atuam em corpos diferentes.

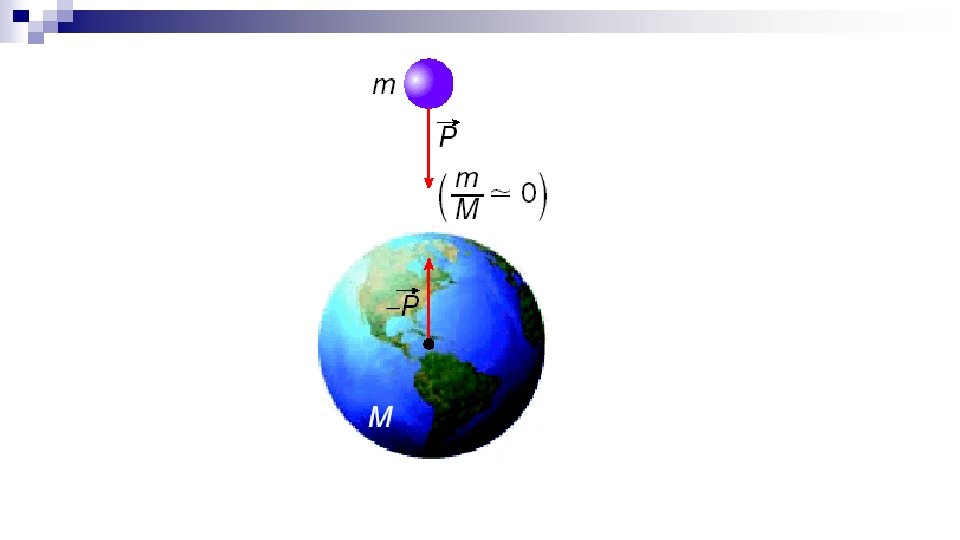
FORÇA PESO Newton postulou que todo corpo dotado de massa atrai outros corpos que também tenham massa. Essa força de atração é conhecida como força gravitacional. Todos os corpos na superfície da Terra são atraídos na direção do centro do nosso planeta com uma força que chamamos de PESO. g vale aproximadamente 10 m/s² na superfície da Terra.

EXEMPLOS 8 - O uso do cinto de segurança pode evitar tanto acidentes graves quanto mortes. Com base nas três leis de Newton, dentro do campo da Física, podemos explicar seu uso da seguinte forma: a) Considerando a massa (m) do cinto de segurança, podemos entender seu mecanismo baseado na 2ª lei de Newton, pois devido à desaceleração (a) do carro o cinto exercerá uma força sobre nosso corpo dada por: F = ma. b) O cinto de segurança pode ser entendido como um dispositivo usado para diminuir a aceleração do carro, portanto, está relacionado com a 2ª lei de Newton. c) O cinto de segurança é um dispositivo baseado na 3ª lei de Newton, pois o carro exerce uma força sobre o cinto e este reage, exercendo uma força sobre nosso corpo. d) O cinto de segurança é um dispositivo usado para neutralizar a lei da inércia, evitando que nosso corpo continue deslocando-se para frente, quando o carro diminui sua velocidade bruscamente.

EXEMPLOS 9 - Certo carro nacional demora 30 s para acelerar de 0 a 108 km/h. Supondo sua massa igual a 1200 kg, o módulo da força resultante que atua no veículo durante esse intervalo de tempo é, em Newton, igual a: a) zero. b) 1200 c) 3600 d) 4320 e) 36000

EXEMPLOS 10 - Observe a tira abaixo: A forma encontrada por Garfield para perder peso é: a) correta, uma vez que, em um planeta de gravidade menor, seu peso será realmente menor, porém com a mesma massa. b) errada, pois em um planeta de gravidade menor sua massa será maior, porém com o mesmo peso. c) correta, pois em um planeta de gravidade menor sua massa será menor, porém seu peso será maior. d) correta, pois em um planeta de gravidade menor sua massa e seu peso serão maiores. e) correta, pois em um planeta de gravidade menor sua massa e seu peso serão menores.

Força Normal Surge quando um corpo se encontra sobre certa superfície de apoio. A força peso e a normal não formam um par ação e reação.

Força Normal É a força de reação que a superfície exerce sobre o corpo que a comprime. É necessário a presença de uma superfície, e nem sempre é igual ao peso do corpo. O valor da Força Normal é igual ao da Força Peso quando a superfície for perfeitamente perpendicular ao campo gravitacional (horizontal) e não houverem outras forças atuando na mesma direção da Força Peso.

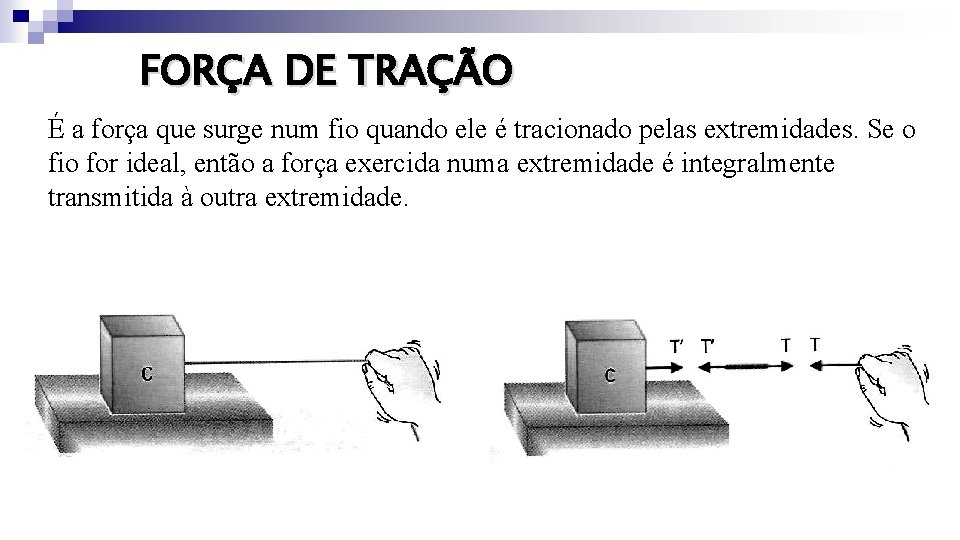
FORÇA DE TRAÇÃO É a força que surge num fio quando ele é tracionado pelas extremidades. Se o fio for ideal, então a força exercida numa extremidade é integralmente transmitida à outra extremidade.

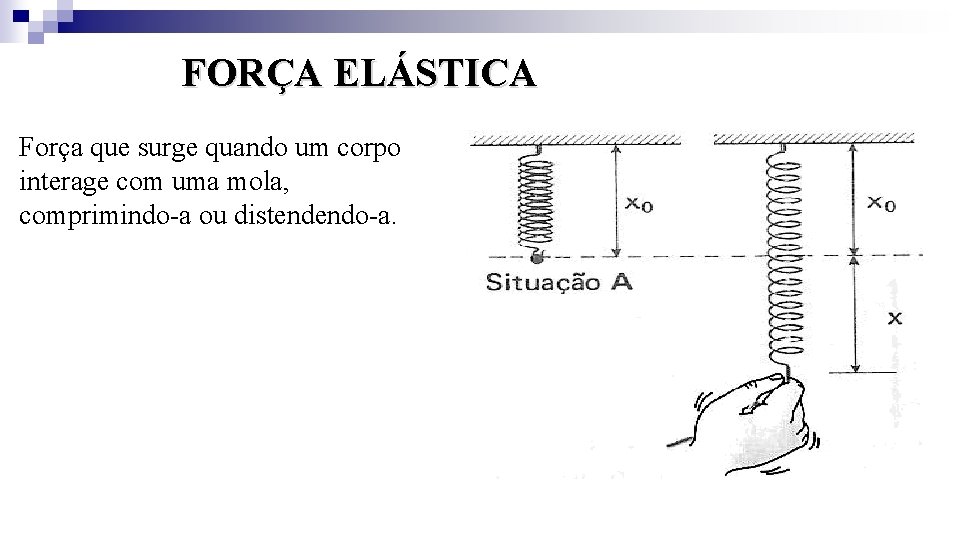
FORÇA ELÁSTICA Força que surge quando um corpo interage com uma mola, comprimindo-a ou distendendo-a.

LEI DE HOOK Relaciona a deformação sofrida por uma mola com a força nela aplicada e a sua natureza, expressa pela chamada constante elástica da mola. F = k. x

x→ deformação da mola (m) k → constante elástica da mola (N/m) F → Força aplicada (N)

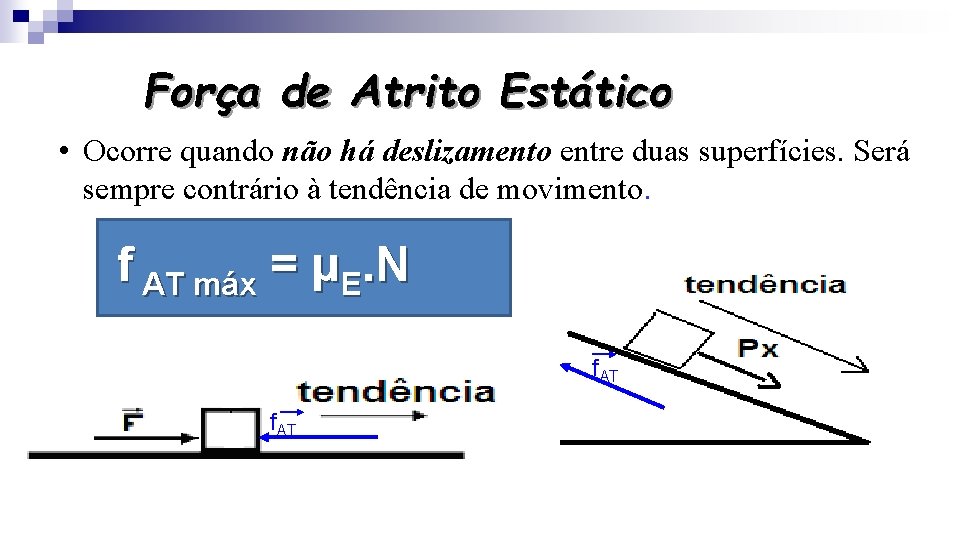
Força de Atrito Estático • Ocorre quando não há deslizamento entre duas superfícies. Será sempre contrário à tendência de movimento. f AT máx = μE. N f. AT

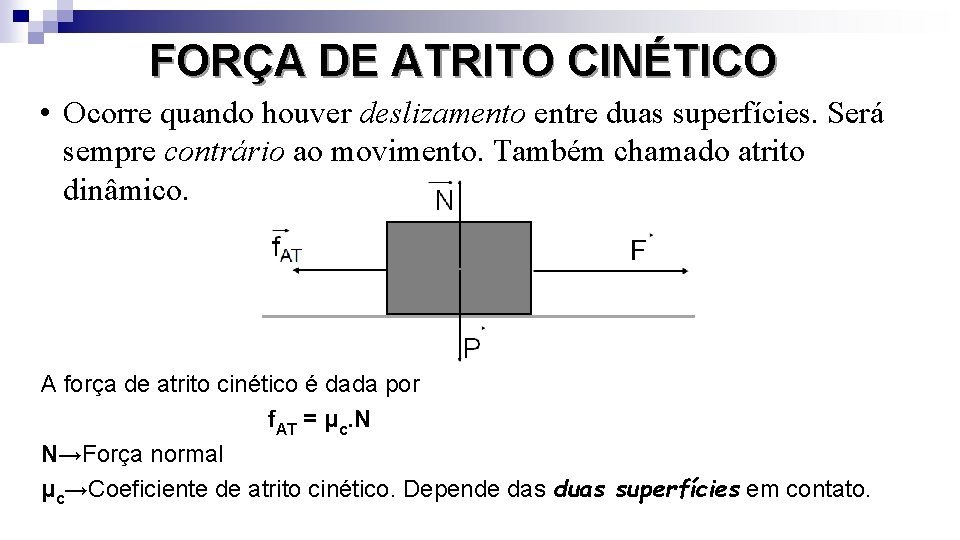
FORÇA DE ATRITO CINÉTICO • Ocorre quando houver deslizamento entre duas superfícies. Será sempre contrário ao movimento. Também chamado atrito dinâmico. A força de atrito cinético é dada por f. AT = μc. N N→Força normal μc→Coeficiente de atrito cinético. Depende das duas superfícies em contato.

ATRITO PREJUDUCIAL - O atrito entre os móveis e o chão dificulta o seu movimento. - O atrito entre as peças de uma máquina provoca o seu desgaste. ATRITO ÚTIL O atrito entre os pneus dos carros e o solo permite-lhes acelerar, travar e parar. O atrito entre os sapatos e o chão permite-nos andar. O atrito entre os objetos e as mãos permite segurá-los. O atrito entre a borracha e o papel permite apagar os riscos do lápis. O atrito entre o giz e o quadro permite escrever.

Macetes para resolução de problemas 1. Faça um esquema/desenho simples da situação. 2. Escolha um sistema de referência (sistema de coordenadas x, y). 3. Isole os corpos e faça um diagrama das forças atuantes em cada corpo. Lembre-se de que: • Se o corpo tem massa, existirá uma Força Peso. P = mg • Se o corpo está em contato com a superfície, terá uma Força Normal perpendicular à superfície. • Se existem fios puxando corpos, existirão Forças de Tração.

Trabalho de uma força, Trabalho da força peso, Trabalho da força elástica

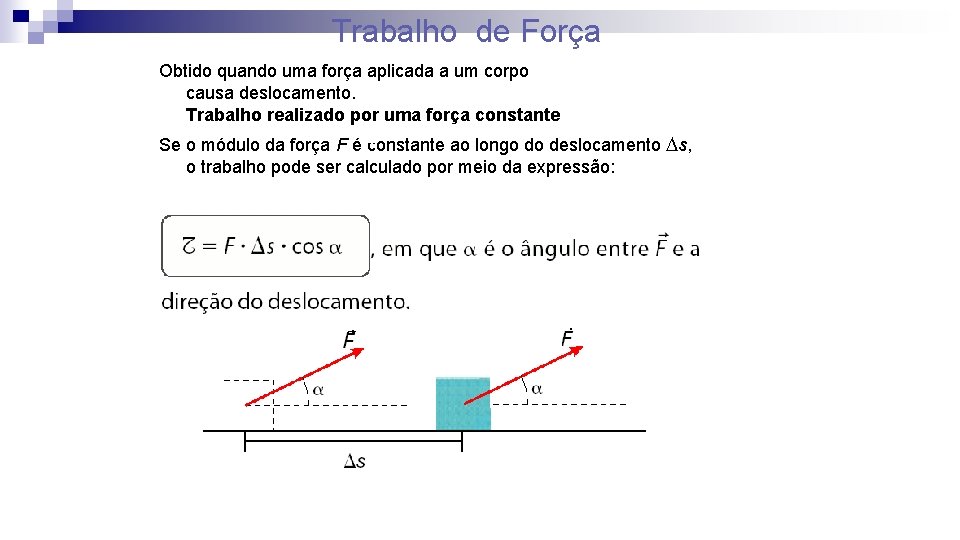
TRABALHO DE FORÇA O trabalho de uma força é definido como uma grandeza escalar correspondente ao produto da força pelo deslocamento, desde que a força e o deslocamento tenham mesma direção e sentido. Em que: = F. d F é a força. é o trabalho. No S. I. : 1 - a força F é medida em newtons (N); 2 - o deslocamento d é medido em metros (m); 3 - o trabalho é medido em joule (J).

Trabalho de Força Obtido quando uma força aplicada a um corpo causa deslocamento. Trabalho realizado por uma força constante Se o módulo da força F é constante ao longo do deslocamento s, o trabalho pode ser calculado por meio da expressão:

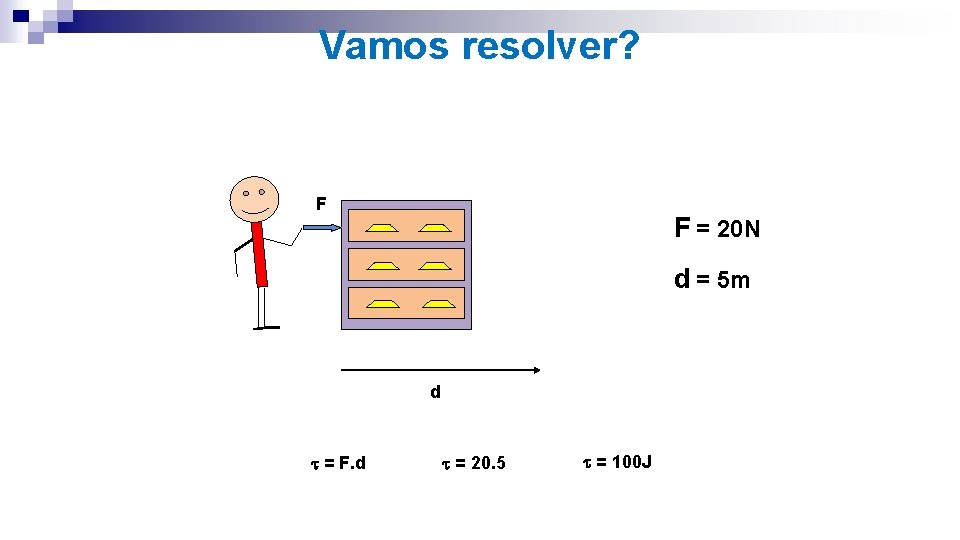
11 - Um garoto empurra uma cômoda durante um certo intervalo de tempo e consegue deslocá-la por 5 m. Sabendo que a força aplicada tem módulo de 20 N e foi aplicada na mesma direção e sentido do deslocamento, determine o valor do trabalho realizado pela força.

Vamos resolver? F F = 20 N d = 5 m d = F. d = 20. 5 = 100 J

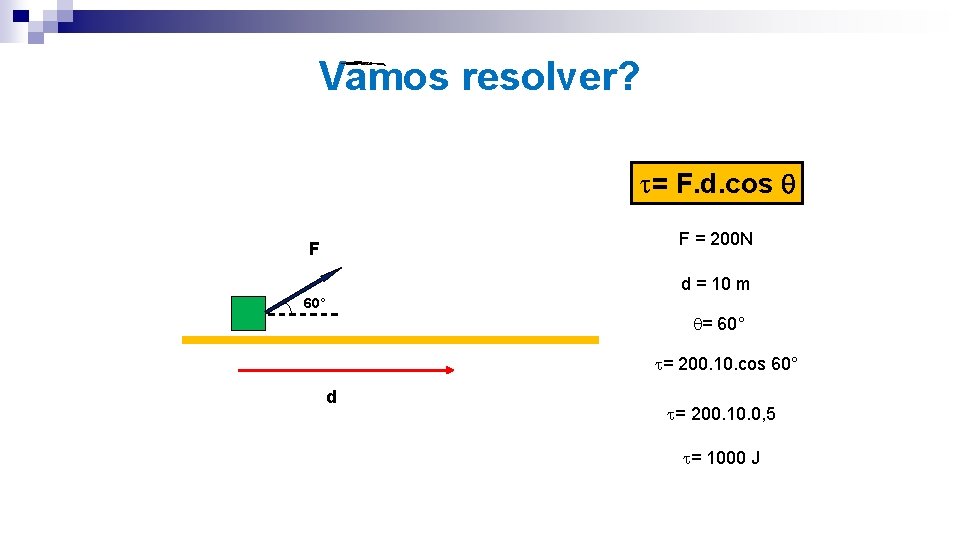
12 - Durante um trabalho em um armazém, um homem puxa um caixote com uma força de 200 N que forma um ângulo de 60° com a horizontal, direção na qual ocorre um deslocamento de 10 m. Determine o trabalho realizado pela força aplicada pelo homem.

Vamos resolver? t= F. d. cos F = 200 N F d = 10 m 60° = 60° t= 200. 10. cos 60° d t= 200. 10. 0, 5 t= 1000 J

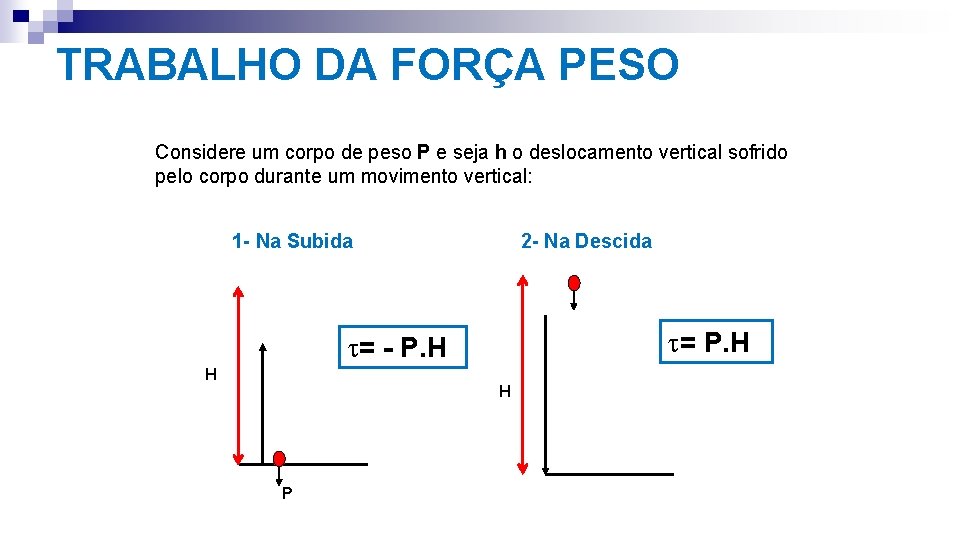
TRABALHO DA FORÇA PESO Trabalho da força peso t = P · h Þt = m · g · h P Trabalho da força peso é P positivo, quando o corpo desce negativo, quando o corpo sobe 11. 3

TRABALHO DA FORÇA PESO Considere um corpo de peso P e seja h o deslocamento vertical sofrido pelo corpo durante um movimento vertical: 1 - Na Subida 2 - Na Descida t= P. H t= - P. H H H P

o trabalho da força peso independe da trajetória adotada pelo corpo, isto é, depende apenas da altura e do peso do corpo: OBS. : t. I = II= III P H I II III

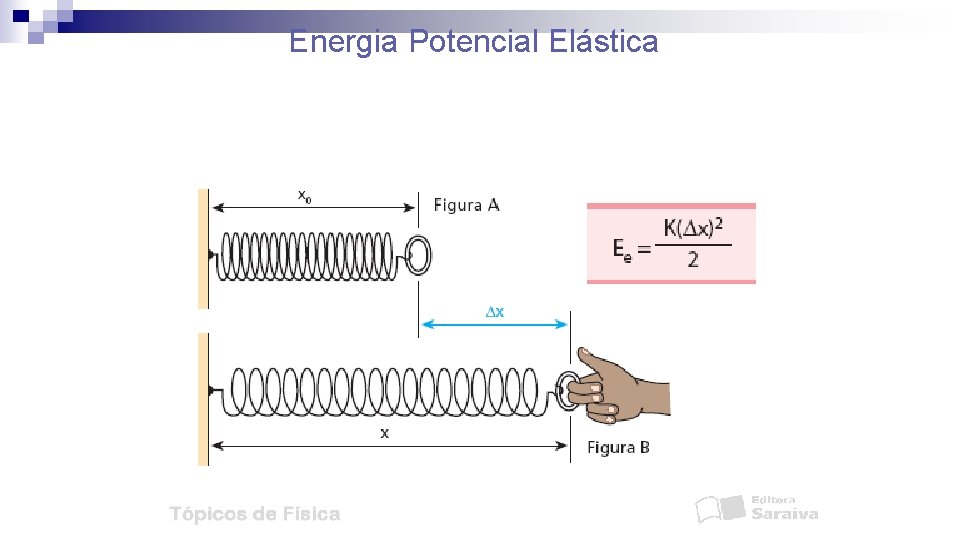
FÍSICA, 1º Ano do Ensino Médio Trabalho de uma Força TRABALHO DA FORÇA ELÁSTICA Observe que, quando uma mola sofre deformações em regime elástico aplicando-lhe uma força F, surge uma força elástica Fel em sentido oposto que tende a trazer a mola à sua posição inicial de repouso: Em que: F = Fel X Fel = K. X Fel F K é constante elástica da mola; X é deformação sofrida pela mola.

Ʈ= ± KX 2 2 OBS. 1: o trabalho da força elástica é positivo quando a mola está voltando para a posição inicial, pois o deslocamento (deformação X) e a força elástica têm mesma direção e sentido. OBS. 2: o trabalho da força elástica é negativo quando a mola está sendo deformada, pois o deslocamento (deformação X) e a força elástica têm mesma direção e sentido opostos.

Energia

Formas fundamentais de energia As diferentes designações atribuídas à energia correspondem apenas a duas formas fundamentais de energia: ü Energia cinética que está associada ao movimento. Esta é a energia que associamos ao vento, à água em movimento, à corrente eléctrica no circuito, ao som e à agitação das partículas do ar junto de um aquecedor. ü Energia potencial que corresponde à energia armazenada em condições de poder ser utilizada. Esta é a energia acumulada numa bateria, nos alimentos e nos combustíveis.

ENERGIA CINÉTICA Manifesta-se no movimento dos corpos em relação a um dado referencial. O corpo em questão deve apresentar velocidade diferente de zero no instante em que estiver sendo observado. em que m é a massa do corpo, e v, o módulo de sua velocidade.

Energia Potencial Gravitacional Energia potencial gravitacional: manifesta-se quando um corpo se encontra a determinada altura em relação a um nível referencial. Usina hidrelétrica: no ponto mais alto da queda-d´água, a energia potencial tem seu maior valor.

Energia potencial O alpinista possui energia armazenada pelo fato de estar a ser atraído pela Terra. Essa energia que não se está a manifestar mas que pode vir a manifestar-se se cair, designa-se por energia potencial gravítica.

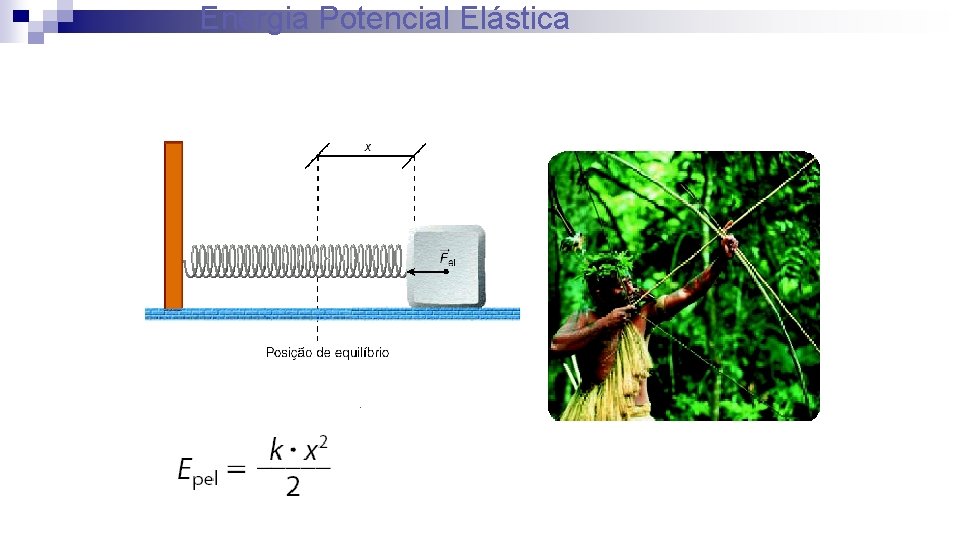
Energia Potencial Elástica

Energia Potencial O boneco dentro da caixa tem energia armazenada. Esta energia manifesta-se quando o boneco salta e designa-se por energia potencial elástica.

Energia Potencial Elástica

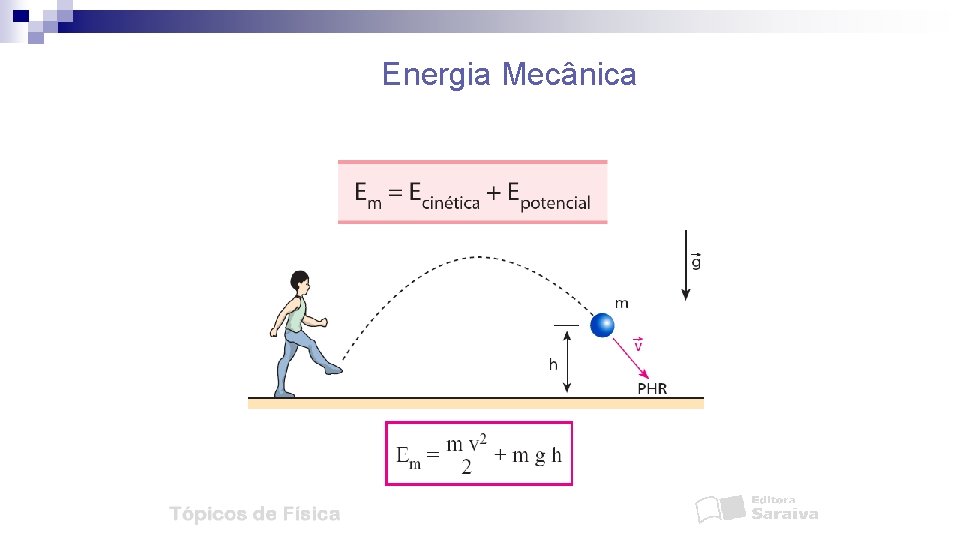
Energia Mecânica É a soma de todas as energias potenciais com a energia cinética.

Energia Mecânica

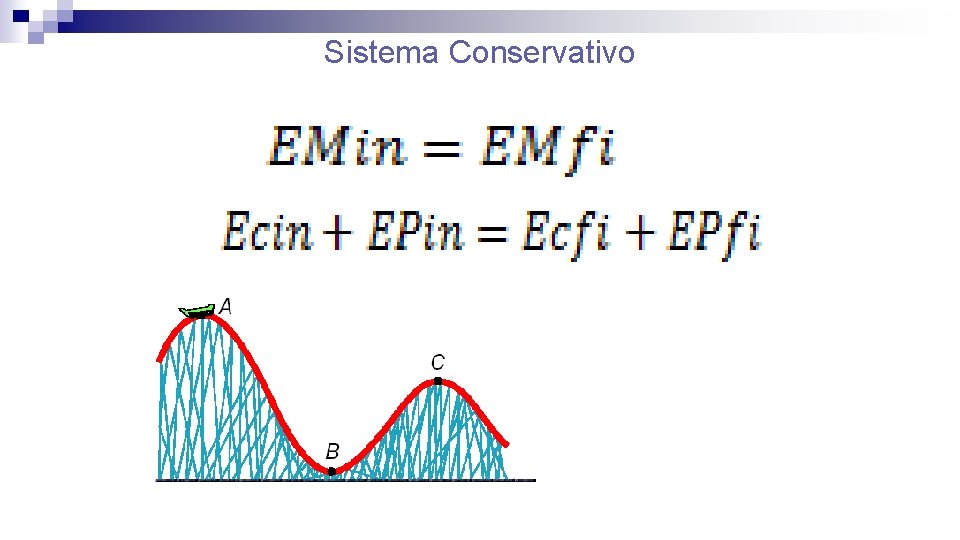
Sistema Conservativo

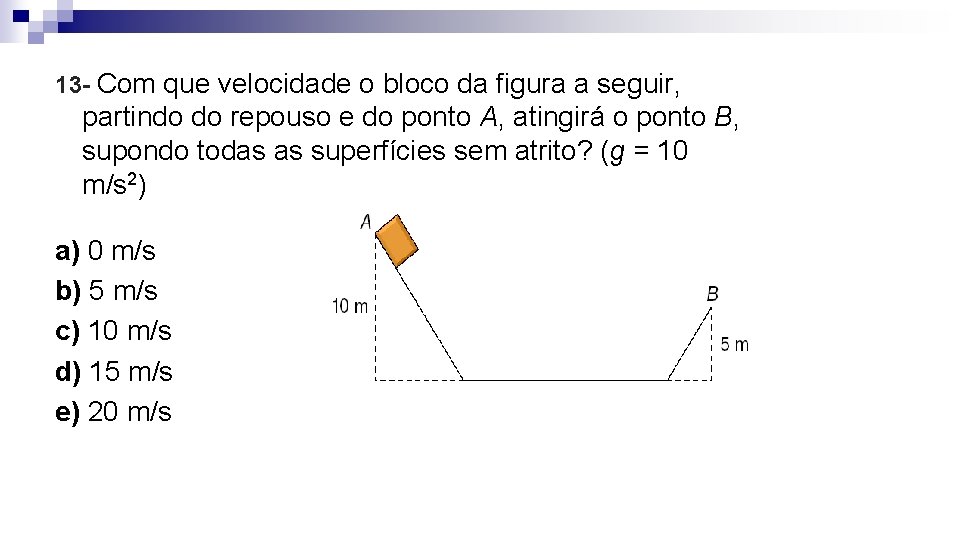
13 - Com que velocidade o bloco da figura a seguir, partindo do repouso e do ponto A, atingirá o ponto B, supondo todas as superfícies sem atrito? (g = 10 m/s 2) a) 0 m/s b) 5 m/s c) 10 m/s d) 15 m/s e) 20 m/s

Sistema não Conservativo 14 - Um corpo de massa 400 gramas despenca, sem velocidade, do topo de um prédio de altura 20 metros, atingindo o solo com velocidade de 10 m/s. Usando g = 10 m/s², calcule a energia mecânica dissipada nesta queda.

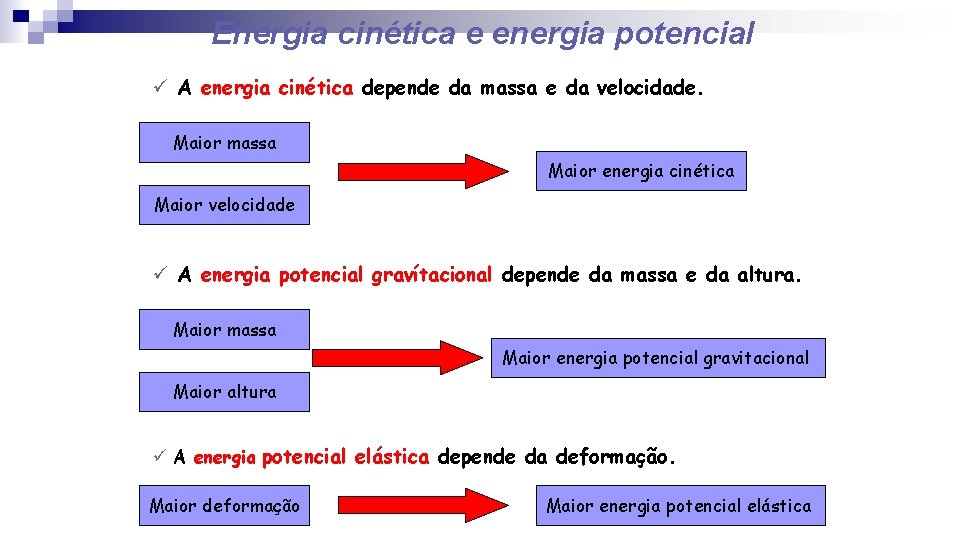
Energia cinética e energia potencial ü A energia cinética depende da massa e da velocidade. Maior massa Maior energia cinética Maior velocidade ü A energia potencial gravítacional depende da massa e da altura. Maior massa Maior energia potencial gravitacional Maior altura ü A energia potencial elástica depende da deformação. Maior deformação Maior energia potencial elástica

FÍSICA TERMOLOGIA, DILATAÇÃO, CALORIMETRIA

TERMOLOGIA é a parte da Física que estuda os fenômenos relacionados com o calor e a temperatura. Imagem: Fir 0002, flagstaffotos. com. au / GNU Free Documentation License / http: //commons. wikimedia. org/wiki/File: Fire 02. jpg Imagem: Gérald Tapp / Creative Commons Attribution-Share Alike 3. 0 Unported

TEMPERATURA: GRAU DE AGITAÇÃO MOLECULAR. CALOR: ENERGIA TÉRMICA EM MOVIMENTO.

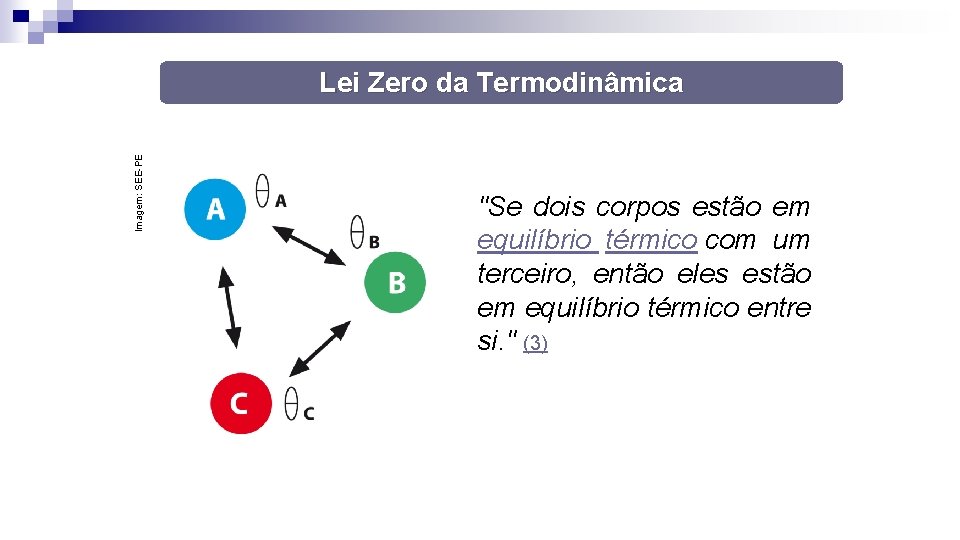
Imagem: SEE-PE Lei Zero da Termodinâmica "Se dois corpos estão em equilíbrio térmico com um terceiro, então eles estão em equilíbrio térmico entre si. " (3)

Graduação de um termômetro Termômetro: É um aparelho que permite medir a temperatura dos corpos. Seu processo baseia-se no equilíbrio térmico. Para graduação de um termômetro é necessário definir os pontos fixos, ambos sob pressão normal. n n 1 o Ponto Fixo: Corresponde a temperatura de fusão do gelo. 2 o Ponto Fixo: Corresponde a temperatura de ebulição da água. Apresentação do Termômetro

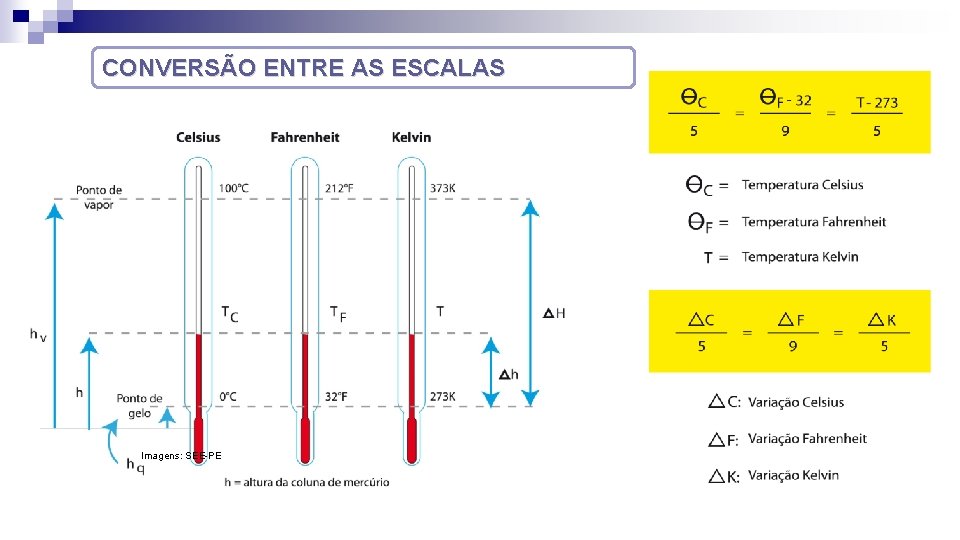
CONVERSÃO ENTRE AS ESCALAS Imagens: SEE-PE

Relações entre as escalas

Dilatação Térmica – Linear Exemplos:

Tipos de Dilatação Térmica " Se o espaço entre as partículas aumenta, o volume final do corpo acaba aumentando também“ "Se o espaço entre as partículas diminui, o volume final do corpo acaba diminuindo também“ A dilatação/contração térmica pode ser analisada por meio de três formas: - Linearmente - Superficialmente - Volumétricamente

Dilatação Linear É a dilatação que ocorre em uma dimensão do corpo. A constante de proporcionalidade é considerada coeficiente de dilatação linear. L Lo e L T L depende do material que constitui o corpo. Logo: L = L – Lo L = Lo. . T Onde: L = variação do comprimento L = L – Lo Lo = comprimento inicial = coeficiente de dilatação linear T = variação da temperatura T= T – To

Coeficiente de Dilatação Linear = L / (Lo. T) Cuja Unidade será: = 1/ o. C = o. C-1 Isolando “ ” teremos: Exemplos: Alumínio 23. 10 -6 o. C-1 Cobre 17. 10 -6 o. C-1 Vidro 9. 10 -6 o. C-1 Vidro Pirex 3, 2. 10 -6 o. C-1 Zinco 25. 10 -6 o. C-1 Chumbo 29. 10 -6 o. C-1 Aço 11. 10 -6 o. C-1

Exemplo: n 15 - A dilatação térmica dos sólidos é um fenômeno importante em diversas aplicações de engenharia, como construções de pontes, prédios e estradas de ferro. Considere o caso dos trilhos de trem serem de aço, cujo coeficiente de dilatação é α = 11. 10 -6 °C-1. Se a 10°C o comprimento de um trilho é de 30 m, de quanto aumentaria o seu comprimento se a temperatura aumentasse para 40°C? RESOLUÇÃO: O cálculo da dilatação linear ΔL, do trilho é: ΔL = L 0. α. ΔT ΔL = 30. (11. 10 -6). (40 – 10) = 99. 10 -4 m n ou 0, 0099 m

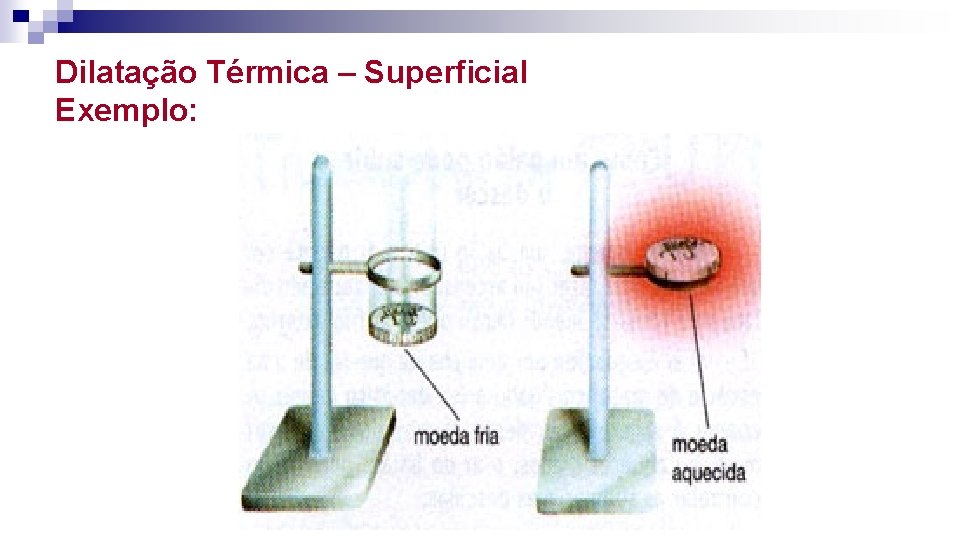
Dilatação Térmica – Superficial Exemplo:

Dilatação Superficial È a dilatação que ocorre em duas dimensões do corpo. A constante de proporcionalidade é considerada coeficiente de dilatação superficial. A Ao A T A depende do material que constitui o corpo. Logo: A = A – Ao A = Ao. . T Onde: A = variação da área A = A – Ao Ao = área inicial = coeficiente de dilatação superficial t = variação da temperatura T= T – To

Coeficiente de Dilatação Superficial Relação entre Coeficientes =2. Exemplos: Se Alumínio = 23. 10 -6 o. C-1 será 46. 10 -6 o. C-1 Se Cobre = 17. 10 -6 o. C-1 será 34. 10 -6 o. C-1

Exemplo: 16 -Uma chapa possui área de 4 m 2 a 0 o. C. Aquecendo-se a chapa a 50 o. C, de quanto aumenta a área da chapa e qual deverá ser sua área final. Dado = 10. 10 -6 o. C-1 ΔA = A 0. β. ΔT Obs. : β = 2. α ΔA = 4. (2 x 10. 10 -6). (50 – 0) = 0, 004 m 2 A = 4 + 0, 004 = 4, 004 m 2

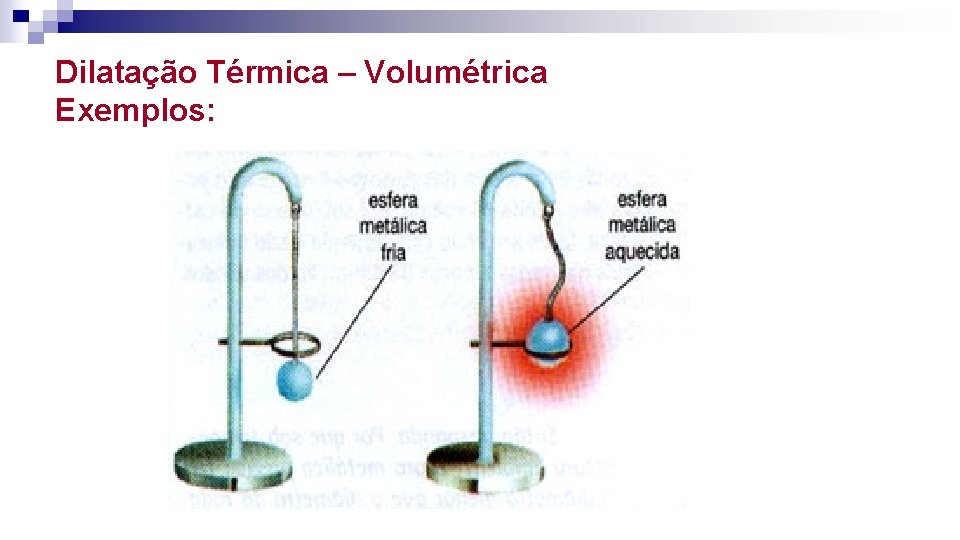
Dilatação Térmica – Volumétrica Exemplos:

Dilatação Térmica – Volumétrica Exemplos: Dilatação dos Gases Num balão de vidro, com ar em seu interior, introduz-se um canudo dentro do qual há uma gota de óleo. Segurando o balão de vidro como indicado na figura, o calor fornecido pelas mãos é suficiente para aumentar o volume de ar e deslocar a gota de óleo.

Dilatação Volumétrica È a dilatação que ocorre em três dimensões do corpo. A constante de proporcionalidade é considerada coeficiente de dilatação volumétrica. V Vo e V T V depende do material que constitui o corpo. Logo: V = V – Vo V = Vo. . T Onde: V = variação do volume V = V – Vo Vo = comprimento inicial = coeficiente de dilatação linear T = variação da temperatura T = T – To

Coeficiente de Dilatação Volumétrico Relação entre Coeficientes =3. /1 = /2 = /3 Exemplos: Se Alumínio = 23. 10 -6 o. C-1 será 69. 10 -6 o. C-1 Se Cobre = 17. 10 -6 o. C-1 será 51. 10 -6 o. C-1

Exemplo: 17 - O volume de uma esfera metálica, a certa temperatura. é 100 cm 3. Que variação de volume sofrerá sob o acréscimo de 40 o. C de temperatura. Suponha ser constante e igual a 1. 10 -5 o. C-1 o coeficiente de dilatação linear do material de que é feita a esfera. ΔV = V 0. γ. ΔT Obs. : γ = 3. α ΔV = 100. (3 x 1. 10 -5). 40 = 0, 12 cm 3

Os anjos existem, mas algumas vezes não possuem asas e passamos a chamá-los de amigos. . . Respeite as diferenças!

CALORIMETRIA

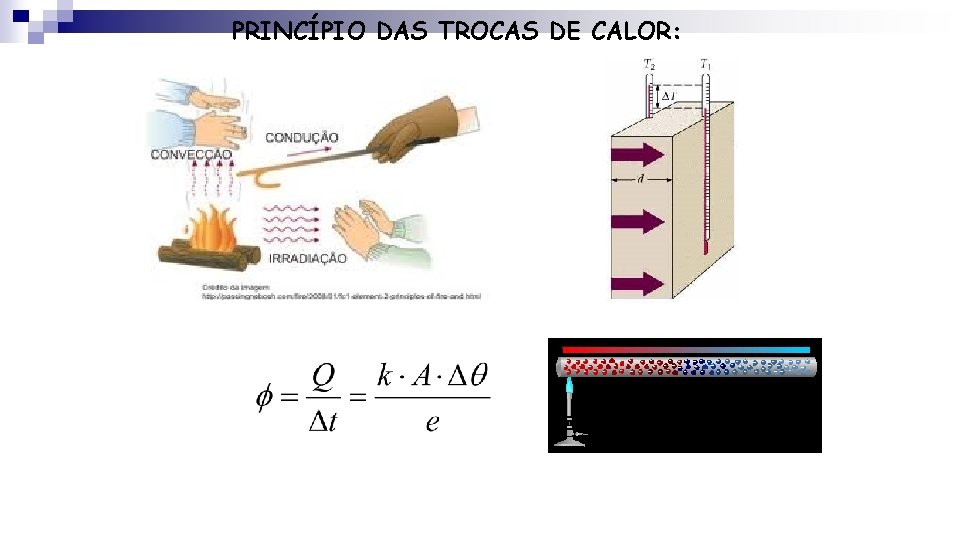
PRINCÍPIO DAS TROCAS DE CALOR:

Calorimetria A Calorimetria é a parte da Termologia que estuda o calor e suas medidas. Caloria ( cal ), a mais usada. Joule ( J ), a unidade oficial do Sistema Internacional de Unidades ( S. I ). ATENÇÃO: 1 cal = 4, 18 J

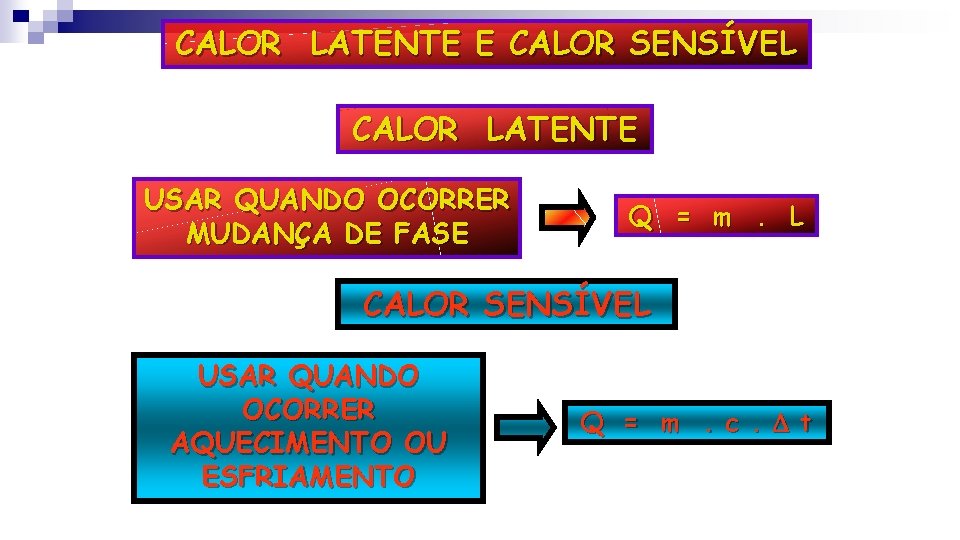
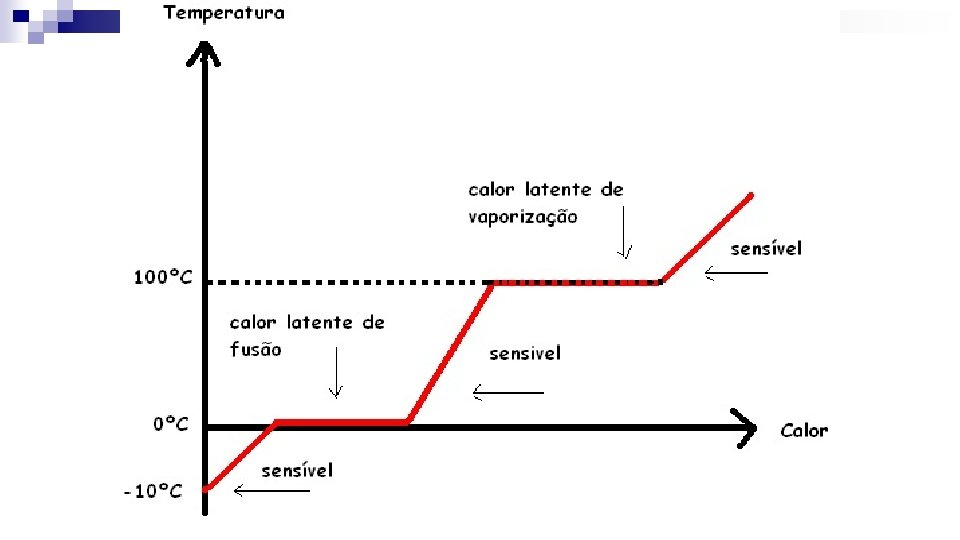
CALOR LATENTE E CALOR SENSÍVEL CALOR LATENTE USAR QUANDO OCORRER MUDANÇA DE FASE Q = m. L CALOR SENSÍVEL USAR QUANDO OCORRER AQUECIMENTO OU ESFRIAMENTO Q = m. c. t

Lembre-se : Para o calor Latente Q = Quantidade de calor necessária a mudança de fase quando a substância está no ponto. m = Massa da substância L = Calor latente da substância

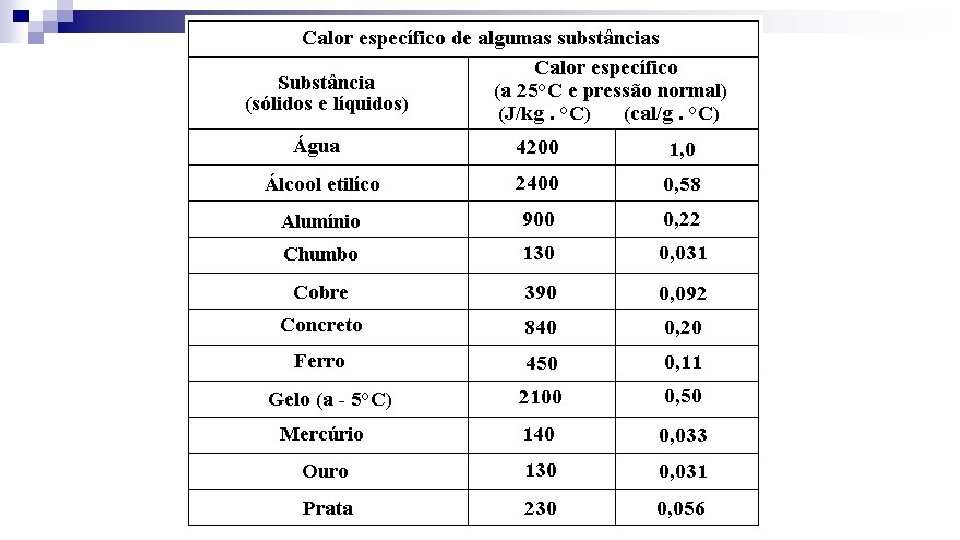
Lembre-se : Para o Calor sensivel Q = Quantidade de calor necessária para a mudança de temperatura do corpo m = Massa da substância c = calor especifico da substancia

18 - Calcule a quantidade de calor necessária para transformar 100 g de gelo a - 10 o C em água a 20 o ? Dados: calor específico do gelo = 0, 5 cal / g o. C calor latente de fusão do gelo = 80 cal / g calor específico da água = 1 cal / g o. C 1 a parte: Solução: O gelo se encontra numa temperatura abaixo do ponto de fusão, neste caso será aquecido de - 10 o C até o seu ponto de fusão (0 o C): Q =m. c. t Q 1 = m. c. t Q 1 = 100. 0, 5. (0 - (-10)) Q 1 = 50. (10 ) Q 1 = 500 cal

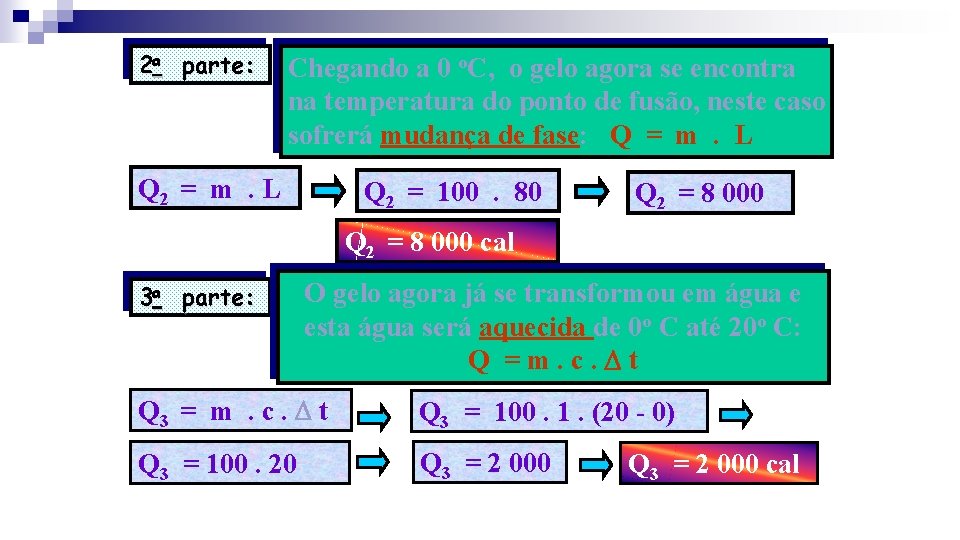
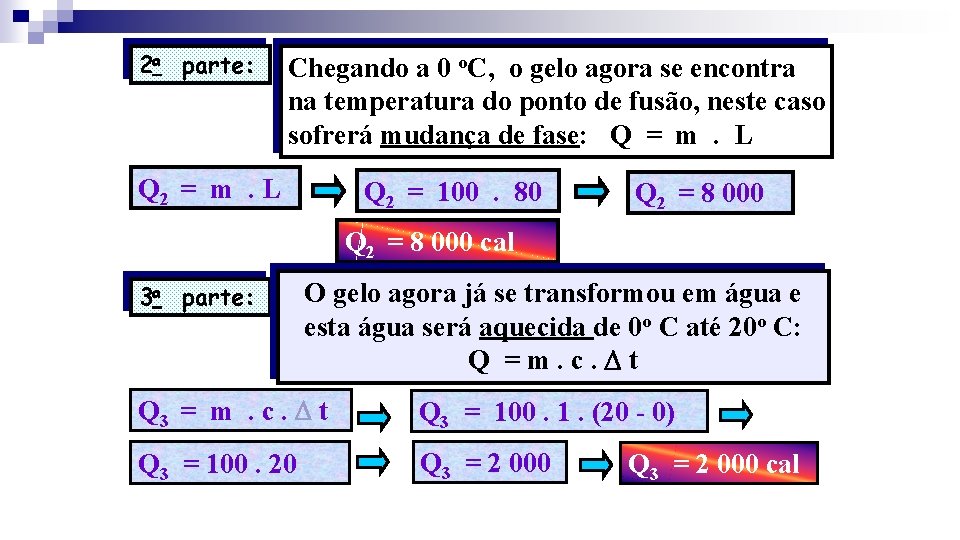
2 a parte: Chegando a 0 o. C, o gelo agora se encontra na temperatura do ponto de fusão, neste caso sofrerá mudança de fase: Q = m. L Q 2 = 100. 80 Q 2 = 8 000 cal 3 a parte: O gelo agora já se transformou em água e esta água será aquecida de 0 o C até 20 o C: Q =m. c. t Q 3 = m. c. t Q 3 = 100. 1. (20 - 0) Q 3 = 100. 20 Q 3 = 2 000 cal

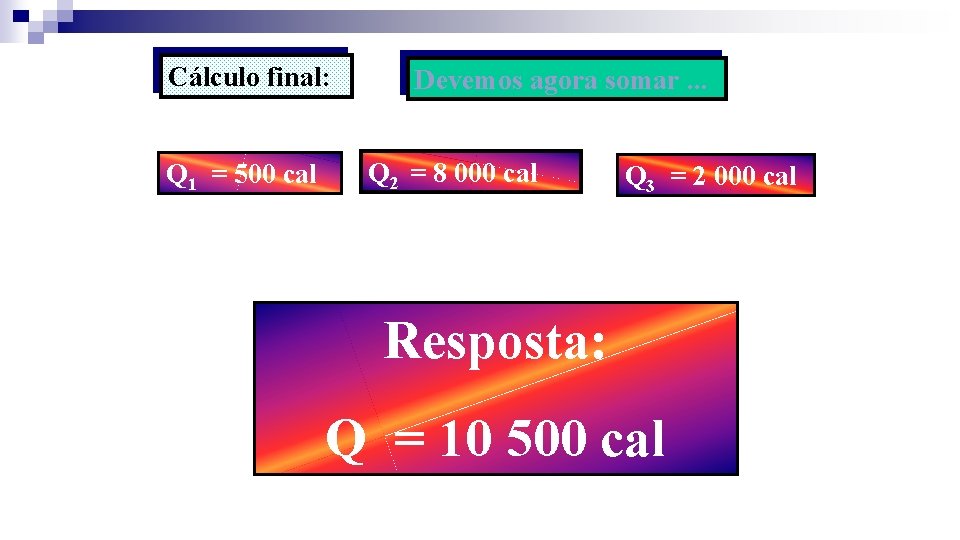
Cálculo final: Q 1 = 500 cal Devemos agora somar. . . Q 2 = 8 000 cal Q 3 = 2 000 cal Resposta: Q = 10 500 cal

Capacidade Térmica Razão entre a quantidade de calor que o corpo troca (ganhando ou perdendo) e a variação de temperatura que ele sofre nesta troca. Unidade : cal / °C ou J / K

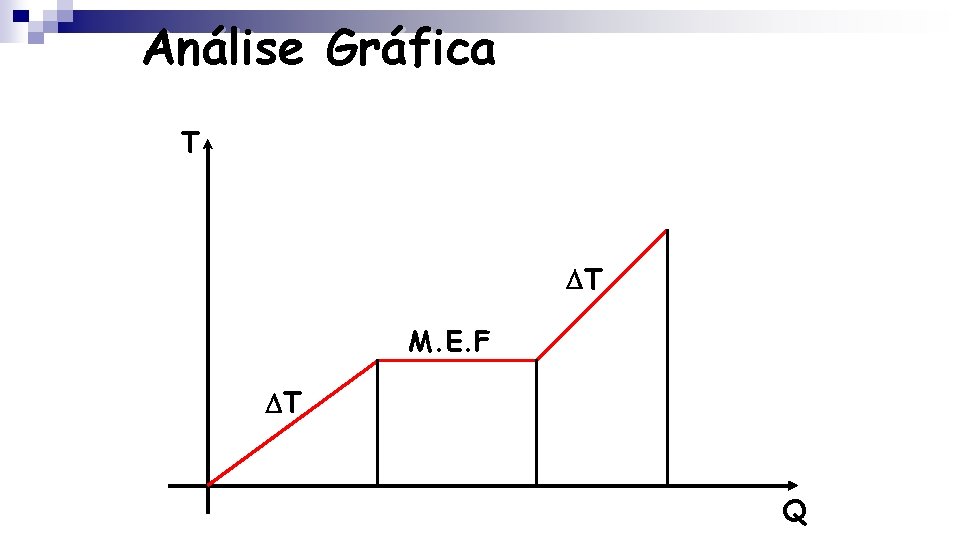
Análise Gráfica T T M. E. F T Q

19) Quando dois corpos de tamanhos diferentes estão em contato e em equilíbrio térmico, e ambos isolados do meio ambiente, pode-se dizer que: a) o corpo maior é o mais quente. b) o corpo menor é o mais quente. c) não há troca de calor entre os corpos. d) o corpo maior cede calor para o corpo menor. e) o corpo menor cede calor para o corpo maior.

20) Quando uma enfermeira coloca um termômetro clínico de mercúrio sob a língua de um paciente, por exemplo, ela sempre aguarda algum tempo antes fazer a sua leitura. Esse intervalo de tempo é necessário a) para que o termômetro entre em equilíbrio térmico com o corpo do paciente. b) para que o mercúrio, que é muito pesado, possa subir pelo tubo capilar. c) para que o mercúrio passe pelo estrangulamento do tubo capilar. d) devido à diferença entre os valores do calor específico do mercúrio e do corpo humano. e) porque o coeficiente de dilatação do vidro é diferente do coeficiente de dilatação do mercúrio.

21

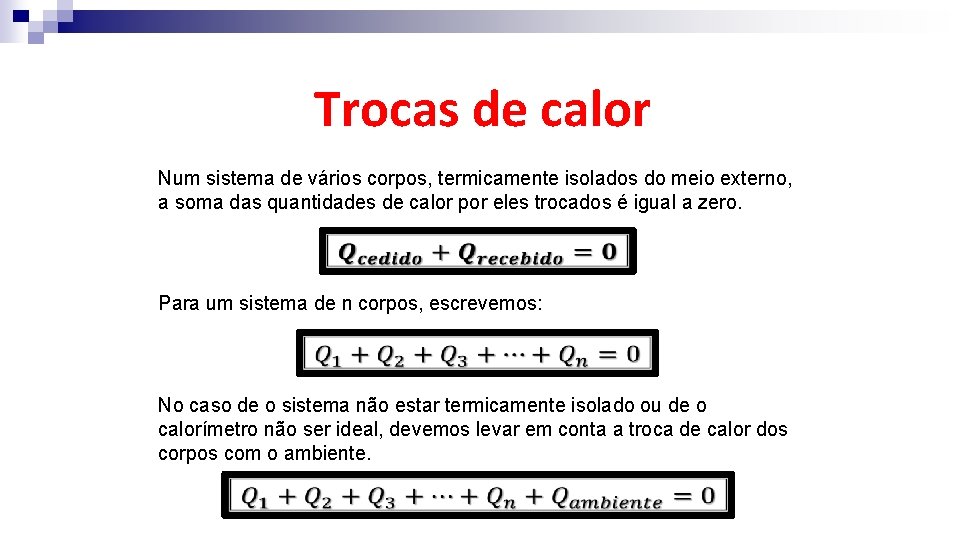
Trocas de calor Num sistema de vários corpos, termicamente isolados do meio externo, a soma das quantidades de calor por eles trocados é igual a zero. Para um sistema de n corpos, escrevemos: No caso de o sistema não estar termicamente isolado ou de o calorímetro não ser ideal, devemos levar em conta a troca de calor dos corpos com o ambiente.

22 - Um recipiente termicamente isolado contém 500 g de água na qual se mergulha uma barra metálica homogênea de 250 g. A temperatura inicial da água é 25, 0°C e a da barra 80, 0°C. Considerando o calor específico da água igual a 1, 00 cal/g. °C, o do metal igual a 0, 056 cal/g. °C e desprezando a capacidade térmica do recipiente, determine a temperatura do equilíbrio térmico.

23 - Um bloco de massa 2, 0 kg, ao receber toda energia térmica liberada por 1000 g de água que diminuem a sua temperatura de 1°C, sofre um acréscimo de temperatura de 10°C. O calor específico do bloco, em cal/g. °C, é: (Adote: cágua: 1, 0 cal/g. °C) a) 0, 2 b) 0, 1 c) 0, 15 d) 0, 05 e) 0, 01

Resolução Sabemos que: Substituindo os valores, obtemos: Como todo calor liberado pela água vai ser aproveitado para aquecer o bloco, temos que: Resposta: d)

24 -Um frasco contém 20 g de água a 0°C. Em seu interior é colocado um objeto de 50 g de alumínio a 80°C. Os calores específicos da água e do alumínio são respectivamente 1, 0 cal/g°C e 0, 10 cal/g°C. Supondo não haver troca de calor com o frasco e com o meio ambiente, a temperatura de equilíbrio dessa mistura será: a) 60°C b) 16°C c) 40°C d) 32°C e) 10°C

Resolução Substituindo os valores, obtemos: Sabemos que: Como não vai haver troca de calor com o meio externo, temos que: Resposta: b)

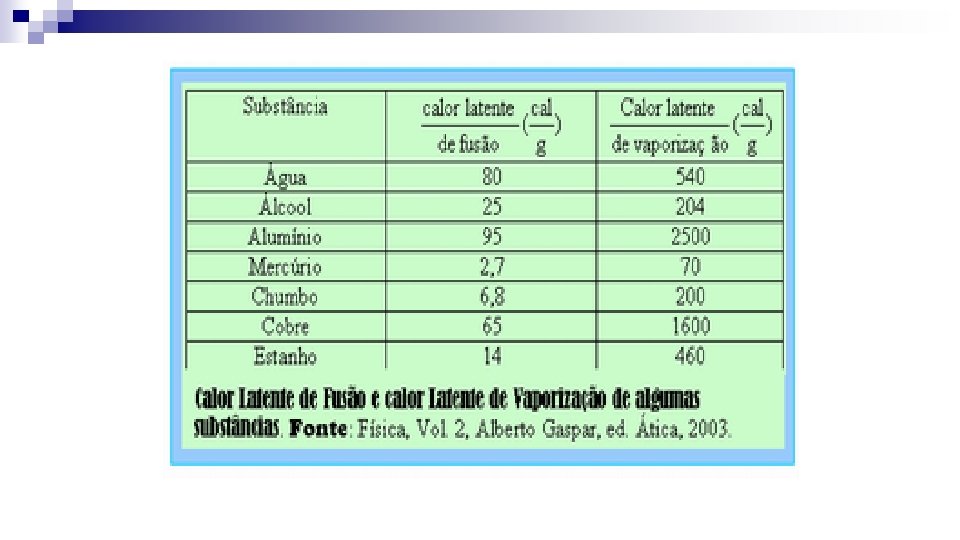
Calor latente O calor latente, de uma mudança de estado, é a quantidade de calor que a substância recebe ou cede, por unidade de massa, durante a transformação, mantendo-se constante a temperatura, desde que a pressão não se altere. Matematicamente, podemos expressá-lo por: Sendo: Q = quantidade total de calor latente trocada no processo ¨ m = massa do corpo ¨ L = calor latente de mudança. ¨

Mudança de fase Quando alteramos as condições físicas de pressão e temperatura, podemos alterar o estado de agregação da matéria. Por ora, trataremos da mudança de fase sob pressão constante, variando somente a temperatura. Processos de mudança: ¨ ¨ ¨ Fusão: passagem de sólido para líquido; Solidificação: passagem de líquido para sólido; Vaporização: passagem de líquido para vapor; Condensação: passagem de vapor para líquido; Sublimação: passagem de sólido para vapor ou vapor para sólido, processo também conhecido como cristalização.

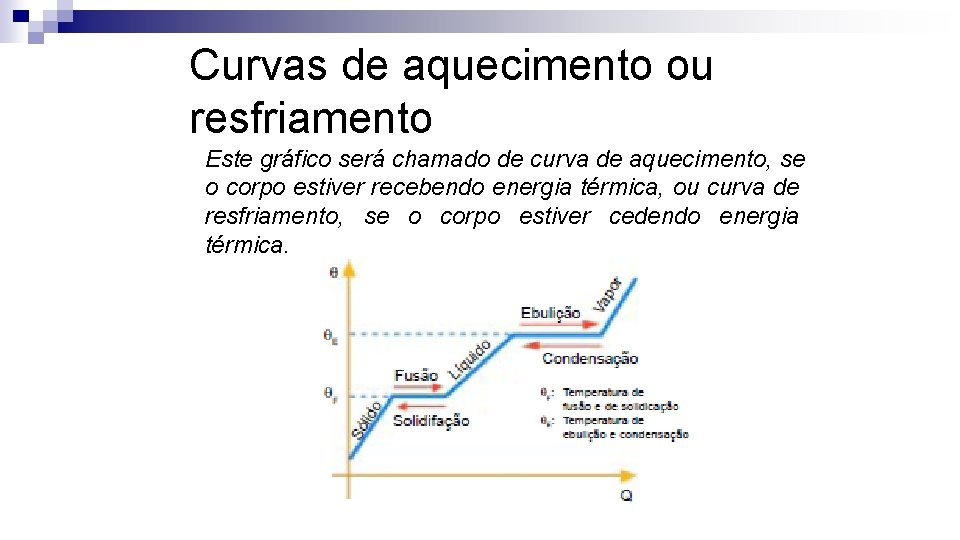
Curvas de aquecimento ou resfriamento Este gráfico será chamado de curva de aquecimento, se o corpo estiver recebendo energia térmica, ou curva de resfriamento, se o corpo estiver cedendo energia térmica.

25 -Calcule a quantidade de calor necessária para transformar 100 g de gelo a - 10 o C em água a 20 o C Dados: calor específico do gelo = 0, 5 cal / g o. C calor latente de fusão do gelo = 80 cal / g calor específico da água = 1 cal / g o. C 1 a parte: Solução: O gelo se encontra numa temperatura abaixo do ponto de fusão, neste caso será aquecido de - 10 o C até o seu ponto de fusão (0 o C): Q =m. c. t Q 1 = m. c. t Q 1 = 100. 0, 5. (0 - (-10)) Q 1 = 50. (10 ) Q 1 = 500 cal

2 a parte: Chegando a 0 o. C, o gelo agora se encontra na temperatura do ponto de fusão, neste caso sofrerá mudança de fase: Q = m. L Q 2 = 100. 80 Q 2 = 8 000 cal 3 a parte: O gelo agora já se transformou em água e esta água será aquecida de 0 o C até 20 o C: Q =m. c. t Q 3 = m. c. t Q 3 = 100. 1. (20 - 0) Q 3 = 100. 20 Q 3 = 2 000 cal

Cálculo final: Q 1 = 500 cal Devemos agora somar. . . Q 2 = 8 000 cal Q 3 = 2 000 cal Resposta: Q = 10 500 cal