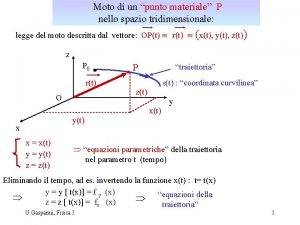
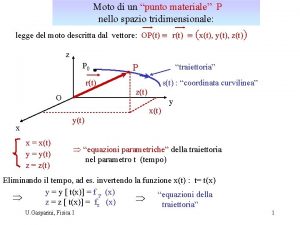
Moto nello spazio tridimensionale La localizzazione spaziotemporale di

Moto nello spazio tridimensionale La localizzazione spazio-temporale di un ‘evento’ (es. : il punto materiale P si trova in un certo posto ad un dato istante con una data velocità) richiede : - la definizione di un sistema di coordinate definizione di un punto arbitrario “origine” O e di un sistema di assi rispetto ai quali misurare gli spostamenti (distanze e/o angoli) Nella “Meccanica classica” (“newtoniana”), le proprietà geometriche dello spazio sono le stesse (quelle della “geometria euclidea”) in ogni punto dello spazio - la definizione di un modo di misurare il tempo : in Meccanica classica, è un parametro assoluto che ordina la successione degli eventi in un dato punto nella stessa maniera in ogni punto dello spazio ed in tutti i sistemi di coordinate (anche in moto relativo uno rispetto all’altro) : esso è misurato da “orologi” (sistemi fisici che esibiscono fenomeni periodici) il cui procedere è assunto essere lo stesso in tutti i punti dello spazio e indipendentemente dal loro stato di moto Þ assolutezza del concetto di “contemporaneità” di eventi in punti diversi dello spazio U. Gasparini, Fisica I 1

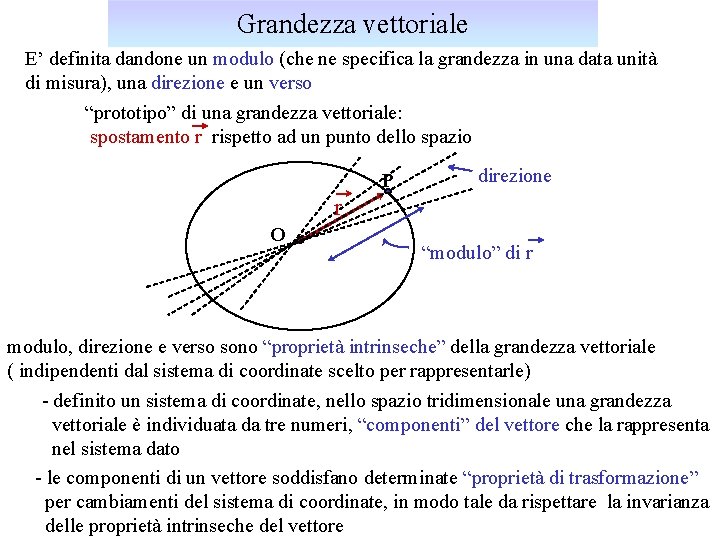
Grandezza vettoriale E’ definita dandone un modulo (che ne specifica la grandezza in una data unità di misura), una direzione e un verso “prototipo” di una grandezza vettoriale: spostamento r rispetto ad un punto dello spazio P direzione r O “modulo” di r modulo, direzione e verso sono “proprietà intrinseche” della grandezza vettoriale ( indipendenti dal sistema di coordinate scelto per rappresentarle) - definito un sistema di coordinate, nello spazio tridimensionale una grandezza vettoriale è individuata da tre numeri, “componenti” del vettore che la rappresenta nel sistema dato - le componenti di un vettore soddisfano determinate “proprietà di trasformazione” per cambiamenti del sistema di coordinate, in modo tale da rispettare la invarianza delle proprietà intrinseche del vettore

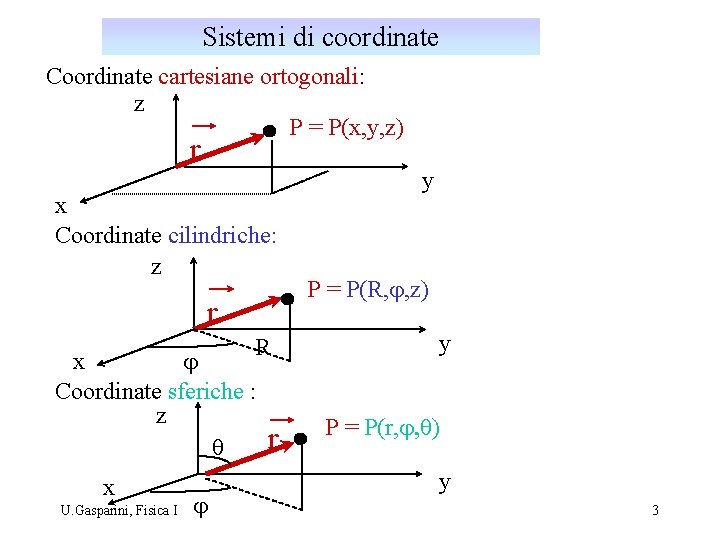
Sistemi di coordinate Coordinate cartesiane ortogonali: z P = P(x, y, z) r x Coordinate cilindriche: z r R x j Coordinate sferiche : z q x U. Gasparini, Fisica I j r y P = P(R, j, z) y P = P(r, j, q) y 3

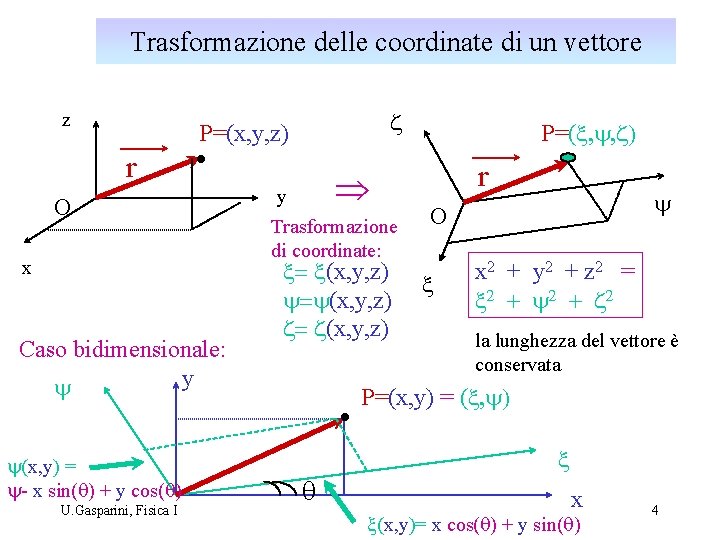
Trasformazione delle coordinate di un vettore z z P=(x, y, z) r O x Caso bidimensionale: y y y(x, y) = y- x sin(q) + y cos(q) U. Gasparini, Fisica I Þ y Trasformazione di coordinate: x= x(x, y, z) y=y(x, y, z) z= z(x, y, z) P=(x, y, z) r y O x x 2 + y 2 + z 2 = x 2 + y 2 + z 2 la lunghezza del vettore è conservata P=(x, y) = (x, y) q x x x(x, y)= x cos(q) + y sin(q) 4

Rotazione del sistema di coordinate in un piano: y P r =OP J x O La trasformazione : (x, y) Û (x, y ) mantiene invariante l’espressione che rappresenta il modulo del vettore r : ½OP½ è una quantità scalare

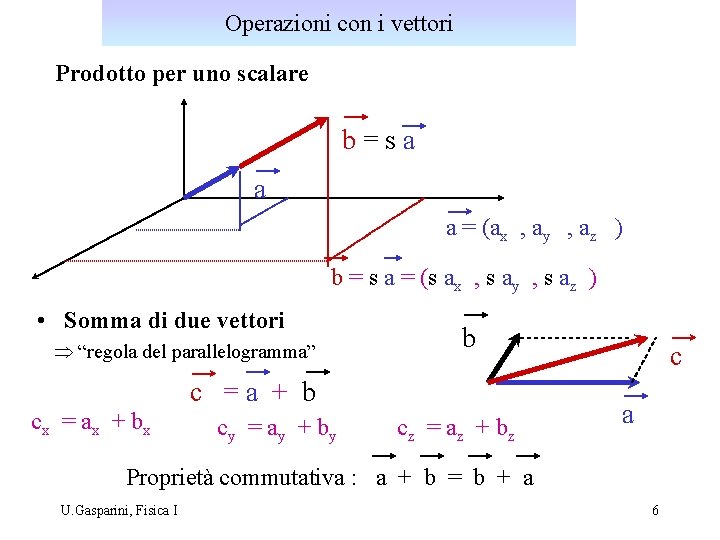
Operazioni con i vettori Prodotto per uno scalare b=sa a a = (ax , ay , az ) b = s a = (s ax , s ay , s az ) • Somma di due vettori Þ “regola del parallelogramma” b c =a + b cx = ax + bx cy = a y + by cz = az + bz c a Proprietà commutativa : a + b = b + a U. Gasparini, Fisica I 6

Versori • “Versore” u : vettore di modulo unitario: • Versori degli assi coordinati : z u x = (1, 0, 0) u y = (0, 1, 0) u z = (0, 0, 1) uz ux y uy x • Espressione di un vettore in funzione dei versori degli assi coordinati : a = ayux+ ayuy + azuz z a axux U. Gasparini, Fisica I x azuz y ayuy 7

Prodotto scalare di due vettori E’ una quantità scalare: qab b a in particolare: Vale la proprietà distributiva: infatti: qb b bcosqb c qc qd a c cosqc dcosqd = bcosqb + c cosqc U. Gasparini, Fisica I 8

Prodotto scalare in coordinate cartesiane Dalle proprietà precedenti, è facile ricavare l’ espressione del prodotto scalare in funzione delle coordinate cartesiane dei vettori : =1 U. Gasparini, Fisica I =0 9

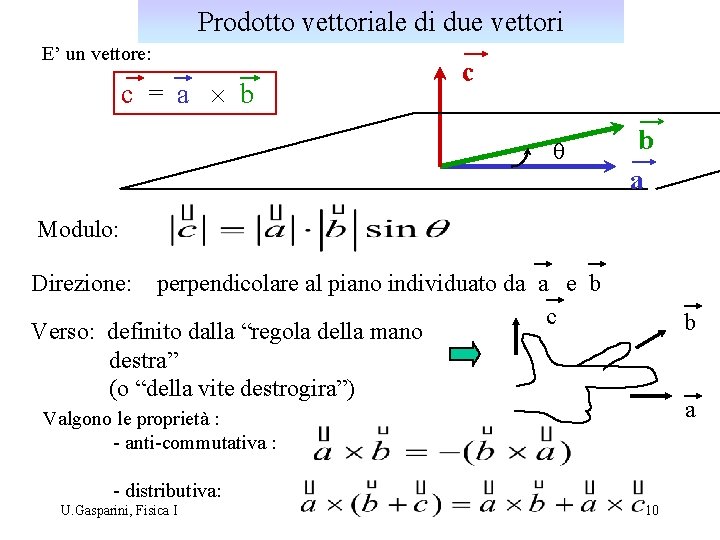
Prodotto vettoriale di due vettori E’ un vettore: c = a b c q b a Modulo: Direzione: perpendicolare al piano individuato da a e b c Verso: definito dalla “regola della mano destra” (o “della vite destrogira”) b a Valgono le proprietà : - anti-commutativa : - distributiva: U. Gasparini, Fisica I 10

Prodotto vettoriale in coordinate cartesiane uz = ux uy Þ ux p/2 uy Espressione del prodotto vettoriale in funzione delle coordinate cartesiane : =0 = ax by ( ux uy ) = ax by uz In forma “matriciale”: U. Gasparini, Fisica I 11