Moto di un punto materiale P nello spazio

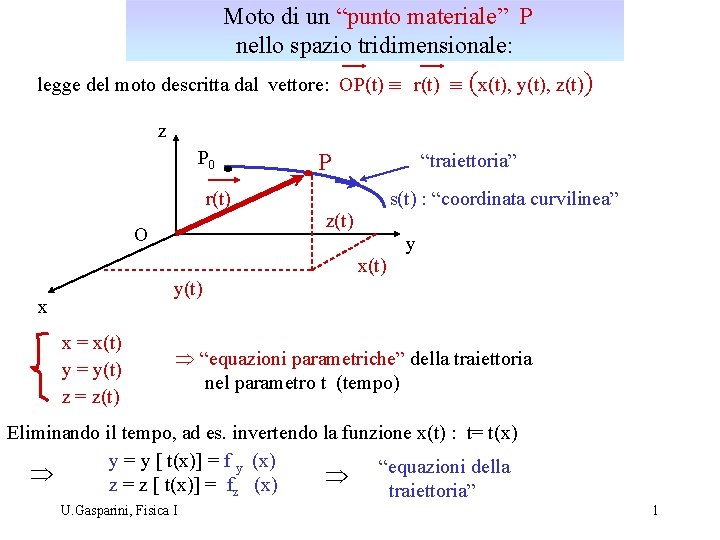
Moto di un “punto materiale” P nello spazio tridimensionale: legge del moto descritta dal vettore: OP(t) º r(t) º (x(t), y(t), z(t)) z P 0 P “traiettoria” r(t) s(t) : “coordinata curvilinea” z(t) O y x(t) y(t) x x = x(t) y = y(t) z = z(t) Þ “equazioni parametriche” della traiettoria nel parametro t (tempo) Eliminando il tempo, ad es. invertendo la funzione x(t) : t= t(x) y = y [ t(x)] = f y (x) “equazioni della Þ Þ z = z [ t(x)] = fz (x) traiettoria” U. Gasparini, Fisica I 1

Vettore velocità : r(t) Dr r (t+ Dt) O La velocità é un vettore tangente alla traiettoria : P(t + Dt) s(t) P(t) dr Dr Dr ® dr = ds u. T Dt ® 0 U. Gasparini, Fisica I versore tangente 2 velocità scalare

Componenti cartesiane del vettore velocità Infatti: Se è nota la funzione (vettoriale) velocità, la legge del moto r(t) si ottiene per integrazione : Þ Þ Û U. Gasparini, Fisica I 3

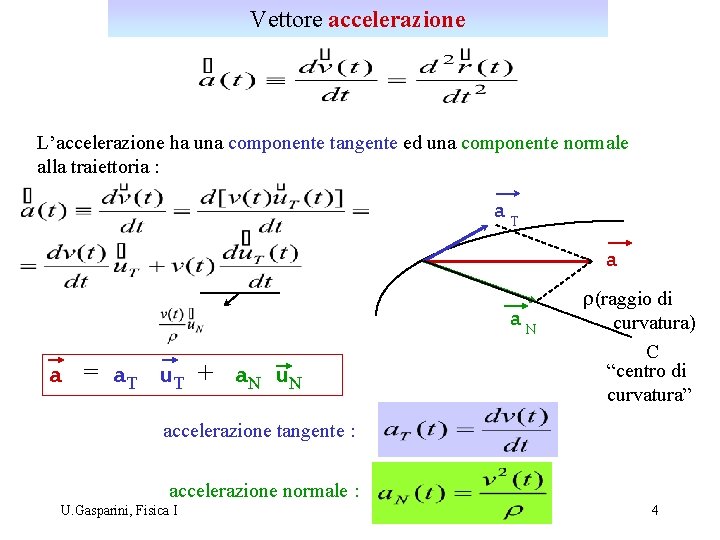
Vettore accelerazione L’accelerazione ha una componente tangente ed una componente normale alla traiettoria : a. T a a. N a = a. T u. T + a. N u. N r(raggio di curvatura) C “centro di curvatura” accelerazione tangente : accelerazione normale : U. Gasparini, Fisica I 4

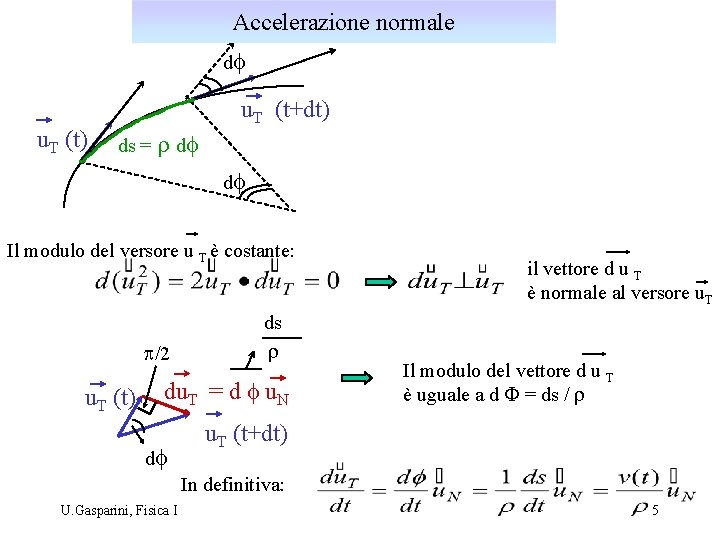
Accelerazione normale df u. T (t) u. T (t+dt) ds = r df df Il modulo del versore u T è costante: p/2 u. T (t) ds r du. T = d f u. N df il vettore d u T è normale al versore u. T Il modulo del vettore d u T è uguale a d F = ds / r u. T (t+dt) In definitiva: U. Gasparini, Fisica I 5

Componenti cartesiane dell’ accelerazione Infatti: U. Gasparini, Fisica I 6

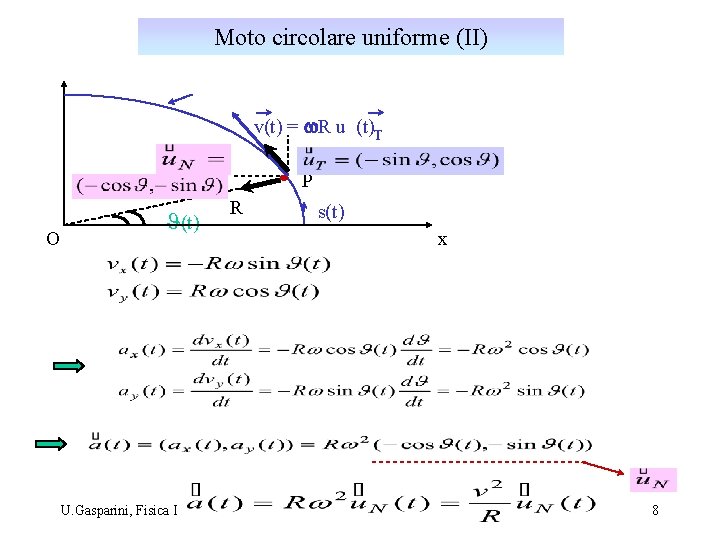
coordinata curvilinea s(t)=RJ (t) Esempio: moto circolare uniforme velocità con modulo costante: y traiettoria v(t) = w. R u (t)T P R O J(t) “velocità angolare”: s(t)=R J (t) x Þ Þ Þ U. Gasparini, Fisica I 7

Moto circolare uniforme (II) v(t) = w. R u (t)T P O J(t) U. Gasparini, Fisica I R s(t) x 8

Integrazione della velocità Invertendo la relazione che definisce l’accelerazione e integrando : Þ Þ Û U. Gasparini, Fisica I 9

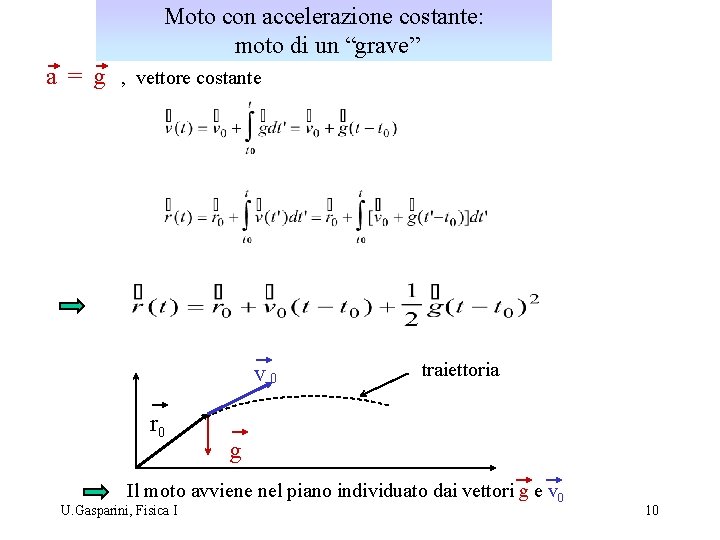
Moto con accelerazione costante: moto di un “grave” a = g , vettore costante v 0 r 0 traiettoria g Il moto avviene nel piano individuato dai vettori g e v 0 U. Gasparini, Fisica I 10

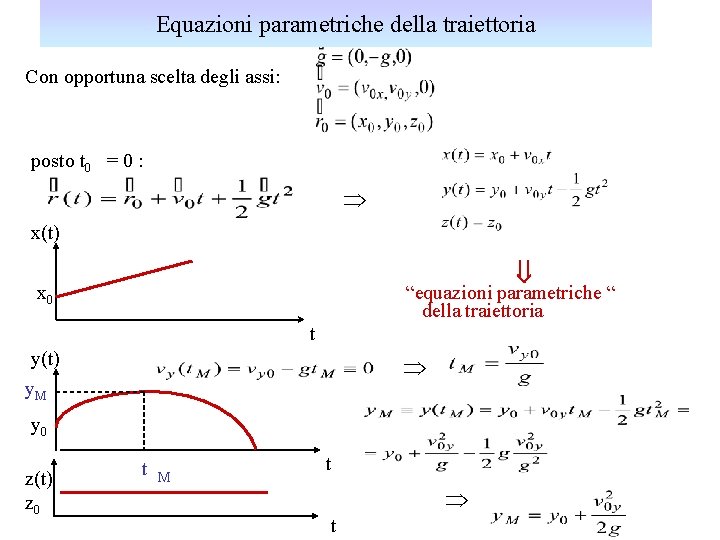
Equazioni parametriche della traiettoria Con opportuna scelta degli assi: posto t 0 = 0 : Þ x(t) ß x 0 “equazioni parametriche “ della traiettoria t y(t) y. M Þ y 0 z(t) z 0 t M t Þ t

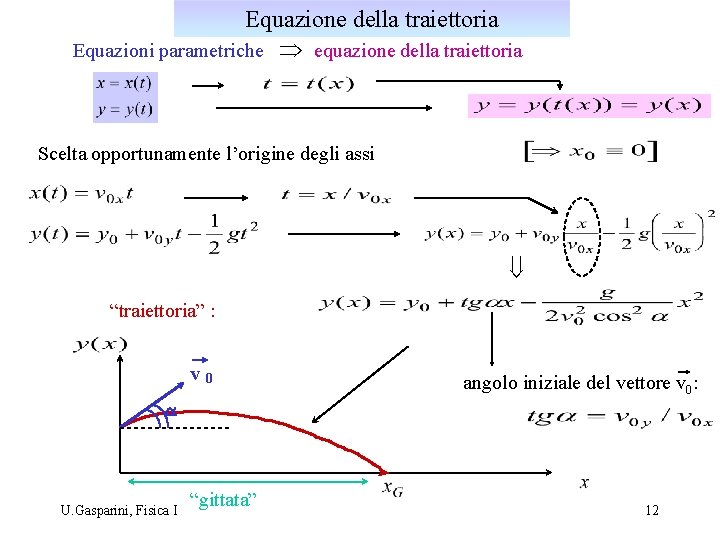
Equazione della traiettoria Equazioni parametriche Þ equazione della traiettoria Scelta opportunamente l’origine degli assi ß “traiettoria” : v 0 angolo iniziale del vettore v 0: a U. Gasparini, Fisica I “gittata” 12

Gittata nel moto di un grave Þ Per Þ Þ “gittata” : Fissato il modulo di v 0 , la gittata è funzione dell’inclinazione iniziale a ; gittata massima : 0. U. Gasparini, Fisica I 13 a

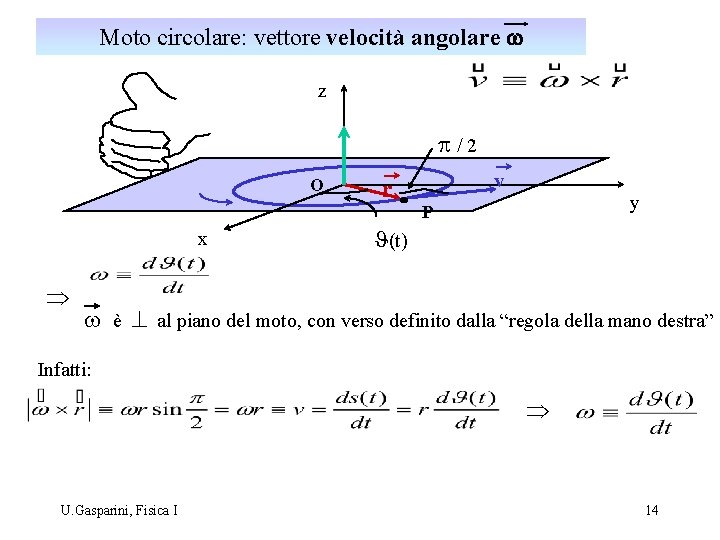
Moto circolare: vettore velocità angolare w z p/2 O x Þ r v y P J(t) w è ^ al piano del moto, con verso definito dalla “regola della mano destra” Infatti: Þ U. Gasparini, Fisica I 14

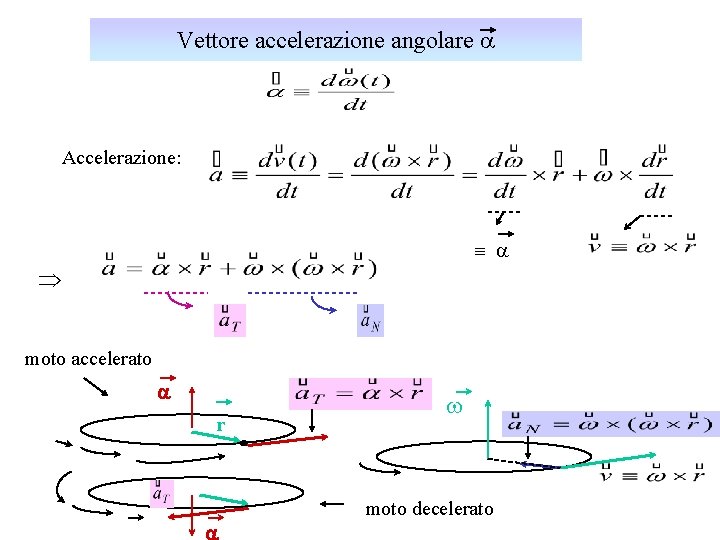
Vettore accelerazione angolare a Accelerazione: º a Þ moto accelerato a r w moto decelerato a

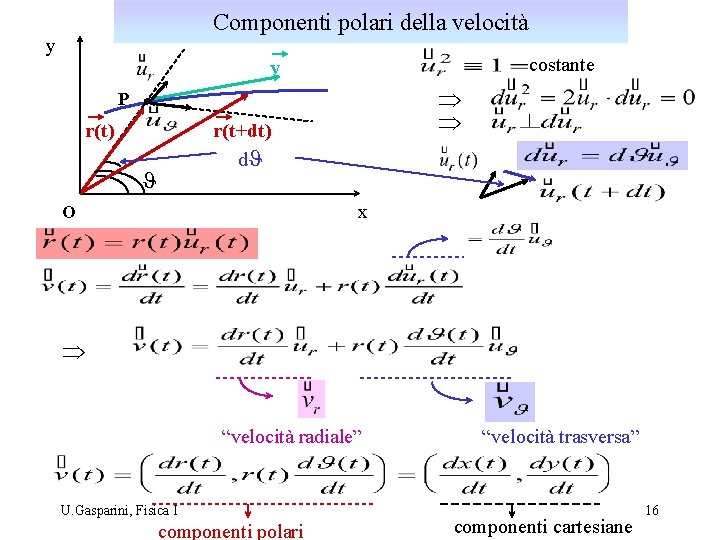
Componenti polari della velocità y costante v Þ Þ P r(t) r(t+dt) d. J J x O Þ “velocità radiale” U. Gasparini, Fisica I componenti polari “velocità trasversa” componenti cartesiane 16

Componenti polari dell’ accelerazione Þ “accelerazione radiale” In un moto circolare ( r = costante) : “accelerazione trasversa”

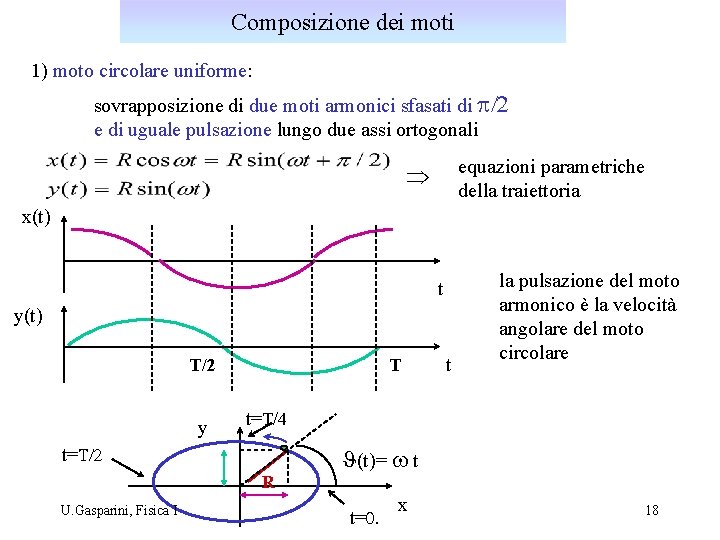
Composizione dei moti 1) moto circolare uniforme: sovrapposizione di due moti armonici sfasati di p/2 e di uguale pulsazione lungo due assi ortogonali equazioni parametriche della traiettoria Þ x(t) t y(t) T/2 y T t=T/4 t=T/2 R U. Gasparini, Fisica I t la pulsazione del moto armonico è la velocità angolare del moto circolare J(t)= w t t=0. x 18

Esempi di composizione dei moti 2) moto di una “cicloide” composizione di un moto circolare uniforme di raggio R con velocità angolare w e di un moto traslatorio con velocità v = w. R nel piano del moto circolare equazioni parametriche della traiettoria y C moto del punto periferico di una ruota in moto con velocità costante P v = w. R x 3) moto “elicoidale” composizione di un moto circolare e di un moto traslatorio con velocità v perpendicolare al piano del moto circolare z U. Gasparini, Fisica I y x 19