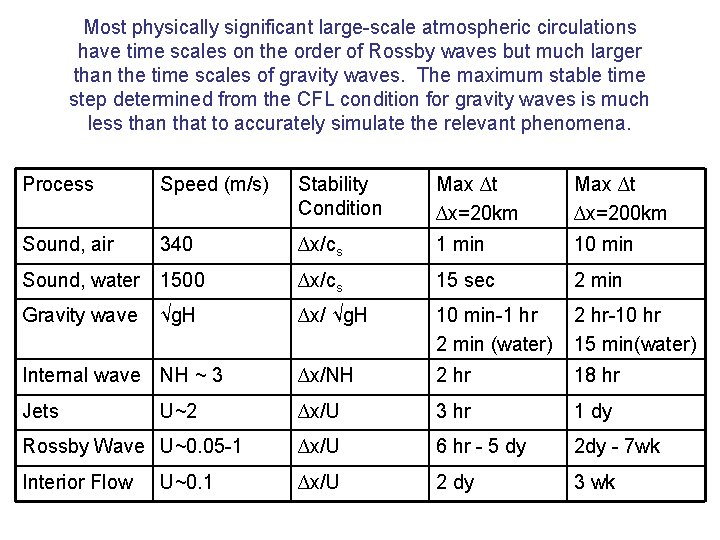
Most physically significant largescale atmospheric circulations have time














- Slides: 15



Most physically significant large-scale atmospheric circulations have time scales on the order of Rossby waves but much larger than the time scales of gravity waves. The maximum stable time step determined from the CFL condition for gravity waves is much less than that to accurately simulate the relevant phenomena. Process Speed (m/s) Stability Condition Max ∆t ∆x=20 km Max ∆t ∆x=200 km Sound, air 340 ∆x/cs 1 min 10 min Sound, water 1500 ∆x/cs 15 sec 2 min Gravity wave √g. H ∆x/ √g. H 10 min-1 hr 2 min (water) 2 hr-10 hr 15 min(water) Internal wave NH ~ 3 ∆x/NH 2 hr 18 hr Jets ∆x/U 3 hr 1 dy Rossby Wave U~0. 05 -1 ∆x/U 6 hr - 5 dy 2 dy - 7 wk Interior Flow ∆x/U 2 dy 3 wk U~2 U~0. 1

Ways to Circumvent Time Constraints • Approximate the full governing equations with a “filtered” set of equations. – Primitive Equations – Euler Equations – Vorticity Eqns with Geostrophic Approx. • Use numerical techniques to stabilize the fastmoving waves. Generally, accuracy of the fast waves is sacrificed for efficiency.

Implicit Schemes Discretize: Center the time-derivative and choose level for RHS. Explicit: The same equation with 2 x the time step gives the more common form of an explicit scheme. Implicit: Most often use some combination of the two schemes => Semi-Implicit

Example: Diffusion Assume that the diffusion coefficient is constant. Explicit: von Neumann => Stability Constraint =>

Example: Diffusion Implicit: This system can be solved by inverting the tridiagonal matrix. Using the boundary conditions to solve backwards in time! Often fully implicit schemes are too difficult to invert efficiently. von Neumann Stability => => Unconditionally stable A 1 for all ∆t>0. => Only first order accurate.

Example: Diffusion Semi-Implicit Scheme: A combination of the implicit and explicit. Crank-Nicholson Scheme von Neumann Stability => => Unconditionally Stable AND accurate.

Notes on Using Implicit Schemes • Higher order implicit schemes are not necessarily more stable than the related explicit methods. – Example: the 3 rd and 4 th order Adams-Moulton schemes (Backward and Trapezoid are the 1 st and 2 nd order of this family) generally amplify solutions for any choice of time step. • Generally, only use implicit schemes for those terms that are crucial to fast waves. Use explicit methods on all other terms.

Example: Shallow Water Equations and Gravity Waves


Split into Baroclinic and Barotropic modes. Rossby wave = Low Frequency Gravity wave = High Frequency

Mixed Schemes Trapezoid method. Stable when the mean flow, U, < gravity wave speed, the fluid depth, H, > the wave perturbations and the CFL condition for the Rossby wave is satisfied. These conditions are not always satisfied in the polar regions of the Earth’s atmosphere. Here, the averaging can occur in a couple different ways: The trapezoid method as above. The longer time step can be subdivided into M smaller steps ∆t/M, iterated only for the gravity wave term and then averaged over the longer time step. Note: the gravity wave term is slowed down for this calculation.


Le. Veque: Finite Difference Methods for Ordinary and Partial Differential Equations; SIAM, 2007.
 Rectangular prism vertices
Rectangular prism vertices Bitwise operators
Bitwise operators Most significant
Most significant A physically educated person
A physically educated person 3 modifiers of human acts
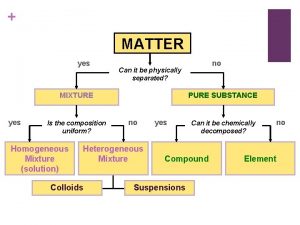
3 modifiers of human acts Matter can it be physically separated
Matter can it be physically separated Physically compromised
Physically compromised Output devices for physically challenged users
Output devices for physically challenged users Operators in quantum mechanics
Operators in quantum mechanics Virtual memory
Virtual memory Vinput leah
Vinput leah Corporate athlete personal development plan
Corporate athlete personal development plan Mentally spiritually physically emotionally
Mentally spiritually physically emotionally What do you mean by physical diversity
What do you mean by physical diversity Physically based animation
Physically based animation Why are jekyll and lanyon no longer friends
Why are jekyll and lanyon no longer friends