Metode Komputasi 3 Metode Gradient untuk masalah optimasi

Metode Komputasi 3 Metode Gradient untuk masalah optimasi: Regresi linear dan non linear

Jumlah Penduduk Indonesia Tahun 2000 2001 2002 2003 2004 2005 Jumlah (dalam ribuan) 205, 132. 00 207, 927. 50 210, 736. 30 213, 550. 50 216, 381. 60 219, 204. 70 Sumber: datastatistik-indonesia. com Bila jumlah penduduk diasumsikan bertambah secara linear terhadap waktu (tahun), maka jumlah penduduk dapat diprediksi dengan menggunakan persamaan linear Y = 1 x + 0, x menyatakan tahun setelah tahun 2000 Jumlah Bagaimana menaksir parameter 1 dan 0? tahun Definisi: Jarak vertikal antara garis Y = 1 x + 0 ke titik Pi(xi, yi) Ji = |yi – ( 1 xi + 0)| = |yi – 1 xi – 0 | Garis Y = 1 x + 0 dipilih sehingga jumlah kuadrat jarak vertikal terkecil

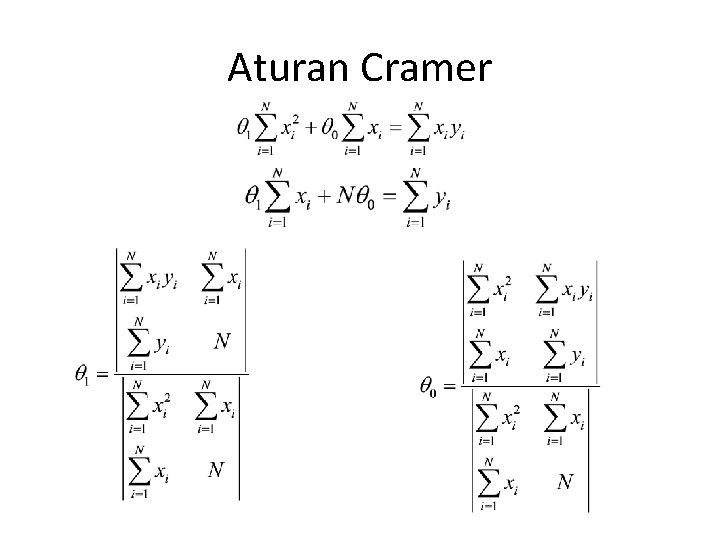
Garis Jumlah Kuadrat Terkecil Garis kuadrat terkecil Y = 1 x + 0 untuk himpunan titik (x 1, y 1), (x 2, y 2), …, (xn, yn) dapat diperoleh dari masalah peminimuman Bagaimana menentukan nilai 1 dan 0 yang memenuhi masalah optimasi? Berdasarkan kalkulus, syarat perlu agar J( 1, 0) mencapai minimum Atau Maka, titik kritis Dengan asumsi J fungsi yang terdifferensialkan

Aturan Cramer

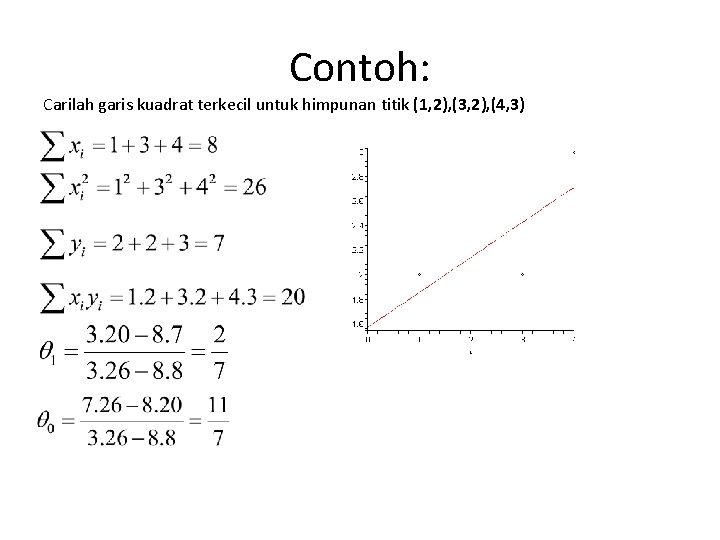
Contoh: Carilah garis kuadrat terkecil untuk himpunan titik (1, 2), (3, 2), (4, 3)

Nonlinear Fitting Diberikan sekumpulan data: (x 1, y 1), (x 2, y 2), …, (xn, yn) Jika hubungan antara Y dan X diasumsikan Y = e X ln. Y = ln + X Maka Y = ln. Y 0 = ln 1 = Contoh: Data set: (1, 2), (2, 4), (3, 9) Y=(2, 4, 9) Y = ln(2, 4, 9) XY = … dst

Nonlinear Fitting Diberikan sekumpulan data: (x 1, y 1), (x 2, y 2), …, (xn, yn) Jika hubungan antara Y dan X diasumsikan Y = x ln. Y = ln + ln. X Maka Y = ln. Y X = ln. X 0 = ln 1 = Jika diasumsikan

Grad. Descent utk Reg. Linear ekivalen dengan Berangkat dari ( 1(0), 0(0)) , arah pergerakan yang memberikan penurunan paling besar : - J ( 1(0), 0(0)) Sehingga, iterasi ( 1(k+1), 0(k+1))=( 1(k), 0(k)) - J ( 1(k), 0(k)) konvergen ke nilai minimum ‘lokal’ dari J untuk suatu nilai yang cukup kecil. Ulangi proses sampai konvergen 1 = 1 + (yi- 1 xi - 0)xi 0 = 0 + (yi- 1 xi - 0)

Grad. Descent utk Reg. Linear (Perumuman) Berangkat dari arah pergerakan yang memberikan penurunan paling besar : - J ( (0)) Sehingga, iterasi (k+1) = (k) - J (k), konvergen ke nilai minimum ‘lokal’ dari J untuk suatu nilai yang cukup kecil. Ulangi proses sampai konvergen k = k + (yi- Txi)xik, k=1, 2, …, M Xi 0 = 1 untuk semua i=1, 2, …, N

Logistic Fitting Diberikan sekumpulan data: (x 1, y 1), (x 2, y 2), …, (xn, yn) Jika Y bernilai biner {0, 1} dan diasumsikan Gradien Descent: 1= 1 - R/ 1 0= 0 - R/ 0 dengan Z = 0 + 1 X Maka nilai 0, 1 diperoleh Student id Outcome Quantity of Study Hours 1 0 3 2 1 34 3 0 17 4 0 6 5 0 12 6 1 15 7 1 26 8 1 29 9 0 14 10 1 58 11 0 2

Logistic Fitting (Generalization) Diberikan sekumpulan data: (x 1, y 1), (x 2, y 2), …, (xn, yn) Jika Y bernilai biner {0, 1} dan diasumsikan dengan Z = TX Gradien Descent: k= k- R/ k