Matrices MSU CSE 260 31003 MSU CSE 260

Outline • Introduction • Matrix Arithmetic: – Sum, Product • Transposes and Powers of

Introduction Definition A matrix is a rectangular array of numbers. element in ith row,

Matrix Equality • Definition Let A and B be two matrices. A=B if they

Matrix Addition, Subtraction Let A = aij , B = bij be m n

Matrix Multiplication Let A be a m k matrix, and B be a k

Matching Dimensions To multiply two matrices, inner numbers must match: Otherwise, 2 3 3

Multiplicative Properties Note that just because AB is defined, BA may not be. Example

Efficiency of Multiplication 2 3 3 4 a 11 b 12 + a 12

Best Order? Let A be a 20 30 matrix, B 30 40, C 40

Identity Matrix The identity matrix has 1’s down the diagonal, e. g. : For

Inverse Matrix Let A and B be n n matrices. If AB=BA=In then B

Use of Inverse to Solve Equations Please note that a-1 j is NOT necessarily

Transposes of Matrices Flip across diagonal Transposes are used frequently in various algorithms. 3/10/03

Symmetric Matrix A is called symmetric. is symmetric. Note, for A to be symmetric,

Examples 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 16

Power Matrix • For a n n square matrix A, the power matrix is

Zero-one Matrices • All entries are 0 or 1. • Operations are and .

Boolean Operations Terminology is from Boolean Algebra. Think “join” is “put together”, like union,

Boolean Product (Should be a ‘dot’) Since this is “or’d”, you can stop when

Boolean Product Properties • In general, A B B A • Example 3/10/03 MSU

Boolean Power • A Boolean power matrix can be defined in exactly the same

Exercise 2. 6 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 23

Slides: 23

Download presentation

Matrices MSU CSE 260 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 1

Outline • Introduction • Matrix Arithmetic: – Sum, Product • Transposes and Powers of Matrices – Identity matrix, Transpose, Symmetric matrices • Zero-one Matrices: – Join, Meet, Boolean product • Exercise 2. 6 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 2

Introduction Definition A matrix is a rectangular array of numbers. element in ith row, jth column m rows Also written as A= aij m n matrix n columns When m=n, A is called a square matrix. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 3

Matrix Equality • Definition Let A and B be two matrices. A=B if they have the same number of rows and columns, and every element at each position in A equals element at corresponding position in B. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 4

Matrix Addition, Subtraction Let A = aij , B = bij be m n matrices. Then: A + B = aij + bij , and A - B = aij - bij 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 5

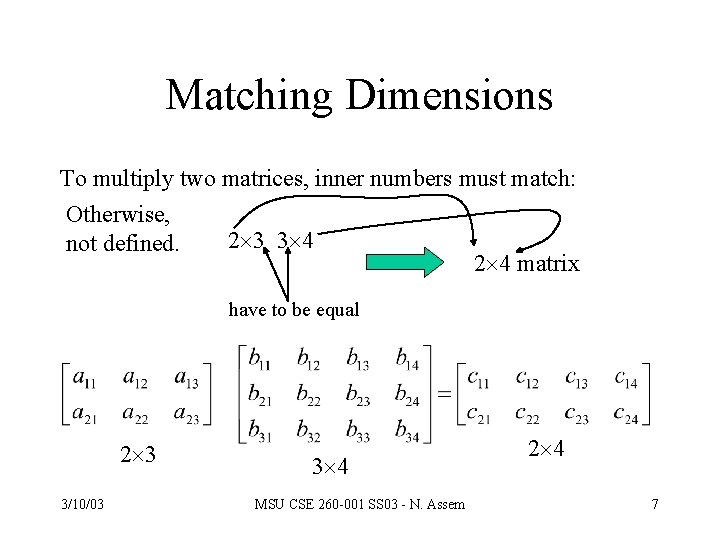
Matrix Multiplication Let A be a m k matrix, and B be a k n matrix, 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 6

Matching Dimensions To multiply two matrices, inner numbers must match: Otherwise, 2 3 3 4 not defined. 2 4 matrix have to be equal 2 3 3/10/03 3 4 MSU CSE 260 -001 SS 03 - N. Assem 2 4 7

Multiplicative Properties Note that just because AB is defined, BA may not be. Example If A is 3 4, B is 4 6, then AB=3 6, but BA is not defined (4 6. 3 4). Even if both AB and BA are defined, they may not have the same size. Even if they do, matrices do not commute. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 8

Efficiency of Multiplication 2 3 3 4 a 11 b 12 + a 12 b 22 + a 13 b 32 = c 12 Takes 3 multiplications, and 2 additions for each element. This has to be done 2 4 (=8) times (since product matrix is 2 4). So 2 4 3 multiplications are needed. • (m k) (k n) matrix product requires m. k. n multiplications. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 9

Best Order? Let A be a 20 30 matrix, B 30 40, C 40 10. (AB)C or A(BC)? (20 30 30 40) 40 10 32000 20 30 (30 40 40 10) 18000 So, A(BC) is best in this case. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 10

Identity Matrix The identity matrix has 1’s down the diagonal, e. g. : For a m n matrix A, Im A = A In m m m n = m n n n 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 11

Inverse Matrix Let A and B be n n matrices. If AB=BA=In then B is called the inverse of A, denoted B=A-1. Not all square matrices are invertible. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 12

Use of Inverse to Solve Equations Please note that a-1 j is NOT necessarily (aj)-1. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 13

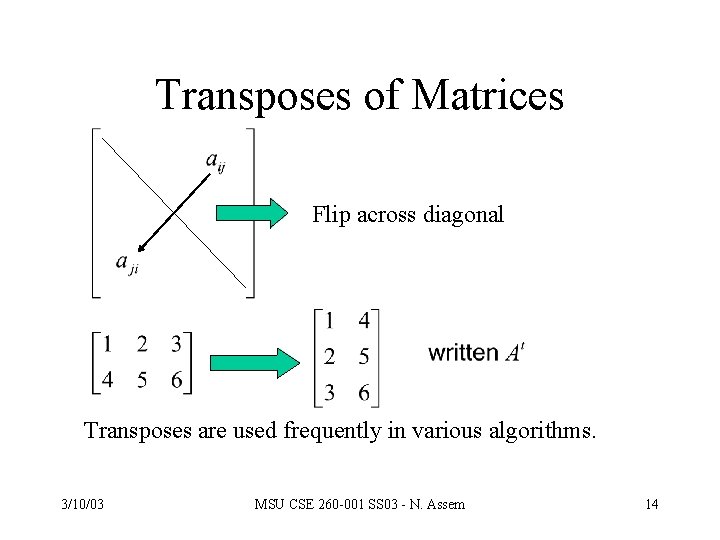
Transposes of Matrices Flip across diagonal Transposes are used frequently in various algorithms. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 14

Symmetric Matrix A is called symmetric. is symmetric. Note, for A to be symmetric, is has to be square. is trivially symmetric. . . 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 15

Examples 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 16

Power Matrix • For a n n square matrix A, the power matrix is defined as: Ar = A A … A r times • A 0 is defined as In. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 17

Zero-one Matrices • All entries are 0 or 1. • Operations are and . • Boolean product is defined using: for multiplication, and for addition. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 18

Boolean Operations Terminology is from Boolean Algebra. Think “join” is “put together”, like union, and “meet” is “where they meet”, or intersect. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 19

Boolean Product (Should be a ‘dot’) Since this is “or’d”, you can stop when you find a ‘ 1’ 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 20

Boolean Product Properties • In general, A B B A • Example 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 21

Boolean Power • A Boolean power matrix can be defined in exactly the same way as a power matrix. For a n n square matrix A, the power matrix is defined as: A[r] = A A … A r times A[0] is defined as In. 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 22

Exercise 2. 6 3/10/03 MSU CSE 260 -001 SS 03 - N. Assem 23