Math Review with Matlab Complex Numbers Complex Number

Math Review with Matlab: Complex Numbers Complex Number Theory S. Awad, Ph. D. M. Corless, M. S. E. E. E. C. E. Department University of Michigan-Dearborn

Complex Numbers: Complex Number Theory n n n General Complex Numbers in Matlab Argand Diagrams Exponential Form Polar Form in Matlab 2

Complex Numbers: Complex Number Theory Representing Complex Numbers n The conventional representation of a complex number z is the sum of a real part x and an imaginary part y Complex n n Real Imaginary i is the imaginary unit where: Conventional representation is also referred to as the rectangular form of a complex number 3

Complex Numbers: Complex Number Theory Functional Notation n n In different applications, the imaginary unit may be represented as i or j and may be placed before or after the imaginary part In functional notation, it is sometimes convenient to write: 4

Complex Numbers: Complex Number Theory Matlab Complex Numbers n n Matlab complex numbers consist of a real portion plus an imaginary portion For example, use Matlab to find the square root of -1 » sqrt(-1) ans = 0 + 1. 0000 i Real Portion = 0 Imaginary Portion = -1 5

Complex Numbers: Complex Number Theory Entering Complex Numbers n n n Both the variables i and j in the Matlab workspace are reserved for representing imaginary numbers Placing i or j after a number defines it as imaginary Example: A complex number with real portion = 1 and imaginary portion = 2 can be entered in two ways: » z = 1+2 i » z = 1+2 j OR z = 1. 0000 + 2. 0000 i 6

Complex Numbers: Complex Number Theory Real and Imag Commands n n The real and imag functions extract the real and imaginary portion of a complex number respectively Example: » z 1= 2+4 i z 1 = 2. 0000 + 4. 0000 i » z 1_re = real(z 1) z 1_re = 2 » z 1_im = imag(z 1) z 1_imag = 4 7

Complex Numbers: Complex Number Theory Argand Diagram n n n A complex number can be represented as a Point P(x, y) in the xy-plane (Cartesian plane) This representation is called an Argand Diagram The xy-plane is often referred to as the Complex Plane or the z-plane n Ordered Pair Notation 8

Complex Numbers: Complex Number Theory Feather Command n The feather command draws complex numbers as arrows in the xy plane » » » » » z 1=1+2 j; z 2=3+3 j; z 3=3+j; feather(z 1, 'r'); hold on feather(z 2, 'b'); feather(z 3, 'g'); feather(z 3, 'k'); ylabel('Imaginary'); xlabel('Real'); 9

Complex Numbers: Complex Number Theory Exponential Representation n Sometimes an exponential representation of a complex number is easier to manipulate than the rectangular sum of the real and imaginary part The Complex Exponential Function ez will be used to represent a complex number whose Taylor Series Expansion is: We can assume that ez will be valid for all z 10

Complex Numbers: Complex Number Theory Exponential Series n n If z = iq, purely imaginary, where q is real, the complex exponential function can be written using a Taylor Series Expansion: Which can be separated into real and imaginary components since i raised to even powers of n will be -1 11

Complex Numbers: Complex Number Theory Derivation of Euler’s Equation n n Knowing that the Taylor Series Expansions for sine and cosine functions are: Through substitution, Euler’s Equation is derived: 12

Complex Numbers: Complex Number Theory Exponential Polar Form n n n Through Euler’s Equation we see that: This representation of a complex number is referred to as the Exponential Polar Form: Sometimes Polar Form is written using the shortened notation: 13

Complex Numbers: Complex Number Theory Plotting Polar Form n n n Graphically depicting Euler’s Equation in the First Quadrant of an Argand Diagram we see: r refers to the radius from z to the origin, commonly called the Magnitude of z q is the Angle of z with respect to the Real Axis measured in degrees or radians 14

Complex Numbers: Complex Number Theory Magnitude n n n Through use of the Pythagorean theorem, the Magnitude (radius) of a complex number always has the relationship: This relationship always holds true regardless of which quadrant of the Argand diagram that the number lies in The Magnitude of a complex number z=x+iy is denoted using Absolute Value notation 15

Complex Numbers: Complex Number Theory Angle n n n The angle, q, of a complex number z denoted by: Determining the angle of a complex number depends on the quadrant of the Argand diagram Measuring the angle counter-clockwise from the x-axis gives a positive q Measuring the angle clockwise from the x-axis gives a negative q Example: The angle of z=0+j can be represented in multiple ways 16

Complex Numbers: Complex Number Theory Angle of Quadrants I and IV Quadrant IV 17

Complex Numbers: Complex Number Theory Angle of Quadrants II and III Quadrant III 18

Complex Numbers: Complex Number Theory Purely Real or Imaginary Numbers Rectangular Polar Short Long Degrees 1 -1 j -j = = 1 + i 0 -1 +i 0 0 + i 1 0 - i 1 = = 1Ð 0° = 1Ð 180° = 1Ð 90° = 1Ð-90° = Polar Radians 1Ð 0 1Ðp/2 1Ð-p/2 19

Complex Numbers: Complex Number Theory Abs and Angle Commands n n n The abs command in Matlab returns the magnitude of a complex number The angle command returns the angle of a complex number in radians Remember that the conversion between radians and degrees is: 20

Complex Numbers: Complex Number Theory Polar Example n Use Matlab to find the magnitude and angle of z=1+i » z=1+i; » r=abs(z) r = 1. 4142 » theta_rads=angle(z) theta_rads = 0. 7854 » theta_degs=theta_rads*180/pi theta_degs = 45 21

Complex Numbers: Complex Number Theory Entering Polar Form n n Complex numbers can be directly entered into Matlab using the exponential polar form Example: Create a complex number z with a magnitude of 2 and an angle of p/2 radians » z=2*exp(i*pi/2) z = 0. 0000 + 2. 0000 i 22

Complex Numbers: Complex Number Theory Polar Plotting n n Matlab’s compass(z) or compass(x, y) command can be used to draw complex numbers on a polar plot Note that z is a complex number in rectangular form » » n z 1=3+3 i; compass(z 1) hold on compass(4, -3) Angles are displayed in degrees 23

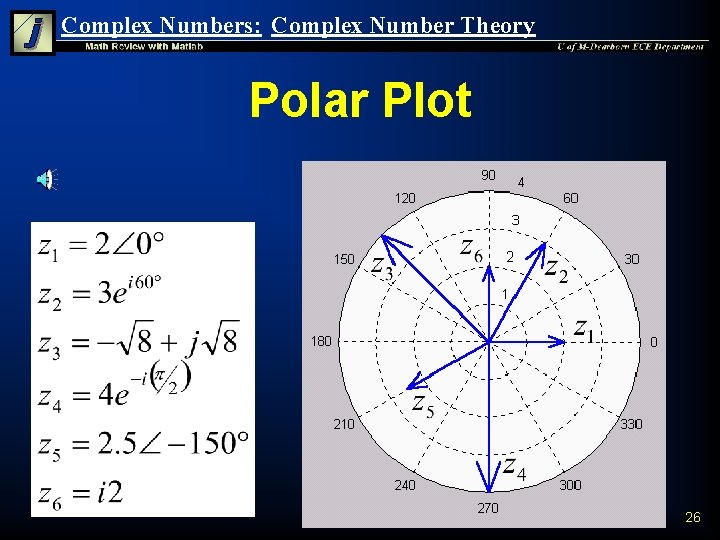
Complex Numbers: Complex Number Theory Plotting Example n Example: Plot the following complex numbers by hand. Use Matlab’s compass function to verify your results. 24

Complex Numbers: Complex Number Theory Matlab Verification z(1) = 2; z(2) = 3*exp(i*60*(pi/180)); z(3) = -(8^0. 5) + j*(8^0. 5); z(4) = 4*exp(-i*pi/2); z(5) = 2. 5*exp(-i*150*(pi/180)); z(6) = 2 i; compass(z) 25

Complex Numbers: Complex Number Theory Polar Plot 26

Complex Numbers: Complex Number Theory Summary n n Representing complex numbers in rectangular, exponential, and polar forms Using Euler’s Equation to represent real and imaginary parts of complex numbers Determining magnitude and angles of complex numbers Graphing complex numbers using Argand Diagrams 27