The Real Number System Objectives Standard 8 2

The Real Number System

Objectives Standard 8. 2 The student will describe orally and in writing the relationships between the subsets of the real number system.

Real Numbers – a combination of all the number systems. • A real number is EITHER rational, or irrational. It cannot be both. • Real numbers include natural numbers, whole numbers, integers, rational numbers, and irrational numbers. ALL NUMBERS ARE REAL NUMBERS.
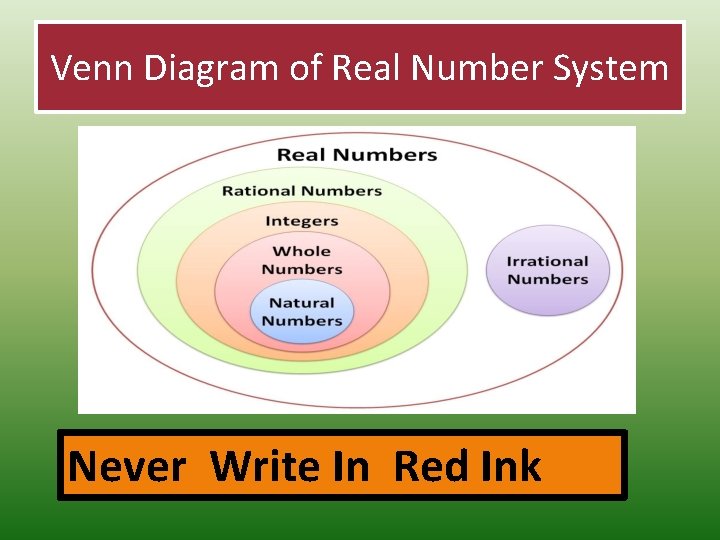
Venn Diagram of Real Number System Never Write In Red Ink

Natural Numbers Natural numbers – the numbers used for counting how many items you have. • Zero is NOT included in the set of natural numbers. • Decimals and Negative numbers are NOT included in the set of natural numbers. Example of Natural Numbers: {1, 2, 3, 4, 5, 6, …. . }

Are these natural numbers? 162 Yes 0. 35 No, it’s a decimal -3 No, it’s a negative number. No, it’s a fraction, that simplifies to. 571429 Yes. Although it’s a fraction, it simplifies to 4.

Which of the following is the set of natural numbers? A. B. C. D. … -3, -2, -1, 0, 1, 2, 3, … 1, 2, 3, 4, …. Any number that can be written in the form of a/b.

Whole Numbers Whole numbers – include natural numbers and zero. Decimals and Negative numbers are NOT included in the set of whole numbers. Example of Whole Numbers: {0, 1, 2, 3, 4, 5, 6, …}

Are these whole numbers? 0 Yes 0. 45 No, it’s a decimal -3 No, it’s a negative number. No, it’s a fraction, that simplifies to. 5 Yes. Although it’s a fraction, it simplifies to 9.

Which of the following is the set of whole numbers? A. B. C. D. … -3, -2, -1, 0, 1, 2, 3, … 1, 2, 3, 4, …. Any number that can be written in the form of a/b.

Integers – include natural numbers, the opposite of the natural numbers (negative numbers), and zero. • All whole numbers are integers. • All natural numbers are integers. • Decimals are NOT included in the set of integers. Example of Integers: {…, -2, -1, 0, 1, 2, …. }

Are these integers? -11. 46 No, it’s a decimal. -4 Yes 0 Yes No, it’s a fraction, that simplifies to. 50 2, 356 Yes.

Which statement is true? A. B. C. D. All integers are natural numbers. All integers are whole numbers. All whole numbers are natural numbers. All whole numbers are integers. Explain why the other answer choices are not true?

Which of the following numbers is a natural number, a whole number, and an integer? A. B. C. D. 3 0 0. 3 -8

Rational Numbers – a number that can be expressed as the ratio of two integers. This ratio is sometimes called a fraction. • The set of rational numbers includes integers, whole numbers and natural numbers. • Decimals are rational numbers if the decimal repeats such as with 0. 1212… or if the decimal stops/terminates such as with 432. 8. • Square roots are rational numbers if they are perfect squares.

Are these rational numbers? 0. 27 Yes, it’s a repeating decimal. 3 0. 010110111… No it does not repeat. Yes, it’s a whole number and can be written as 3/1. Yes, it’s a perfect square and simplifies to 11. Yes, it simplifies to -0. 25 which is a terminating decimal. No, the decimal form of pi is 3. 1415926…. No, the decimal form is 1. 7320508…Also it’s not a perfect square.

Which of the following numbers is NOT a rational number? A. B. C. D. 0. 2 4 5. 7 3. 121221222…

Irrational Numbers – a number that cannot be expressed as the ratio of two integers. “opposite of rational” • Decimals that are irrational never repeat and never end or terminate. • The square root of any number that is not a perfect square is irrational.

Are these irrational numbers? 0. 13 No, it repeats. 5 No 0. 010110111… Yes, it does not repeat and does not end. No, it’s a perfect square. No Yes, pi is always irrational. Yes, the decimal form is 2. 449484…Also it’s not a perfect square.

Which of the following numbers is an irrational number? A. 0. 81 B. 9. 02 C. 5 D.

Which statement is true? A. All integers are rational numbers. B. A number can be both rational and irrational. C. Every integer is a whole number. D. All natural numbers are irrational.

What is the lowest subset to which - 2 belongs? (Look at the Venn Diagram for the subsets of real numbers) A. B. C. D. Irrational Number Rational Number Whole Number Integer Although -2 is a rational number and an integer. It is an integer first which makes it the lowest subset.

Which statement is true? A. B. C. D. All real numbers are rational. All irrational numbers are real. All integers are whole numbers. All rational numbers are irrational.

Other Types of Numbers Prime Numbers – numbers that are only divisible by 1 and itself. Ex: {2, 3, 5, 7, 11, 13, 17, 19, …} Composite Numbers – numbers that are not prime numbers. {Ex: 4, 6, 8, 9, 10, 12, 14, 15, …} Even Numbers – numbers that can be divided evenly by 2. { Ex: 2, 4, 6, 8, 10, 12, 14, 16…} Odd Numbers – numbers that cannot be divided evenly by 2. { Ex: 1, 3, 5, 7, 9, 11, 13, 15, 17…}

Prime Numbers

Prime vs. Composite Numbers
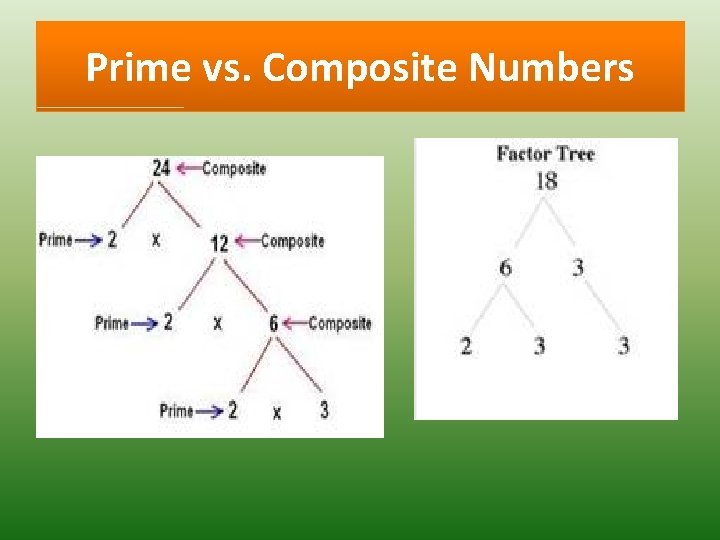
Prime vs. Composite Numbers

A = {2, 3, 5, 7, 11, 19, 23, 29} Which statement is true? A. B. C. D. All numbers in A are odd. All numbers in A are prime. All numbers in A are even. All numbers in A are composites.

Which number is composite and odd? A. B. C. D. 15 19 17 8
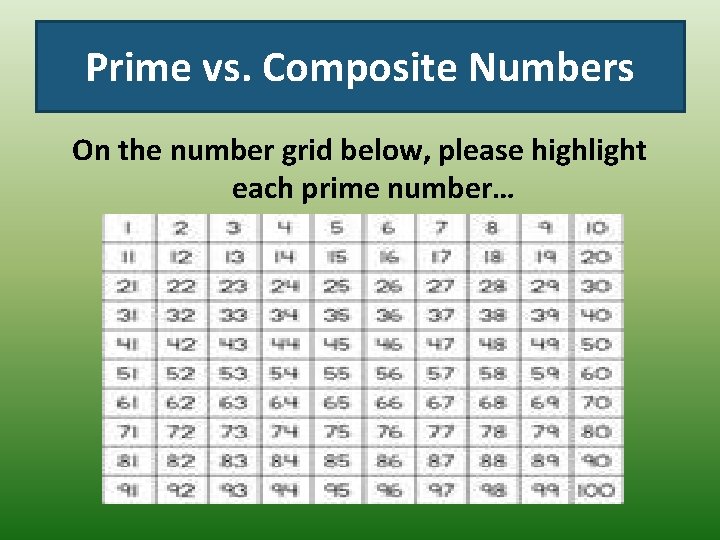
Prime vs. Composite Numbers On the number grid below, please highlight each prime number…

Prime Numbers Highlighted…
- Slides: 31