REAL NUMBERS as opposed to fake numbers Why

REAL NUMBERS (as opposed to fake numbers? )

Why do we have to review numbers Miss Price? Be a beast in Math when you know the basics!

Objective SWBAT… • Identify and classify the parts of the Real Number System By… • Visualizing the number line

Key Concepts • • • Real Number Rational Number Integer Whole Number Natural Number Irrational Number

Key Concept Real Numbers • Real Numbers are every number. • Therefore, any number that you can find on the number line.

What does it Mean? • The number line goes on forever. • Every point on the line is a REAL number. • There are no gaps on the number line. • Between the whole numbers and the fractions there are numbers that are decimals but they don’t terminate and are not recurring decimals. They go on forever.

Real Numbers REAL NUMBERS 154, 769, 852, 354 1. 333 -5, 632. 1010101256849765… -8 π 549. 23789 61 49%

Two Kinds of Real Numbers • Rational Numbers • Irrational Numbers

Key Concept Rational Numbers • A rational number is a real number that can be written as a fraction. • A rational number written in decimal form is terminating or repeating.

Examples of Rational Numbers • 16 • 1/2 • 3. 56 • -8 • 1. 3333… • - 3/4

Integers One of the subsets of rational numbers

Key Concept What are integers? • Integers are the whole numbers and their opposites. • Examples of integers are 6 -12 0 186 -934

How can you write an integer as a rational number by definition? • Integers are rational numbers because they can be written as fraction with 1 as the denominator.

Key Concept Types of Integers • Natural Numbers(N): Natural Numbers are counting numbers from 1, 2, 3, 4, 5, . . . . N = {1, 2, 3, 4, 5, . . . . } • Whole Numbers (W): Whole numbers are natural numbers including zero. They are 0, 1, 2, 3, 4, 5, . . . . W = {0, 1, 2, 3, 4, 5, . . . } W = 0 + N

Key Concept Irrational Numbers • An irrational number is a number that cannot be written as a fraction of two integers. • Irrational numbers written as decimals are non-terminating and non-repeating.

Irrational numbers : If a whole number is not a perfect square, then its square root is an irrational number. Caution! A repeating decimal may not appear to repeat on a calculator, because calculators show a finite number of digits.

Examples of Irrational Numbers • • Pi

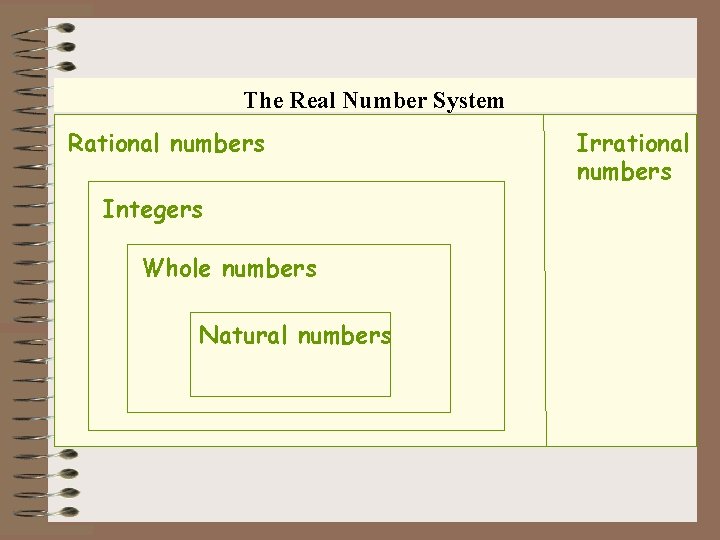
The Real Number System Rational numbers Integers Whole numbers Natural numbers Irrational numbers

The Real Number System Irrational Rational numbers • Can be represented as a fraction of 2 integers numbers Integers. … -3, -2, -1, 0, 1, 2, 3, …. Whole numbers 0, 1, 2, 3, …. Natural numbers 1, 2, 3, …. • Cannot be represented as a fraction of 2 integers

The Human Number Line Determine all of the classifications that fit for the number…

A fraction with a denominator of 0 is undefined because you cannot divide by zero. So it is not a number at all.

Determining the Classification of All Numbers State if each number is rational, irrational, or not a real number. A. 21 irrational B. 0 3 0 =0 3 rational

Determining the Classification of All Numbers State if each number is rational, irrational, or not a real number. C. 4 0 not a real number

Objective SWBAT… • compare rational and irrational numbers By… • Ordering numbers on a number line

Comparing Rational and Irrational Numbers • When comparing different forms of rational and irrational numbers, convert the numbers to the same form. Compare -3 (convert -3 3 7 and -3. 571 to -3. 428571… > -3. 571

Practice •

Ordering Rational and Irrational Numbers • To order rational and irrational numbers, convert all of the numbers to the same form. • You can also find the approximate locations of rational and irrational numbers on a number line.

Example Order these numbers from least to greatest. ¹/₄, 75%, . 04, 10%, ⁹/₇ ¹/₄ becomes 0. 25 75% becomes 0. 75 0. 04 stays 0. 04 10% becomes 0. 10 ⁹/₇ becomes 1. 2857142… Answer: 0. 04, 10%, ¹/₄, 75%, ⁹/₇

Practice Order these from least to greatest:

Objectives SWBAT… • compute with integers By… • Using the basic operation rules for integers

Examples: Use the number line if necessary. 1) (-4) + 8 = 4 2) (-1) + (-3) = -4 3) 5 + (-7) = -2

Addition Rule 1) When the signs are the same, ADD and keep the sign. (-2) + (-4) = -6 2) When the signs are different, SUBTRACT and use the sign of the larger number. (-2) + 4 = 2 2 + (-4) = -2

-1 + 3 = ? 1. 2. 3. 4. -4 -2 2 4 Answer Now

-6 + (-3) = ? 1. 2. 3. 4. -9 -3 3 9 Answer Now

The additive inverses (or opposites) of two numbers add to equal zero. Example: The additive inverse of 3 is -3 Proof: 3 + (-3) = 0 We will use the additive inverses for subtraction problems.

What’s the difference between 7 - 3 and 7 + (-3) ? 7 - 3 = 4 and 7 + (-3) = 4 The only difference is that 7 - 3 is a subtraction problem and 7 + (-3) is an addition problem. “SUBTRACTING IS THE SAME AS ADDING THE OPPOSITE. ” (Keep-change)

When subtracting, change the subtraction to adding the opposite (keep-change) and then follow your addition rule. Example #1: - 4 - (-7) - 4 + (+7) Diff. Signs --> Subtract and use larger sign. 3 Example #2: -3 -7 - 3 + (-7) Same Signs --> Add and keep the sign. -10

Which is equivalent to -12 – (-3)? 1. 2. 3. 4. Answer Now 12 + 3 -12 - 3

7 – (-2) = ? 1. 2. 3. 4. Answer Now -9 -5 5 9

Review 1) If the problem is addition, follow your addition rule. 2) If the problem is subtraction, change subtraction to adding the opposite (keep-change) and then follow the addition rule.

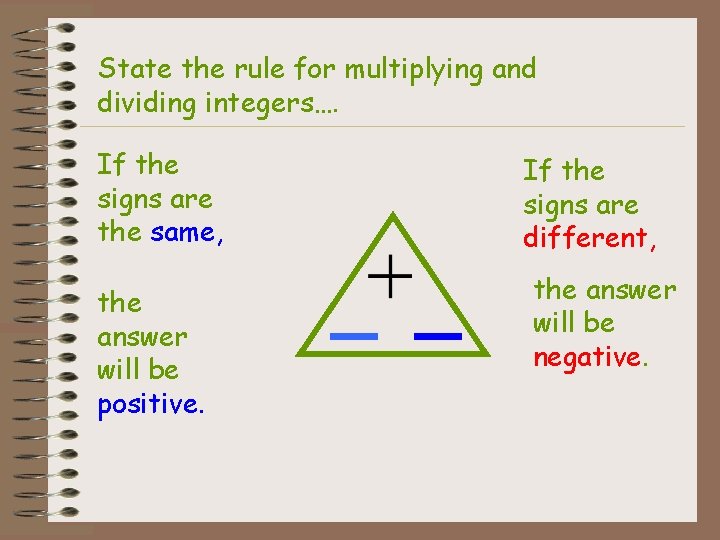
State the rule for multiplying and dividing integers…. If the signs are the same, the answer will be positive. If the signs are different, the answer will be negative.

Independent Practice Copy down the problems in your notes. The problems you don’t finish will be homework. We will review a proper homework assignment format tomorrow. 1. -8 - -7 = 2. (-3)(-4) = 3. (2)(-2) + 1 = 4. (28 – 8) ÷ (-9 - -5) = 5. If x = -10, then -2 – x = 6. Compare: ⅗ and ⅝ 7. Identify on a number line: ½, ⅜, √ 12, -0. 8 8. Prove 0. 6666666…. . is a rational number.