M OMENTUM Momentum Impulse Conservation of Momentum in

M OMENTUM! Momentum Impulse Conservation of Momentum in 1 Dimension Conservation of Momentum in 2 Dimensions Angular Momentum Torque Moment of Inertia

Momentum Defined p = mv p = momentum vector m = mass v = velocity vector

Momentum Facts • p = mv • Momentum is a vector quantity! • Velocity and momentum vectors point in the same direction. • SI unit for momentum: kg · m /s (no special name). • Momentum is a conserved quantity (this will be proven later). • A net force is required to change a body’s momentum. • Momentum is directly proportional to both mass and speed. • Something big and slow could have the same momentum as something small and fast.

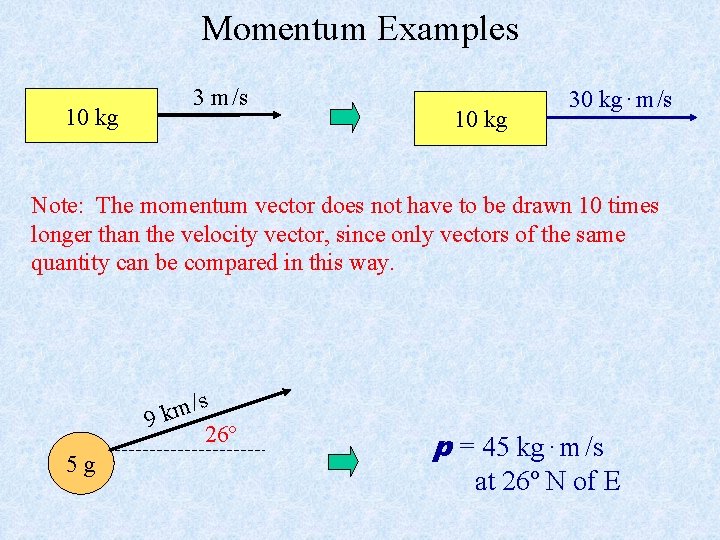
Momentum Examples 10 kg 3 m /s 10 kg 30 kg · m /s Note: The momentum vector does not have to be drawn 10 times longer than the velocity vector, since only vectors of the same quantity can be compared in this way. /s m k 9 26º 5 g p = 45 kg · m /s at 26º N of E

Equivalent Momenta Car: m = 1800 kg; v = 80 m /s p = 1. 44 · 105 kg · m /s Bus: m = 9000 kg; v = 16 m /s p = 1. 44 · 105 kg · m /s Train: m = 3. 6 · 104 kg; v = 4 m /s p = 1. 44 · 105 kg · m /s continued on next slide

Equivalent Momenta (cont. ) The train, bus, and car all have different masses and speeds, but their momenta are the same in magnitude. The massive train has a slow speed; the low-mass car has a great speed; and the bus has moderate mass and speed. Note: We can only say that the magnitudes of their momenta are equal since they’re aren’t moving in the same direction. The difficulty in bringing each vehicle to rest--in terms of a combination of the force and time required--would be the same, since they each have the same momentum.

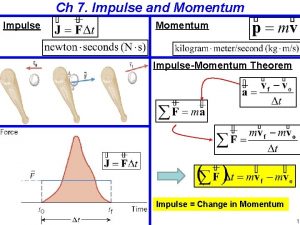
Impulse Defined Impulse is defined as the product force acting on an object and the time during which the force acts. The symbol for impulse is J. So, by definition: J=Ft Example: A 50 N force is applied to a 100 kg boulder for 3 s. The impulse of this force is J = (50 N) (3 s) = 150 N · s. Note that we didn’t need to know the mass of the object in the above example.

Impulse Units J = F t shows why the SI unit for impulse is the Newton · second. There is no special name for this unit, but it is equivalent to a kg · m /s. { proof: 1 N · s = 1 (kg · m /s 2) (s) = 1 kg · m /s Fnet = m a shows this is equivalent to a newton. Therefore, impulse and momentum have the same units, which leads to a useful theorem.

Impulse - Momentum Theorem The impulse due to all forces acting on an object (the net force) is equal to the change in momentum of the object: Fnet t = p We know the units on both sides of the equation are the same (last slide), but let’s prove theorem formally: Fnet t = m a t = m ( v / t) t = m v = p

Stopping Time Ft = Ft Imagine a car hitting a wall and coming to rest. The force on the car due to the wall is large (big F ), but that force only acts for a small amount of time (little t ). Now imagine the same car moving at the same speed but this time hitting a giant haystack and coming to rest. The force on the car is much smaller now (little F ), but it acts for a much longer time (big t ). In each case the impulse involved is the same since the change in momentum of the car is the same. Any net force, no matter how small, can bring an object to rest if it has enough time. A pole vaulter can fall from a great height without getting hurt because the mat applies a smaller force over a longer period of time than the ground alone would.

Impulse - Momentum Example A 1. 3 kg ball is coming straight at a 75 kg soccer player at 13 m/s who kicks it in the exact opposite direction at 22 m/s with an average force of 1200 N. How long are his foot and the ball in contact? answer: We’ll use Fnet t = p. Since the ball changes direction, p = m v = m (vf - v 0) = 1. 3 [22 - (-13)] = (1. 3 kg) (35 m/s) = 45. 5 kg · m /s. Thus, t = 45. 5 / 1200 = 0. 0379 s, which is just under 40 ms. During this contact time the ball compresses substantially and then decompresses. This happens too quickly for us to see, though. This compression occurs in many cases, such as hitting a baseball or golf ball.

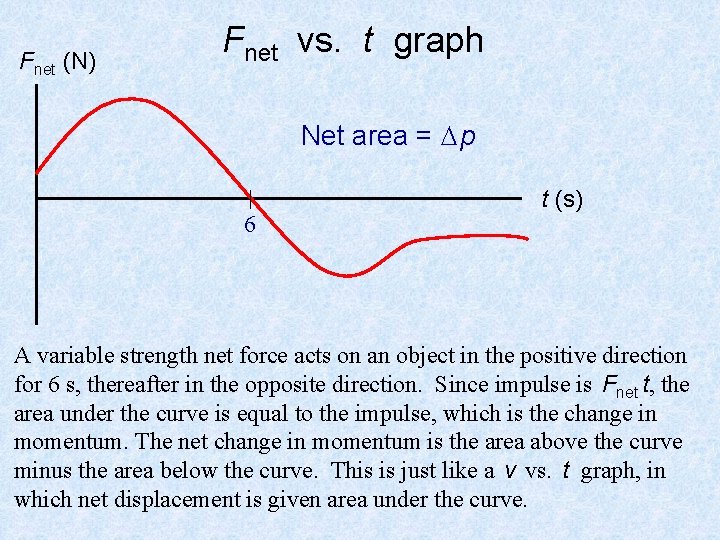
Fnet (N) Fnet vs. t graph Net area = p 6 t (s) A variable strength net force acts on an object in the positive direction for 6 s, thereafter in the opposite direction. Since impulse is Fnet t, the area under the curve is equal to the impulse, which is the change in momentum. The net change in momentum is the area above the curve minus the area below the curve. This is just like a v vs. t graph, in which net displacement is given area under the curve.

Conservation of Momentum in 1 -D Whenever two objects collide (or when they exert forces on each other without colliding, such as gravity) momentum of the system (both objects together) is conserved. This mean the total momentum of the objects is the same before and after the collision. before: p = m 1 v 1 - m 2 v 2 direction, m 2 has - momentum. ) v 2 v 1 m 1 (Choosing right as the + m 2 m 1 v 1 - m 2 v 2 = - m 1 va + m 2 vb after: p = - m 1 va + m 2 vb va m 1 m 2 vb

Directions after a collision On the last slide the boxes were drawn going in the opposite direction after colliding. This isn’t always the case. For example, when a bat hits a ball, the ball changes direction, but the bat doesn’t. It doesn’t really matter, though, which way we draw the velocity vectors in “after” picture. If we solved the conservation of momentum equation (red box) for vb and got a negative answer, it would mean that m 2 was still moving to the left after the collision. As long as we interpret our answers correctly, it matters not how the velocity vectors are drawn. v 2 v 1 m 2 m 1 v 1 - m 2 v 2 = - m 1 va + m 2 vb va m 1 m 2 vb

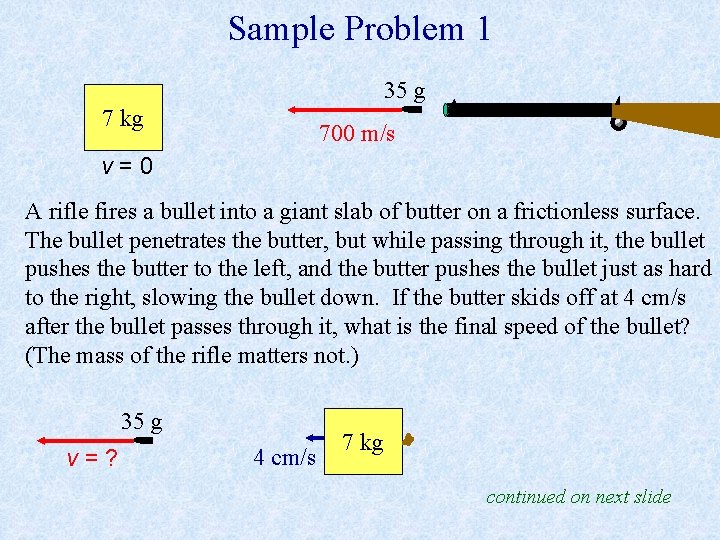
Sample Problem 1 35 g 7 kg 700 m/s v=0 A rifle fires a bullet into a giant slab of butter on a frictionless surface. The bullet penetrates the butter, but while passing through it, the bullet pushes the butter to the left, and the butter pushes the bullet just as hard to the right, slowing the bullet down. If the butter skids off at 4 cm/s after the bullet passes through it, what is the final speed of the bullet? (The mass of the rifle matters not. ) 35 g v=? 4 cm/s 7 kg continued on next slide

Sample Problem 1 (cont. ) Let’s choose left to be the + direction & use conservation of momentum, converting all units to meters and kilograms. 35 g p before = 7 (0) + (0. 035) (700) 7 kg = 24. 5 kg · m /s v=0 35 g 4 cm/s v=? p before = p after 7 kg 700 m/s p after = 7 (0. 04) + 0. 035 v = 0. 28 + 0. 035 v 24. 5 = 0. 28 + 0. 035 v v = 692 m/s v came out positive. This means we chose the correct direction of the bullet in the “after” picture.

Sample Problem 2 35 g 7 kg 700 m/s v=0 Same as the last problem except this time it’s a block of wood rather than butter, and the bullet does not pass all the way through it. How fast do they move together after impact? v 7. 035 kg (0. 035) (700) = 7. 035 v v = 3. 48 m/s Note: Once again we’re assuming a frictionless surface, otherwise there would be a frictional force on the wood in addition to that of the bullet, and the “system” would have to include the table as well.

Proof of Conservation of Momentum The proof is based on Newton’s 3 rd Law. Whenever two objects collide (or exert forces on each other from a distance), the forces involved are an action-reaction pair, equal in strength, opposite in direction. This means the net force on the system (the two objects together) is zero, since these forces cancel out. F F M m force on M due to m force on m due to M For each object, F = (mass) (a) = (mass) ( v / t ) = (mass v) / t = p / t. Since the force applied and the contact time is the same for each mass, they each undergo the same change in momentum, but in opposite directions. The result is that even though the momenta of the individual objects changes, p for the system is zero. The momentum that one mass gains, the other loses. Hence, the momentum of the system before equals the momentum of the system after.

Conservation of Momentum applies only in the absence of external forces! In the first two sample problems, we dealt with a frictionless surface. We couldn’t simply conserve momentum if friction had been present because, as the proof on the last slide shows, there would be another force (friction) in addition to the contact forces. Friction wouldn’t cancel out, and it would be a net force on the system. The only way to conserve momentum with an external force like friction is to make it internal by including the tabletop, floor, or the entire Earth as part of the system. For example, if a rubber ball hits a brick wall, p for the ball is not conserved, neither is p for the ballwall system, since the wall is connected to the ground and subject to force by it. However, p for the ball-Earth system is conserved!

Sample Problem 3 An apple is originally at rest and then dropped. After falling a short time, it’s moving pretty fast, say at a speed V. Obviously, momentum is not conserved for the apple, since it didn’t have any at first. How can this be? answer: Gravity is an external force on the apple V m F v Earth M F apple, so momentum for it alone is not conserved. To make gravity “internal, ” we must define a system that includes the other object responsible for the gravitational force--Earth. The net force on the apple-Earth system is zero, and momentum is conserved for it. During the fall the Earth attains a very small speed v. So, by conservation of momentum: m. V = M v

Sample Problem 4 A crate of raspberry donut filling collides with a tub of lime Kool Aid on a frictionless surface. Which way on how fast does the Kool Aid rebound? answer: Let’s draw v to the right in the after picture. 3 (10) - 6 (15) = -3 (4. 5) + 15 v v = -3. 1 m/s Since v came out negative, we guessed wrong in drawing v to the right, but that’s OK as long as we interpret our answer correctly. After the collision the lime Kool Aid is moving 3. 1 m/s to the left. before 3 kg after 10 m/s 4. 5 m/s 3 kg 6 m/s 15 kg v

Conservation of Momentum in 2 -D To handle a collision in 2 -D, we conserve momentum in each dimension separately. Choosing down & right as positive: m 1 v 1 m 2 2 v 2 1 a m 1 va m 2 vb b before: px = m 1 v 1 cos 1 - m 2 v 2 cos 2 py = m 1 v 1 sin 1 + m 2 v 2 sin 2 after: px = -m 1 va cos a + m 2 vb cos b py = m 1 va sin a + m 2 vb sin b Conservation of momentum equations: m 1 v 1 cos 1 - m 2 v 2 cos 2 = -m 1 va cos a + m 2 vb cos b m 1 v 1 sin 1 + m 2 v 2 sin 2 = m 1 va sin a + m 2 vb sin b

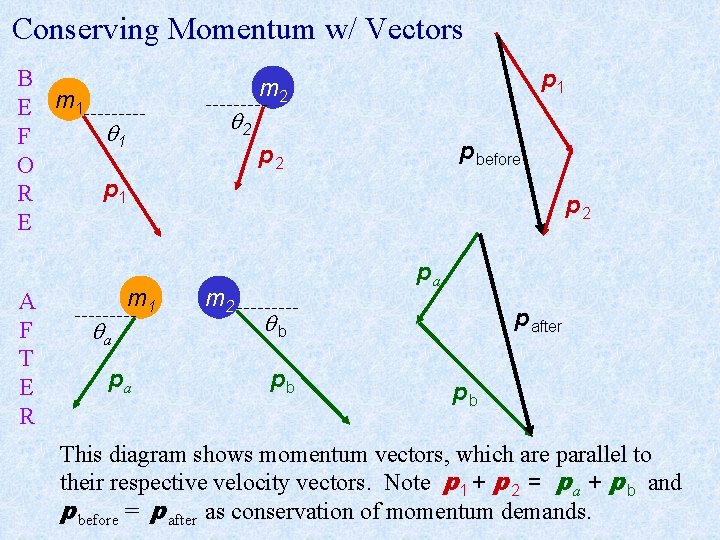
Conserving Momentum w/ Vectors B E m 1 1 F O p 1 R E A F T E R a m 1 pa 2 p 1 m 2 p before p 2 m 2 pa p after b pb pb This diagram shows momentum vectors, which are parallel to their respective velocity vectors. Note p 1 + p 2 = p a + p b and p before = p after as conservation of momentum demands.

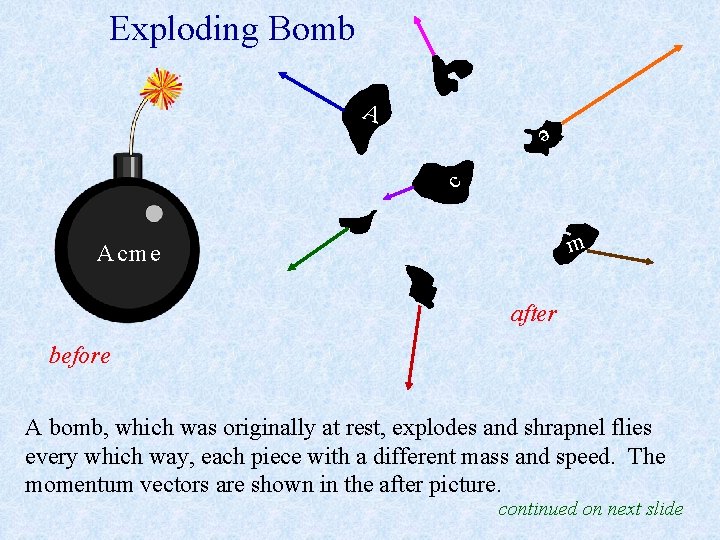
Exploding Bomb A e c m Acme after before A bomb, which was originally at rest, explodes and shrapnel flies every which way, each piece with a different mass and speed. The momentum vectors are shown in the after picture. continued on next slide

Exploding Bomb (cont. ) Since the momentum of the bomb was zero before the explosion, it must be zero after it as well. Each piece does have momentum, but the total momentum of the exploded bomb must be zero afterwards. This means that it must be possible to place the momentum vectors tip to tail and form a closed polygon, which means the vector sum is zero. If the original momentum of the bomb were not zero, these vectors would add up to the original momentum vector.

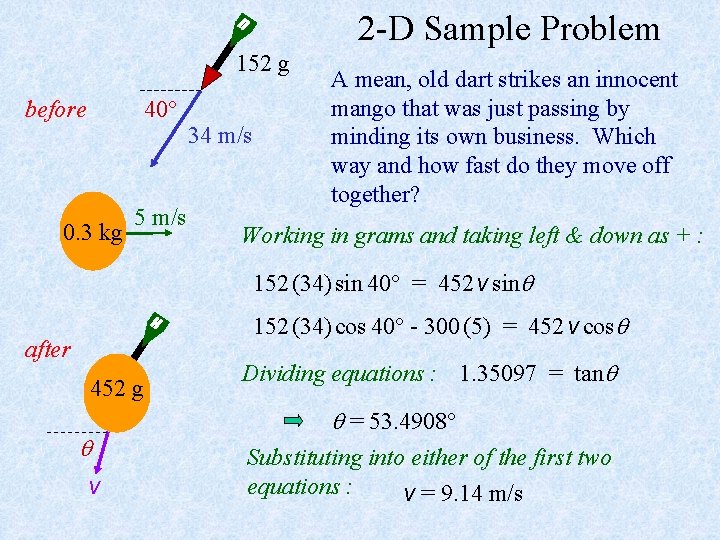
2 -D Sample Problem 152 g before 40 0. 3 kg 5 m/s 34 m/s A mean, old dart strikes an innocent mango that was just passing by minding its own business. Which way and how fast do they move off together? Working in grams and taking left & down as + : 152 (34) sin 40 = 452 v sin 152 (34) cos 40 - 300 (5) = 452 v cos after 452 g v Dividing equations : 1. 35097 = tan = 53. 4908 Substituting into either of the first two equations : v = 9. 14 m/s

Alternate Solution 40 5168 Shown are momentum vectors (in g m/s). The black vector is the total momentum before the collision. Because of conservation of momentum, it is also the total momentum after the collisions. We can use trig to find its magnitude and direction. p 40 1500 Law of Cosines : p 2 = 5168 2 + 1500 2 - 2 5168 1500 cos 40 p = 4132. 9736 g m/s Dividing by total mass : v = (4132. 9736 g m/s) / (452 g) = 9. 14 m/s Law of Sines : sin 1500 sin 40 = 4132. 9736 = 13. 4908 Angle w/ resp. to horiz. = 40 + 13. 4908 53. 49

Comments on Alternate Method • Note that the alternate method gave us the exact same solution. • This method can only be used when two objects collide and stick, or when one object breaks into two. Otherwise, we’d be dealing with a polygon with more sides than a triangle. • In using the Law of Sines (last step), the angle involved (ß) is the angle inside the triangle. A little geometry gives us the angle with respect to the horizontal.

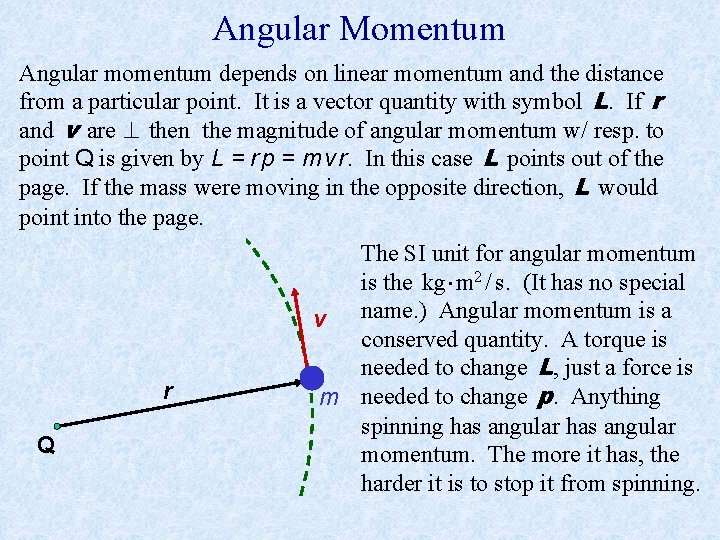
Angular Momentum Angular momentum depends on linear momentum and the distance from a particular point. It is a vector quantity with symbol L. If r and v are then the magnitude of angular momentum w/ resp. to point Q is given by L = r p = m v r. In this case L points out of the page. If the mass were moving in the opposite direction, L would point into the page. The SI unit for angular momentum is the kg m 2 / s. (It has no special v name. ) Angular momentum is a conserved quantity. A torque is needed to change L, just a force is r m needed to change p. Anything spinning has angular Q momentum. The more it has, the harder it is to stop it from spinning.

Angular Momentum: General Definition If r and v are not then the angle between these two vectors must be taken into account. The general definition of angular momentum is given by a vector cross product: L = r p This formula works regardless of the angle. As you know from our study of cross products, the magnitude of the angular momentum of m relative to point Q is: L = r p sin = m v r. In this case, by the right-hand rule, L points out of the page. If the mass were moving in the opposite direction, L would point into the page. v r Q m

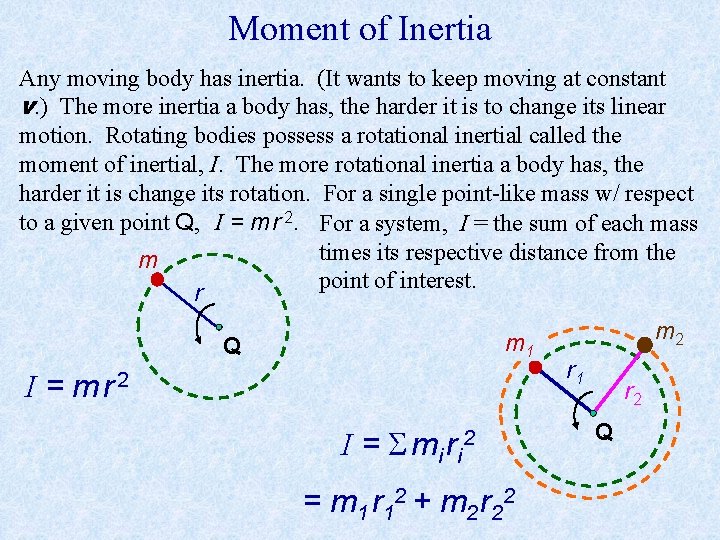
Moment of Inertia Any moving body has inertia. (It wants to keep moving at constant v. ) The more inertia a body has, the harder it is to change its linear motion. Rotating bodies possess a rotational inertial called the moment of inertial, I. The more rotational inertia a body has, the harder it is change its rotation. For a single point-like mass w/ respect to a given point Q, I = m r 2. For a system, I = the sum of each mass times its respective distance from the m point of interest. r m 1 Q I= mr 2 I= mi ri 2 = m 1 r 1 2 + m 2 r 2 2 m 2 r 1 r 2 Q

Moment of Inertia Example Two merry-go-rounds have the same mass and are spinning with the same angular velocity. One is solid wood (a disc), and the other is a metal ring. Which has a bigger moment of inertia relative to its center of mass? r r m m answer: I is independent of the angular speed. Since their masses and radii are the same, the ring has a greater moment of inertia. This is because more of its mass is farther from the axis of rotation. Since I is bigger for the ring, it would more difficult to increase or decrease its angular speed.

Angular Acceleration As you know, acceleration is when an object speeds up, slows down, or changes directions. Angular acceleration occurs when a spinning object spins faster or slower. Its symbol is , and it’s defined as: = / t Note how this is very similar to a = v / t for linear acceleration. Ex: If a wind turbine spinning at 21 rpm speeds up to 30 rpm over 10 s due to a gust of wind, its average angular acceleration is 9 rpm / 10 s. This means every second it’s spinning 9 revolutions per minute faster than the second before. Let’s convert the units: 9 rpm 9 rev / min 9 (2 rad) 2 = = = 0. 094 rad / s = 10 s min 10 s (60 s) 10 s Since a radian is really dimensionless (a length divided by a length), the SI unit for angular acceleration is the “per second squared” (s-2).

Torque & Angular Acceleration Newton’s 2 nd Law, as you know, is Fnet = m a The 2 nd Law has a rotational analog: net = I A force is required for a body to undergo acceleration. A “turning force” (a torque) is required for a body to undergo angular acceleration. The bigger a body’s mass, the more force is required to accelerate it. Similarly, the bigger a body’s rotational inertia, the more torque is required to accelerate it angularly. Both m and I are measures of a body’s inertia (resistance to change in motion).

Linear Momentum & Angular Momentum If a net force acts on an object, it must accelerate, which means its momentum must change. Similarly, if a net torque acts on a body, it undergoes angular acceleration, which means its angular momentum changes. Recall, angular momentum’s magnitude is given by L = mvr r v m (if v and r are perpendicular) So, if a net torque is applied, angular velocity must change, which changes angular momentum. proof: net = r Fnet = r m a = r m v / t = L / t So net torque is the rate of change of angular momentum, just as net force is the rate of change of linear momentum. continued on next slide

Linear & Angular Momentum (cont. ) Here is yet another pair of similar equations, one linear, one rotational. From the formula v = r , we get L = m v r = m r (r ) = m r 2 = I This is very much like p = m v, and this is one reason I is defined the way it is. In terms of magnitudes, linear momentum is inertia times speed, and angular momentum is rotational inertia times angular speed. L = I p = mv

Spinning Ice Skater Why does a spinning ice skater speed up when she pulls her arms in? Suppose Mr. Stickman is sitting on a stool that swivels holding a pair of dumbbells. His axis of rotation is vertical. With the weights far from that axis, his moment of inertia is large. When he pulls his arms in as he’s spinning, the weights are closer to the axis, so his moment of inertia gets much smaller. Since L = I and L is conserved, the product of I and is a constant. So, when he pulls his arms in, I goes down, goes up, and he starts spinning much faster. I = L = I

Comparison: Linear & Angular Momentum Linear Momentum, p Angular Momentum, L • Tendency for a mass to continue moving in a straight line. rotating. • Parallel to v. • Perpendicular to both v and r. • A conserved, vector quantity. • Magnitude is inertia (mass) times speed. • Magnitude is rotational inertia times angular speed. • Net force required to change it. • Net torque required to change it. • The greater the mass, the greater • The greater the moment of the force needed to change inertia, the greater the torque momentum. needed to change angular momentum.