LP SOCP and optimizationfree approaches to sum of

![Application II: Machine learning and statistics Example: Shape-constrained regression [Ahmadi, Curmei, H. ] 5 Application II: Machine learning and statistics Example: Shape-constrained regression [Ahmadi, Curmei, H. ] 5](https://slidetodoc.com/presentation_image/f91208f2a4f4b24fe9880ba42e7354bd/image-5.jpg)

















- Slides: 32

LP, SOCP, and optimization-free approaches to sum of squares optimization Georgina Hall Princeton, ORFE 1

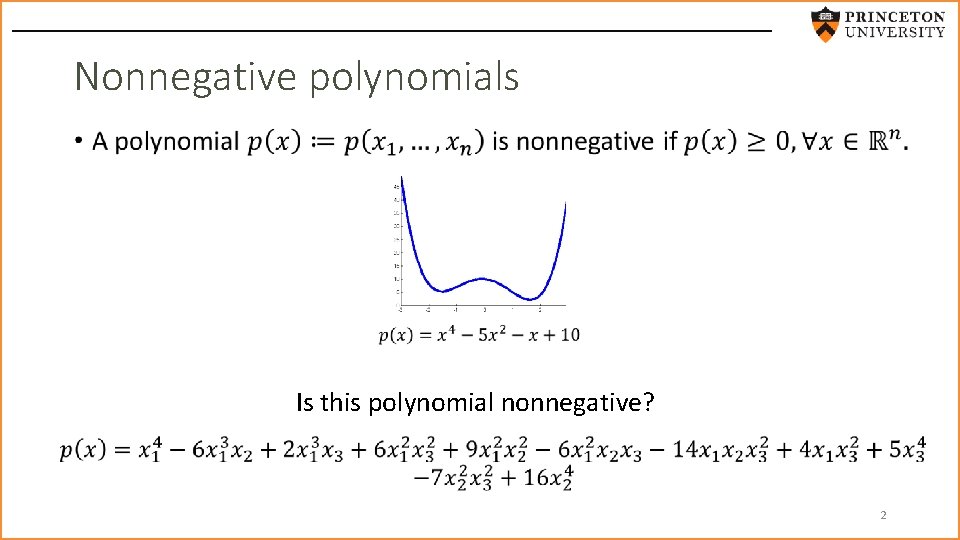
Nonnegative polynomials • Is this polynomial nonnegative? 2

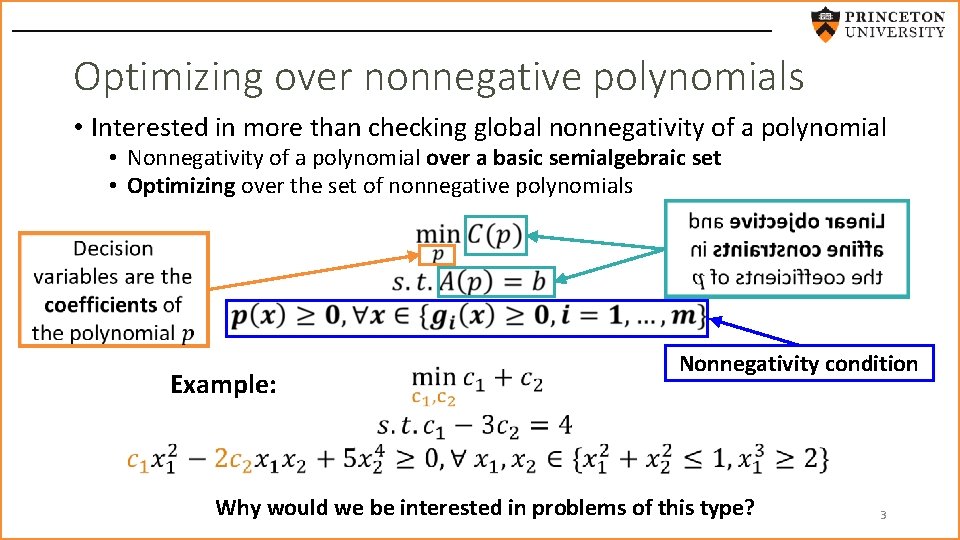
Optimizing over nonnegative polynomials • Interested in more than checking global nonnegativity of a polynomial • Nonnegativity of a polynomial over a basic semialgebraic set • Optimizing over the set of nonnegative polynomials Example: Nonnegativity condition Why would we be interested in problems of this type? 3

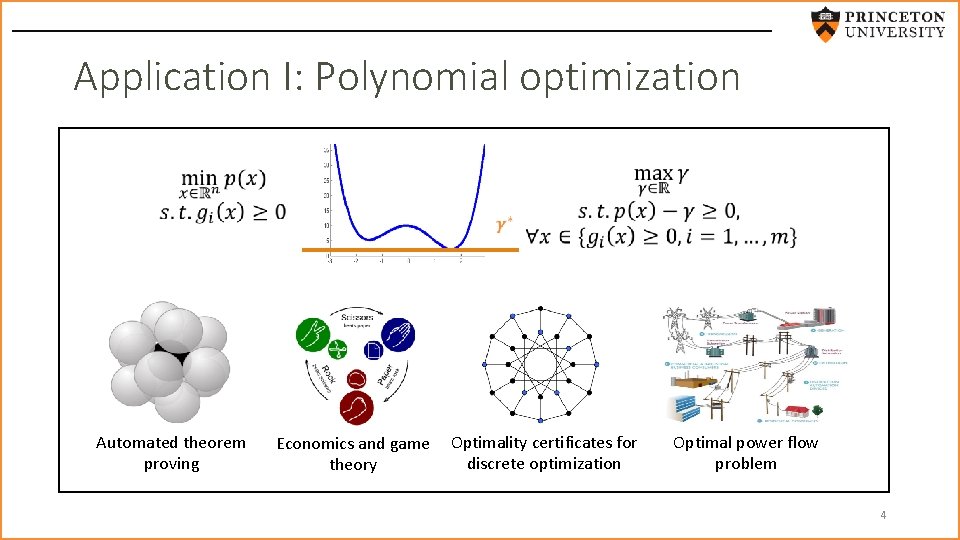
Application I: Polynomial optimization Automated theorem proving Economics and game Optimality certificates for discrete optimization theory Optimal power flow problem 4
![Application II Machine learning and statistics Example Shapeconstrained regression Ahmadi Curmei H 5 Application II: Machine learning and statistics Example: Shape-constrained regression [Ahmadi, Curmei, H. ] 5](https://slidetodoc.com/presentation_image/f91208f2a4f4b24fe9880ba42e7354bd/image-5.jpg)
Application II: Machine learning and statistics Example: Shape-constrained regression [Ahmadi, Curmei, H. ] 5

Application III: Control Automated search for Lyapunov functions for dynamical systems Dynamical system: Properties of interest: Stability of equilibrium points Collision avoidance 6

Sum of squares polynomials • Ex: 7

How to optimize over nonnegative polynomials? (1/2) Optimizing over nonnegative polynomials Sum of squares program 8

How to optimize over nonnegative polynomials? (2/2) Semidefinite program Sum of squares program Challenge: • Question: How to avoid SDP when optimizing over nonnegative polynomials? 9

This talk Linear programming (LP) and second order cone programming (SOCP) alternatives to SOS An optimization-free Positivstellensatz for polynomial optimization problems Replace sos program: dsos/sdsos polynomials + improvements Part I Overview of other work (brief) New certificate Part III 10

Part I LP and SOCP-based alternatives to SOS optimization 11

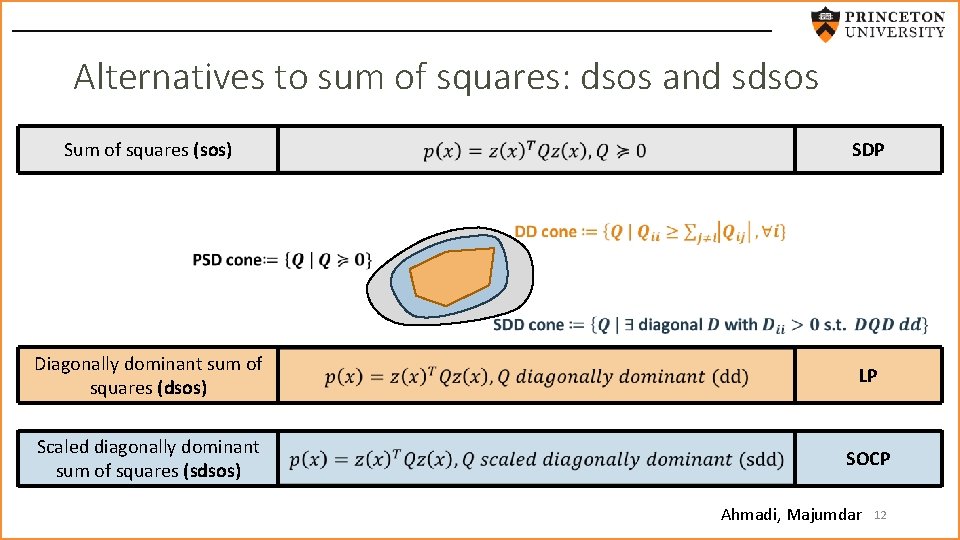
Alternatives to sum of squares: dsos and sdsos Sum of squares (sos) SDP Diagonally dominant sum of squares (dsos) LP Scaled diagonally dominant sum of squares (sdsos) SOCP Ahmadi, Majumdar 12

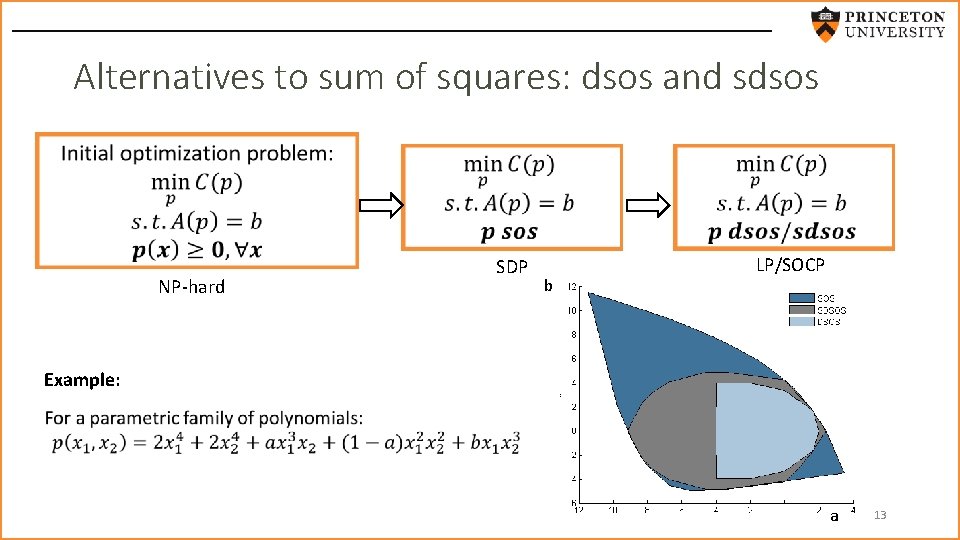
Alternatives to sum of squares: dsos and sdsos NP-hard SDP b LP/SOCP Example: a 13

Improvements on dsos and sdsos Replacing sos polynomials by dsos/sdsos polynomials: • +: fast bounds • - : not always as good quality (compared to sos) Iteratively construct a sequence of improving LP/SOCPs Initialization: Start with the dsos/sdsos polynomials Method 1: Basis Pursuit Method 2: Column Generation 14

Method 1: Basis pursuit (1/3) dd in the “right basis” psd but not dd 15

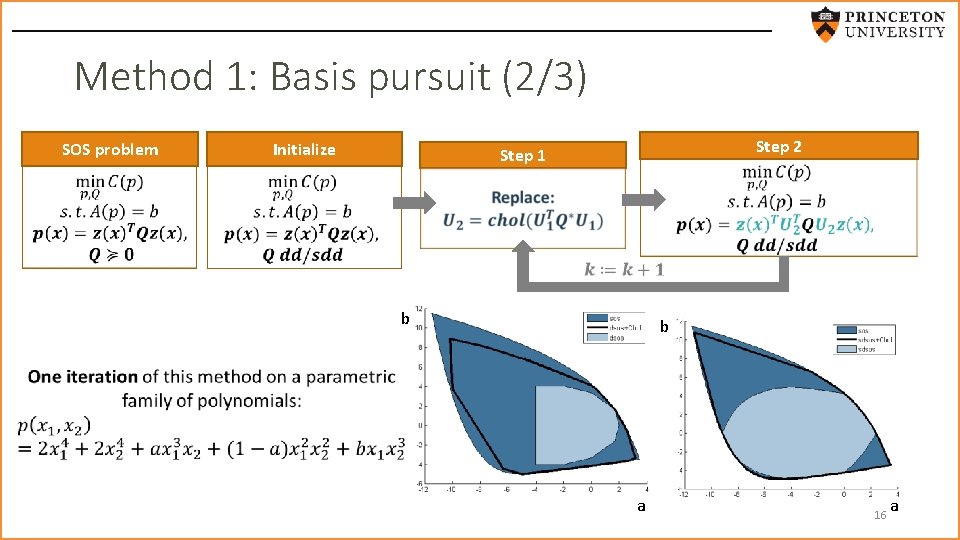
Method 1: Basis pursuit (2/3) Initialize SOS problem Step 2 Step 1 new basis b b a 16 a

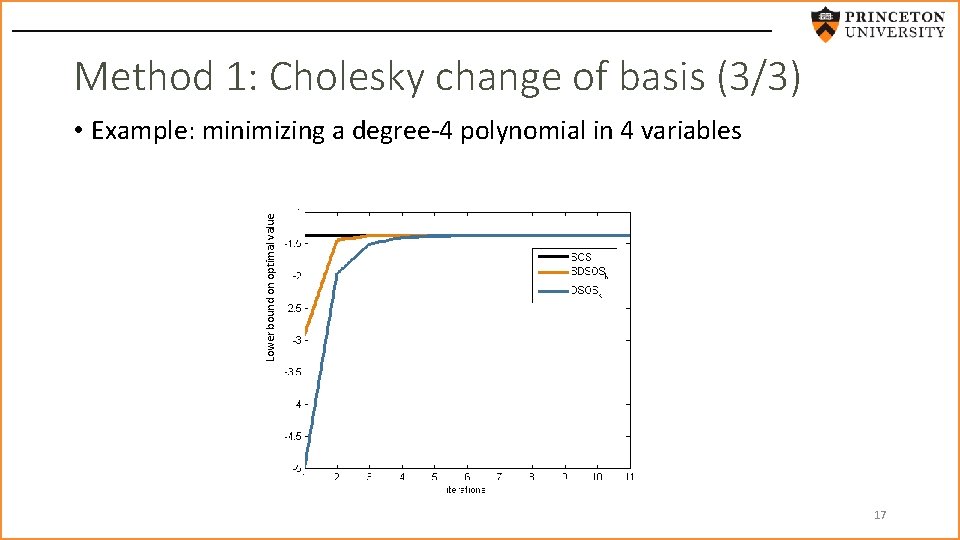
Method 1: Cholesky change of basis (3/3) Lower bound on optimal value • Example: minimizing a degree-4 polynomial in 4 variables 17

Method 2: Column generation (1/4) • Focus on LP-based version of this method (SOCP is similar). SOS problem Replace DSOS problem with DSOS problem [In collaboration with A. A. Ahmadi and S. Dash, IBM Research] 18

Method 2: Column generation (2/4) DSOS problem Using ② Idea behind the algorithm: 19

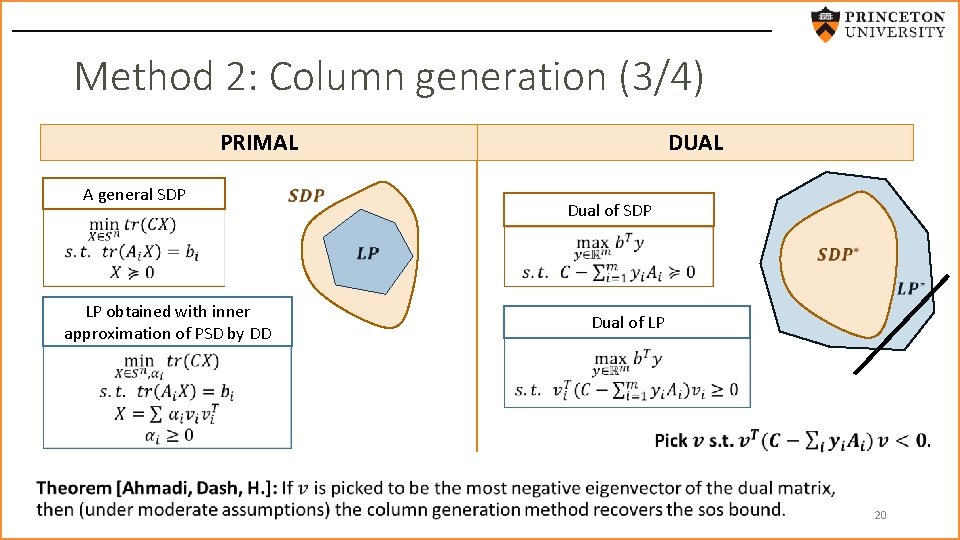
Method 2: Column generation (3/4) PRIMAL A general SDP DUAL Dual of SDP LP obtained with inner approximation of PSD by DD Dual of LP 20

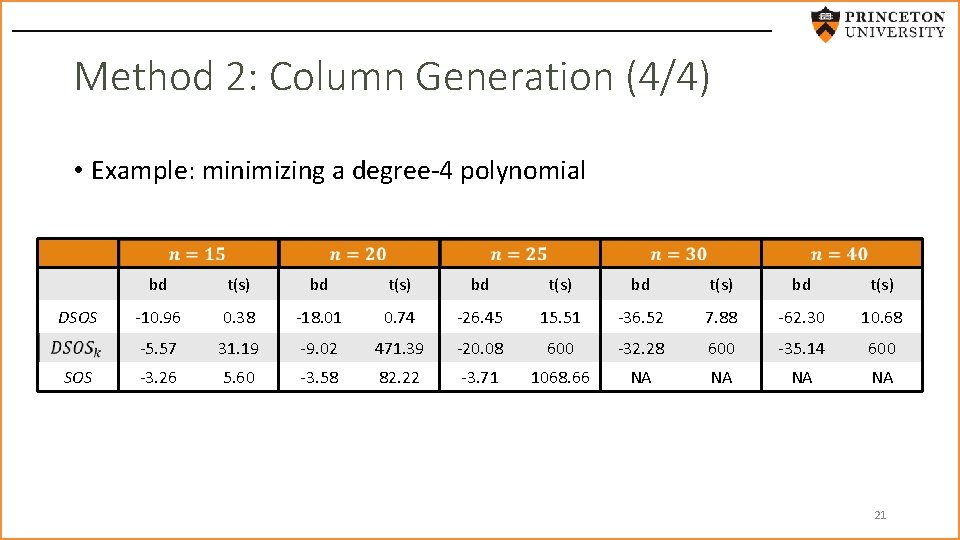
Method 2: Column Generation (4/4) • Example: minimizing a degree-4 polynomial DSOS bd t(s) bd t(s) -10. 96 0. 38 -18. 01 0. 74 -26. 45 15. 51 -36. 52 7. 88 -62. 30 10. 68 -5. 57 31. 19 -9. 02 471. 39 -20. 08 600 -32. 28 600 -35. 14 600 -3. 26 5. 60 -3. 58 82. 22 -3. 71 1068. 66 NA NA 21

Part II An optimization-free Positivstellensatz for lower bounds on polynomial optimization problems (POPs) 22

Lower bounds on POPs POP • 23

An optimization-free method for lower bounds (1/2) POP 24

An optimization-free method for lower bounds (2/2) Proof sketch of theorem: • 25

Part III Other work 26

Other work (1/2) With A. A. Ahmadi, A. Makadia (Google Brain), and V. Sindhwani (Google Brain) How to contain a cloud of points within a polynomial sublevel set of minimum volume? With A. A. Ahmadi and E. de Klerk (Tilburg University) When does a polynomial produce a norm? How can we optimize over the set of polynomial norms? 27

Other work (2/2) With E. Abbe (Princeton University) and A. Bandeira (NYU) With A. A. Ahmadi Can any polynomial be written as a difference of two convex polynomials? Can this decomposition be found efficiently? Is it unique? How does this impact the class of problems called “difference of convex programs”? [Winner of the 2016 INFORMS Computing Society Best Student Paper Award] 28

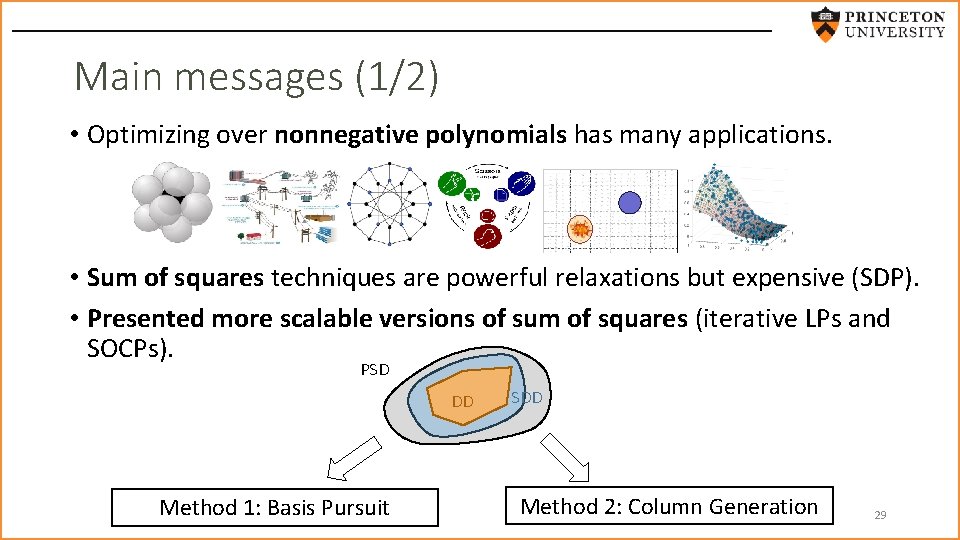
Main messages (1/2) • Optimizing over nonnegative polynomials has many applications. • Sum of squares techniques are powerful relaxations but expensive (SDP). • Presented more scalable versions of sum of squares (iterative LPs and SOCPs). PSD DD Method 1: Basis Pursuit SDD Method 2: Column Generation 29

Main messages (2/2) • Provided a hierarchy of lower bounds on polynomial optimization problems that does not require optimization. • Relies on multiplying two polynomials together and checking nonnegativity of the resulting polynomial’s coefficients. • Discussed other work. 30

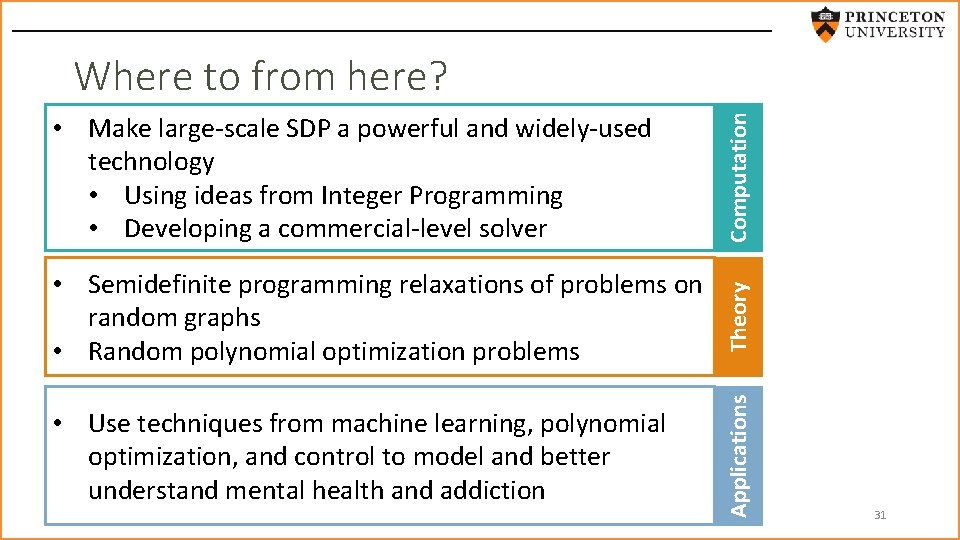
• Semidefinite programming relaxations of problems on random graphs • Random polynomial optimization problems Theory • Use techniques from machine learning, polynomial optimization, and control to model and better understand mental health and addiction Applications • Make large-scale SDP a powerful and widely-used technology • Using ideas from Integer Programming • Developing a commercial-level solver Computation Where to from here? 31

Thank you for listening Questions? Want to know more? http: //scholar. princeton. edu/ghall/ 32
 Int sum(int a int n) int sum=0 i
Int sum(int a int n) int sum=0 i Wid, wad, gad
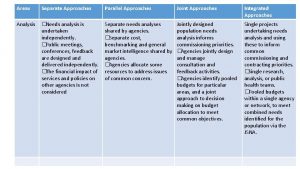
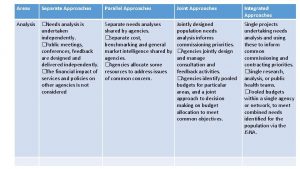
Wid, wad, gad A company's resources and capabilities represent
A company's resources and capabilities represent Semantic structure of a word
Semantic structure of a word Intrinsic and extrinsic approach to literature
Intrinsic and extrinsic approach to literature Formalist-substantivist debate
Formalist-substantivist debate Content based task based and participatory approaches
Content based task based and participatory approaches Health promotion approach
Health promotion approach Ib approaches to learning
Ib approaches to learning Essay-translation approach
Essay-translation approach Discourse and register analysis approaches
Discourse and register analysis approaches Solomon four group design
Solomon four group design Teacher dominated approach
Teacher dominated approach Historical changeability of semantic structure
Historical changeability of semantic structure Ap psychology module 2 review
Ap psychology module 2 review Develop new approaches to public governance and engagement
Develop new approaches to public governance and engagement Cost approaches and techniques in suppler assessment
Cost approaches and techniques in suppler assessment Katherine miller organizational communication
Katherine miller organizational communication Data quality and data cleaning an overview
Data quality and data cleaning an overview Data integration problems approaches and perspectives
Data integration problems approaches and perspectives Pricing considerations and approaches
Pricing considerations and approaches Learning approaches, theory, and practice
Learning approaches, theory, and practice Langue and parole
Langue and parole Linear perspective ap psychology
Linear perspective ap psychology Power bi governance services
Power bi governance services Research philosophies and approaches
Research philosophies and approaches Sum and diff identities
Sum and diff identities Sum and product softuni
Sum and product softuni 5-5 practice multiple-angle and product-to-sum identities
5-5 practice multiple-angle and product-to-sum identities Find six rational numbers between 3 and 4
Find six rational numbers between 3 and 4 Difference of two cubes formula
Difference of two cubes formula Product to sum rules
Product to sum rules Difference formula for sine
Difference formula for sine