Iterative LP and SOCP relaxations for certifying polynomial

Iterative LP and SOCP relaxations for certifying polynomial nonnegativity Georgina Hall Princeton University Joint work with: Amir Ali Ahmadi (Princeton University) Sanjeeb Dash (IBM)

BANYULS 2016 SDPs and polynomial nonnegativity (1/5) •

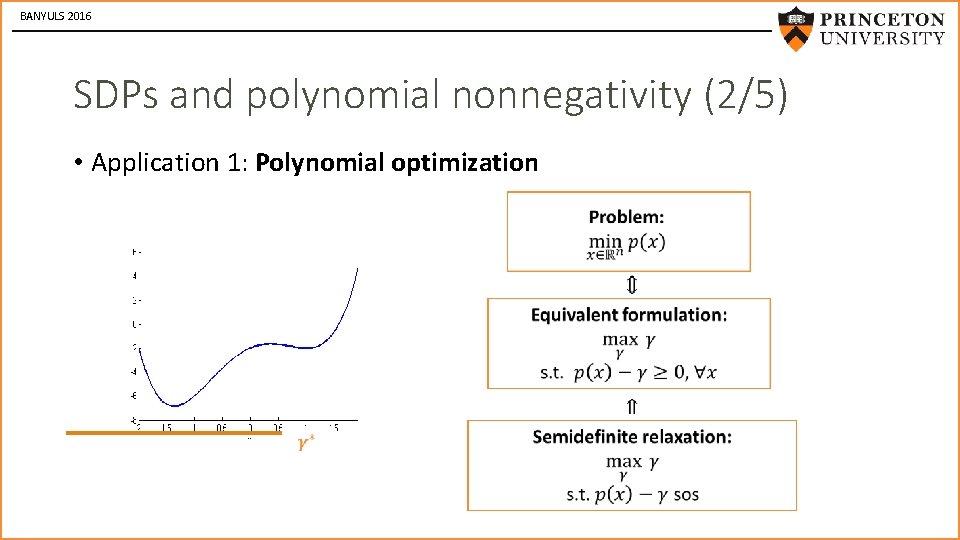
BANYULS 2016 SDPs and polynomial nonnegativity (2/5) • Application 1: Polynomial optimization

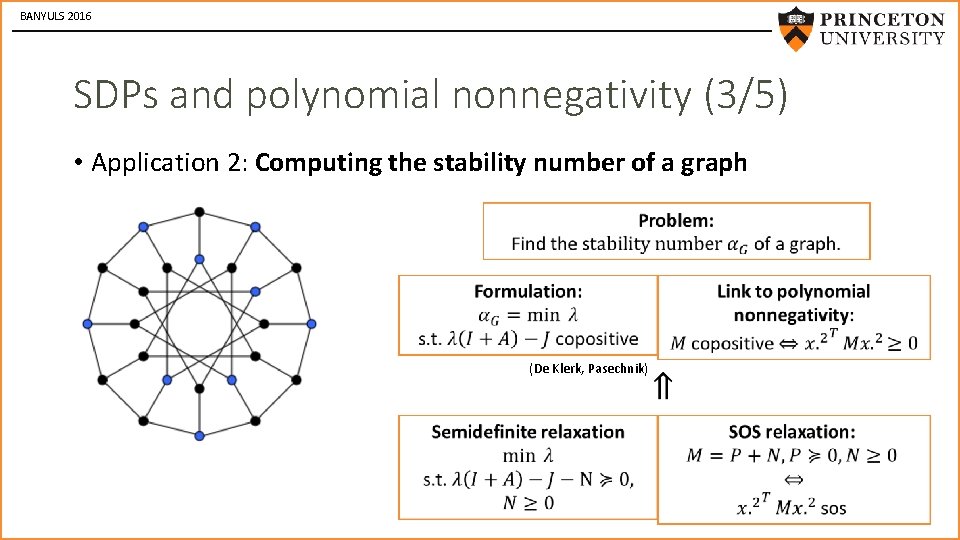
BANYULS 2016 SDPs and polynomial nonnegativity (3/5) • Application 2: Computing the stability number of a graph (De Klerk, Pasechnik)

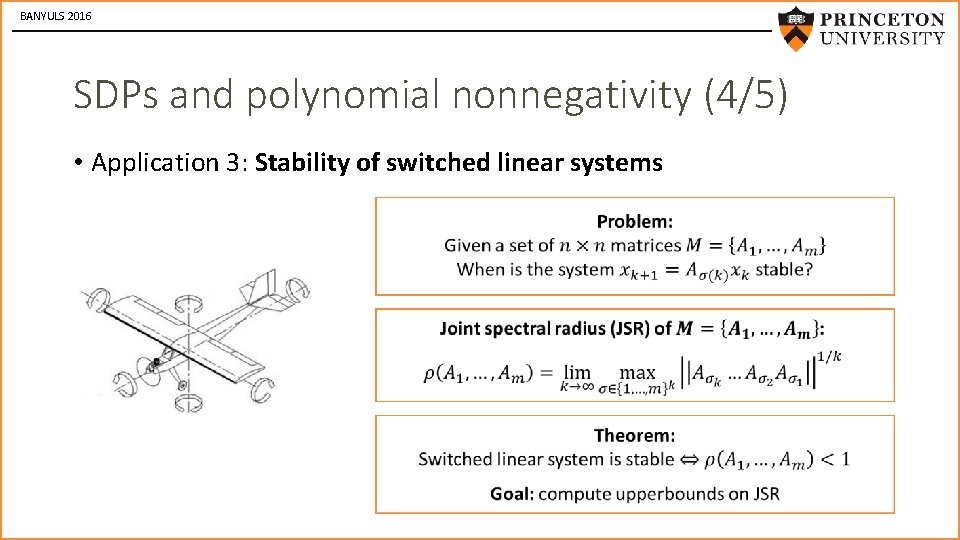
BANYULS 2016 SDPs and polynomial nonnegativity (4/5) • Application 3: Stability of switched linear systems

BANYULS 2016 SDPs and polynomial nonnegativity (5/5) • Application 3: Stability of switched linear systems (cont’d)

BANYULS 2016 Semidefinite programming: pros and cons • +: high-quality bounds for nonconvex problems. • - : can take too long to solve if psd constraint is too big. Polynomial optimization: Stability number of a graph • Typical laptop cannot minimize a degree-4 polynomial in more than a couple dozen variables. (PC: 3. 4 GHz, 16 Gb RAM)

BANYULS 2016 LP and SOCP-based inner approximations (1/2) Problem Idea SDPs do not scale well Replace psd cone by LP or SOCP representable cones • Candidate (Ahmadi, Majumdar)

BANYULS 2016 LP and SOCP-based inner approximations (2/2) Replacing psd cone by dd/sdd cones: • +: fast bounds • - : not always as good quality (compared to SDP) Iteratively construct a sequence of improving LP/SOCP-based cones Initialization: Start with the DD/SDD cone Method 1: Cholesky change of basis Method 2: Column Generation Method 3: r-s/dsos hierarchy

BANYULS 2016 Method 1: Cholesky change of basis (1/3) dd in the “right basis” psd but not dd

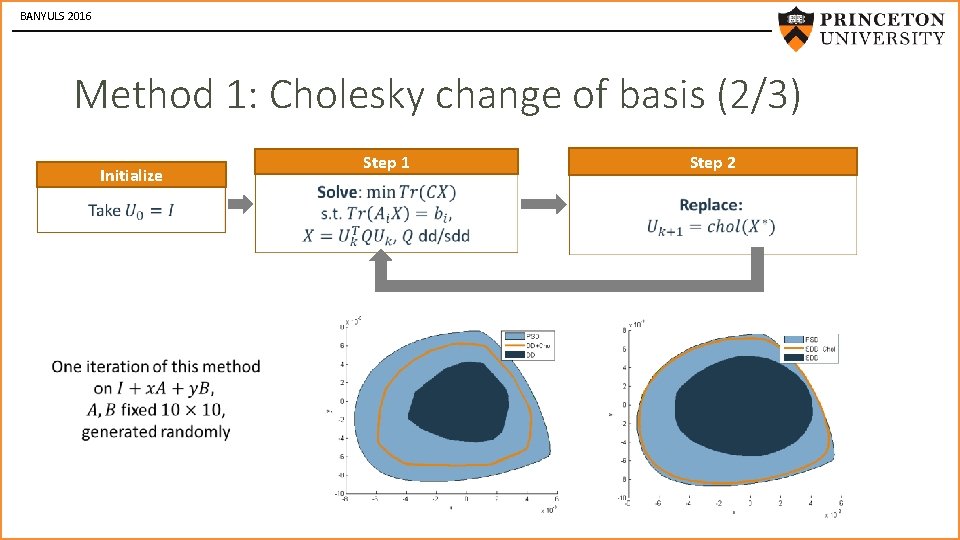
BANYULS 2016 Method 1: Cholesky change of basis (2/3) Initialize Step 1 Step 2

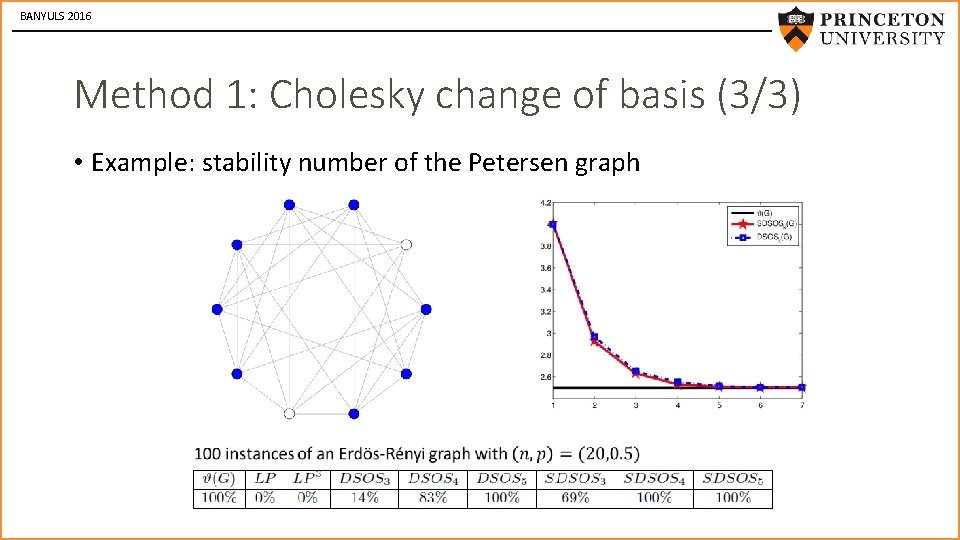
BANYULS 2016 Method 1: Cholesky change of basis (3/3) • Example: stability number of the Petersen graph

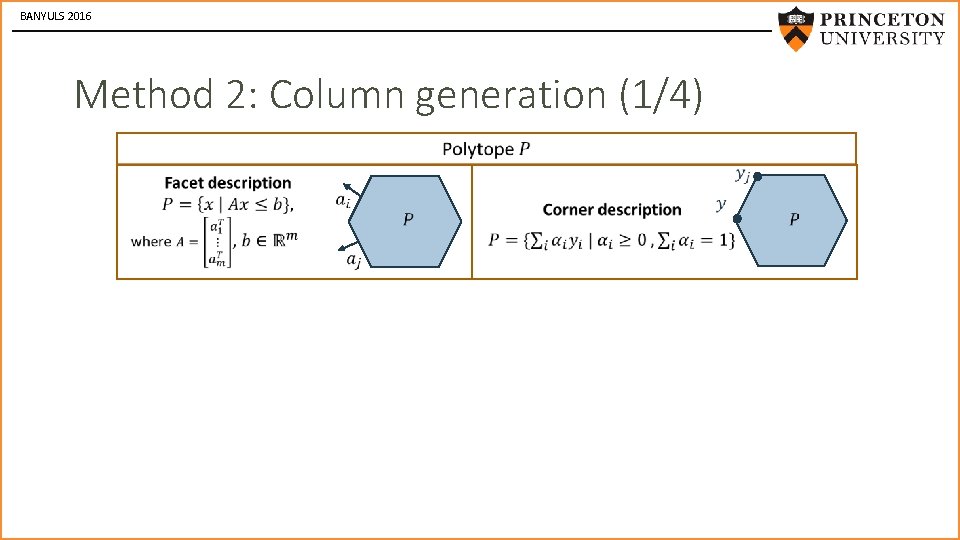
BANYULS 2016 Method 2: Column generation (1/4) DD cone SDD cone Facet description Extreme ray description + + +

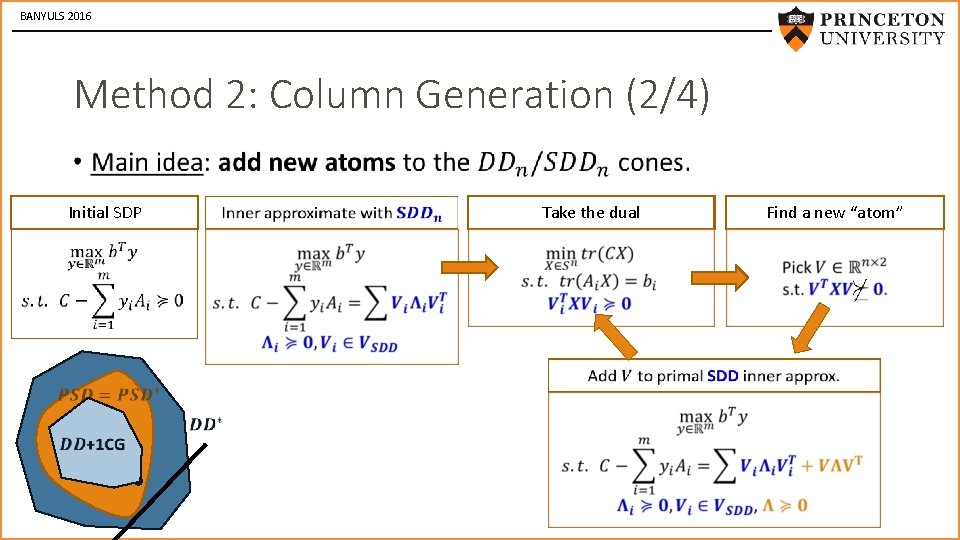
BANYULS 2016 Method 2: Column Generation (2/4) • Initial SDP Take the dual Find a new “atom”

BANYULS 2016 Method 2: Column Generation (3/4) •

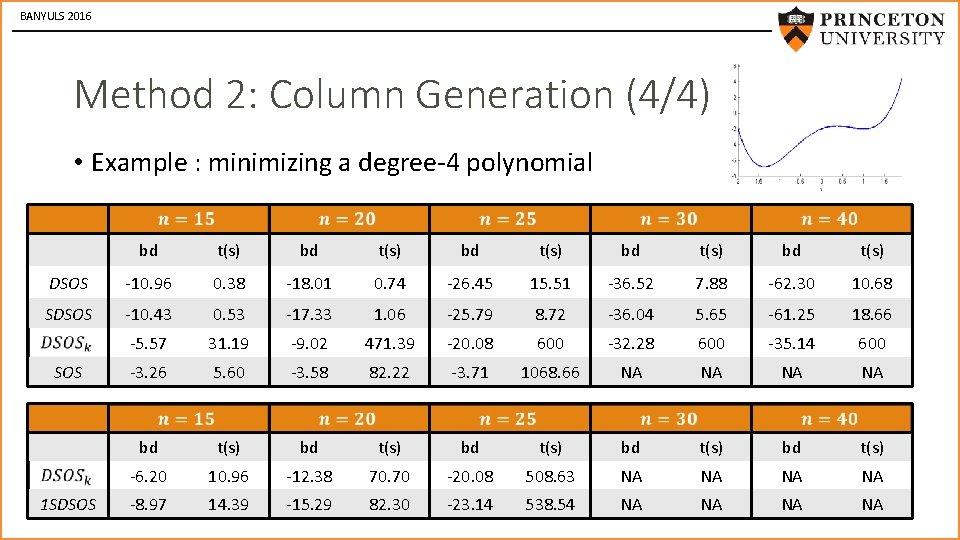
BANYULS 2016 Method 2: Column Generation (4/4) • Example : minimizing a degree-4 polynomial bd t(s) bd t(s) DSOS -10. 96 0. 38 -18. 01 0. 74 -26. 45 15. 51 -36. 52 7. 88 -62. 30 10. 68 SDSOS -10. 43 0. 53 -17. 33 1. 06 -25. 79 8. 72 -36. 04 5. 65 -61. 25 18. 66 -5. 57 31. 19 -9. 02 471. 39 -20. 08 600 -32. 28 600 -35. 14 600 -3. 26 5. 60 -3. 58 82. 22 -3. 71 1068. 66 NA NA bd t(s) bd t(s) -6. 20 10. 96 -12. 38 70. 70 -20. 08 508. 63 NA NA -8. 97 14. 39 -15. 29 82. 30 -23. 14 538. 54 NA NA SOS 1 SDSOS

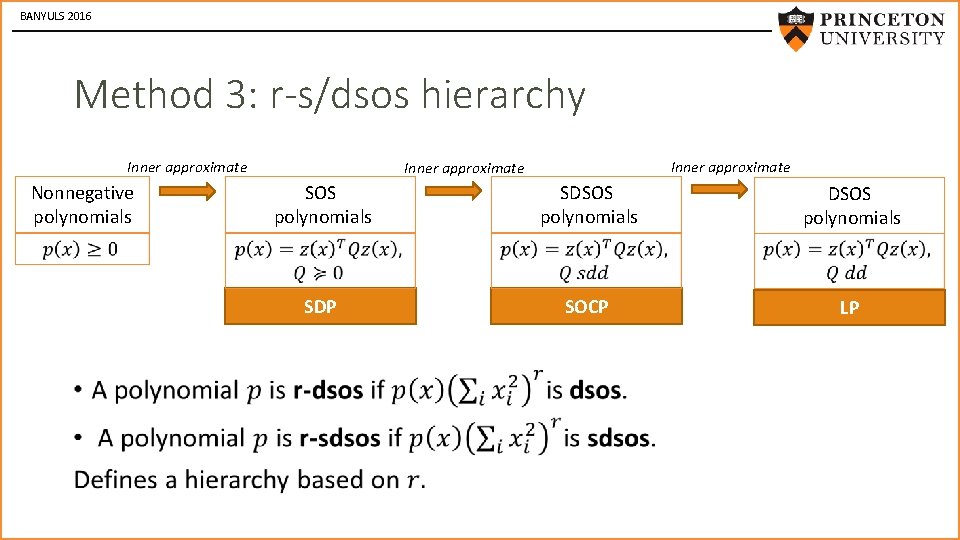
BANYULS 2016 Method 3: r-s/dsos hierarchy • Inner approximate SOS polynomials Nonnegative polynomials Inner approximate SDSOS polynomials SDP DSOS polynomials SOCP LP

BANYULS 2016 Method 3: r-s/dsos hierarchy b b a a

BANYULS 2016 Method 3: r-s/dsos hierarchy Theorem [Ahmadi, Majumdar] Any even positive definite form p is r-dsos for some r. Proof: Follows from a result by Polya. • Proof of positivity using LP. • Note that r-dsos can outperform sos, e. g. , is not sos but is 1 -dsos.

BANYULS 2016 Method 3: r-s/dsos hierarchy •

BANYULS 2016 Method 3: r-s/dsos hierarchy •

BANYULS 2016 Main messages • Can construct iterative inner approximations of the cone of nonnegative polynomials using LPs and SOCPs. • Presented three methods: Cholesky change of basis Initialization Column Generation r-s/dsos hierarchies Initialize with dsos/sdsos polynomials (or dd/sdd matrices) Method Rotate existing “atoms” of the cone of dsos/sdsos polynomials Add new atoms to the extreme rays of the cone of dsos/sdsos polynomials Use multipliers to certify nonnegativity of more polynomials. Size of the LP/SOCPs obtained Does not grow (but possibly denser) Grows slowly Grows quickly Objective taken into consideration Yes No Can beat the SOS bound No No Yes

Thank you for listening Questions? Want to learn more? http: //scholar. princeton. edu/ghall 23