lments de Calcul Tensoriel l I Les Tenseurs











- Slides: 13

Éléments de Calcul Tensoriel l. I Les Tenseurs l II Les Opérateurs Différentiels J. C. Charmet © 2002

I Les Tenseurs l I-1 l I-2 l I-3 l I-4 l I-5 Définition des Tenseurs Opérations sur les Tenseurs Symétrie et Antisymétrie Tenseurs Identité et d’Antisymétrie Produits Scalaire et Vectoriel

I-1 Définition des Tenseur : Opérateur liant dans un même repère deux grandeurs physiques en un même point d’un espace de dimension d u Ses composantes dans un repère donné M v ne dépendent que du M = u = T(M) v Le Rang d’un tenseur caractérise son nombre d’indices T(0) Tenseur de Rang 0 : Scalaire à d 0 =1 composante T(M) T(1) Tenseur de Rang 1 : Vecteur à d 1 composantes Ti(M) T(2) Tenseur de Rang 2 : Matrice à d 2 composantes Tij(M) T(n) Tenseur de Rang n : Matrice à dn composantes Tij…n(M)

I-2 Opérations sur les Tenseurs Addition tensorielle (+) : Tenseurs de même Rang C(n) = A(n) + B(n) Cij…n = Aij…n + Bij…n Produit tensoriel ( ) Cij…n…n+m = Aij…n Bij…m C(n+m) = A(n) B(m) Produit Contracté (·) sur l’indice k C(n+m-2) = A(n) · Cij…n+m-2 = B(m) d S Aij…k. . . n Bij…k…m k=1 La contraction peut s’effectuer sur plusieurs indices, chaque contraction diminuant de 2 le rang du tenseur contracté résultant Convention des indices muets Un indice de contraction, indice répété dit muet, implique la sommation sur l’ensemble des valeurs {1…d} prises par cet indice C(2) = A(2) · B(2) 3 Cij = S Aik. Bkj = Ai 1 B 1 j + Ai 2 B 2 j + Ai 2 B 3 j k=1

I-3 Symétrie et Antisymétrie Symétrie par rapport au couple d’indices l, r C(t) symétrique {l, r} C(t) antisymétrique {l, r} Cij…l…r…t = Cij…r…l. . . t Cij…l…r…t = -Cij…r…l. . . t Symétrie complète le couple d’indices a, b {1. . t} C(t) symétrie complète C(t) antisymétrique complète Cij…a…b…t = Cij…b…a. . . t Cij…a…b…t = (-1)PCij…b…a. . . t P étant la parité de la permutation {ij…a…b…t} {ij…b…a…t} Exemple : {1. 2… 4. 5. 6. 7… 9} {1. 2… 7. 5. 4. 6… 9} Paire P = 0 modulo 2 {1. 2… 4. 5. 6. 7… 9} {1. 2… 6. 7. 5. 4… 9} Impaire P = 1 modulo 2 Les propriétés de Symétrie et d’Antisymétrie sont intrinsèques Elles se conservent par changement de repère

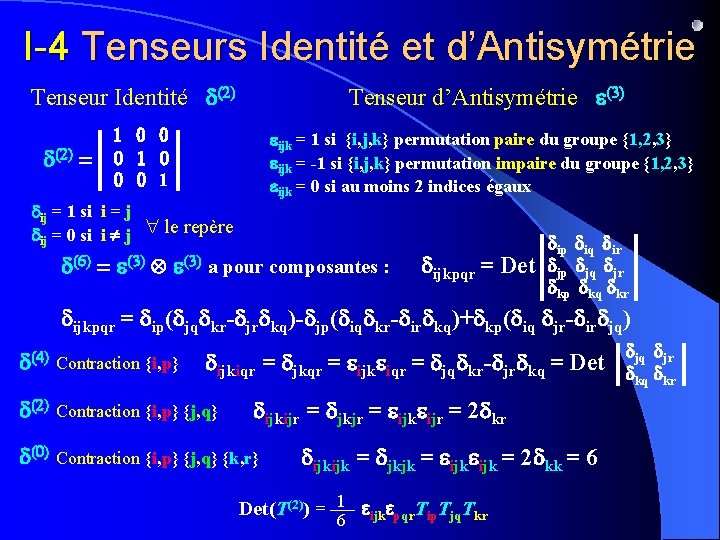
I-4 Tenseurs Identité et d’Antisymétrie Tenseur Identité d(2) = Tenseur d’Antisymétrie e(3) 1 0 0 0 1 eijk = 1 si {i, j, k} permutation paire du groupe {1, 2, 3} eijk = -1 si {i, j, k} permutation impaire du groupe {1, 2, 3} eijk = 0 si au moins 2 indices égaux dij = 1 si i = j dij = 0 si i j le repère d(6) = e(3) a pour composantes : dijkpqr = Det dip diq dir djp djq djr dkp dkq dkr dijkpqr = dip(djqdkr-djrdkq)-djp(diqdkr-dirdkq)+dkp(diq djr-dirdjq) d(4) Contraction {i, p} d d dijkiqr = djkqr = eijkeiqr = djqdkr-djrdkq = Det djq djr kq kr d(2) Contraction {i, p} {j, q} dijkijr = djkjr = eijkeijr = 2 dkr d(0) Contraction {i, p} {j, q} {k, r} dijkijk = djkjk = eijk = 2 dkk = 6 Det(T(2)) = 1 eijkepqr. Tip. Tjq. Tkr 6

I-5 Produits Scalaire et Vectoriel Produit Tensoriel de deux Vecteurs u 1 u = u 2 u 3 v 1 v = v 2 v 3 C(2) = u v = Produit Scalaire de deux Vecteurs u 1 v 1 u 1 v 2 u 1 v 3 u 2 v 1 u 2 v 2 u 2 v 3 u 3 v 1 u 3 v 2 u 3 v 3 u · v = ukvk = Ckk = Tr( u v ) Produit Extérieur de deux Vecteurs 0 u 1 v 2 -u 2 v 1 u 1 v 3 -u 3 v 1 0 u 2 v 3 -u 3 v 2 P(2) = u v - v u = u 2 v 1 -u 1 v 2 u 3 v 1 -u 1 v 3 u 3 v 2 -u 2 v 3 0 Produit Vectoriel de deux Vecteurs w=u v = u 2 v 3 – u 3 v 2 u 3 v 1 – u 1 v 3 u 2 v 1 – u 1 v 2 Cij = uivj w 1 P 23 w = w 2 = P 31 w 3 P 21 = C(2) - t. C(2) w = u v = e(3) · ·{u v } wi = eijk. Cjk

II Les Opérateurs Différentiels l l l II-1 II-2 II-3 II-4 II-5 Le Gradient La Divergence Le Rotationnel d’un Vecteur Les Rotationnels d’un Tenseur de Rang 2 Le Laplacien

II-1 Le Gradient d’un Scalaire f(x) Gradient d’un Vecteur u(x) df =Gradf·dx Gradf = du =Gradu·dx f x 1 f x 2 f x 3 u 1 x 1 u 2 Grad u = x 1 u 3 x 1 Gradient d’un Tenseur de Rang 2 T(2)(x) Gijk = Grad(3)T (2) = u 1 x 2 u 2 x 2 u 3 x 2 u 1 x 3 u 2 x 3 u 3 x 2 d. T (2) =Grad(3)T (2) ·dx Tij xk

II-2 La Divergence uk u 1 u 2 u 3 Divu = = + + xk x 1 x 2 x 3 Divergence d’un Vecteur u(x) Divergences d’un tenseur de Rang 2 T(2)(x) Divergences des Vecteurs Ligne Div. DT (2) = Tij xj = T 11 T 12 + + x 1 x 2 T 21 T 22 + + x 1 x 2 T 31 T 32 + + x 1 x 2 Div. DT(2) = Div. Gt. T(2) Div. GT(2) = Div. Dt. T(2) T 13 x 3 T 23 x 3 T 33 x 3 Divergences des Vecteurs Colonne Div. GT (2) = Tij xi = T 11 T 21 + + x 1 x 2 T 12 T 22 + + x 1 x 2 T 13 T 23 + + x 1 x 2 T 31 x 3 T 32 x 3 T 33 x 3 T(2) = t. T(2) symétrie Div. DT(2) = Div. GT(2)

II-3 Le Rotationnel d’un Vecteur x 1 = x 2 x 3 Opérateur Nabla et Gradient u 1 u = u 2 u 3 t. Grad u = Div u = ·u = Tr( u ) = Tr(Grad u ) Divergence Tenseur Rotationnel 0 Rot u = t. Grad Pseudo Vecteur Rotationnel Rot u = u u 1 x 1 u 1 x 2 u 1 x 3 = u 3 x 2 u 1 x 3 u 1 x 2 - u 2 x 3 u 3 x 1 u 2 x 1 u - Grad u = u 1 x 2 u 1 x 3 - u 2 x 1 u 3 x 1 u 2 x 1 - u 1 x 2 0 u 2 x 3 u 3 - x 2 Rot u = e(3) · ·{Gradu } [Rot u ]i = eijk uk xj u 2 x 1 u 2 x 2 u 2 x 3 u 3 x 1 u 3 x 2 u 3 x 3 u 3 x 1 u 3 x 2 u 1 x 3 u 2 x 3 0

II-4 Rotationnels d’un Tenseur Gradient d’un tenseur de Rang 2 T (2)(x) F= Grad(3)T(2) Fijk = (2) T Tij xk Pseudo Rotationnels d’un tenseur de Rang 2 T(2)(x) Rotationnels des Vecteurs Ligne == Rot. D T T 13 x 2 T 23 x 2 T 33 x 2 - T 12 x 3 T 22 x 3 T 32 x 3 [Rot. D T=]lk = ekij T 11 T 13 x 3 - x 1 T 23 x 3 - x 1 T 33 x 3 - x 1 t. Rot Tlj xi T 12 T 11 x 1 - x 2 T 21 x 1 - x 2 T 31 x 1 - x 2 T = Rot. Gt. T D t. Rot T = Rot. Dt. T G Rotationnels des Vecteurs Colonne == Rot. G T T 31 x 2 T 11 x 3 T 21 x 1 - T 21 x 3 T 31 x 1 T 11 x 2 [Rot. GT=]kl = ekij T 32 T 22 x 2 - x 3 T 12 T 32 x 3 - x 1 T 22 T 12 x 1 - x 2 Tjl xi T 33 T 23 x 2 - x 3 T 13 T 33 x 3 - x 1 T 23 T 13 x 1 - x 2 T = t. T symétrie Rot. DT = t. Rot. GT

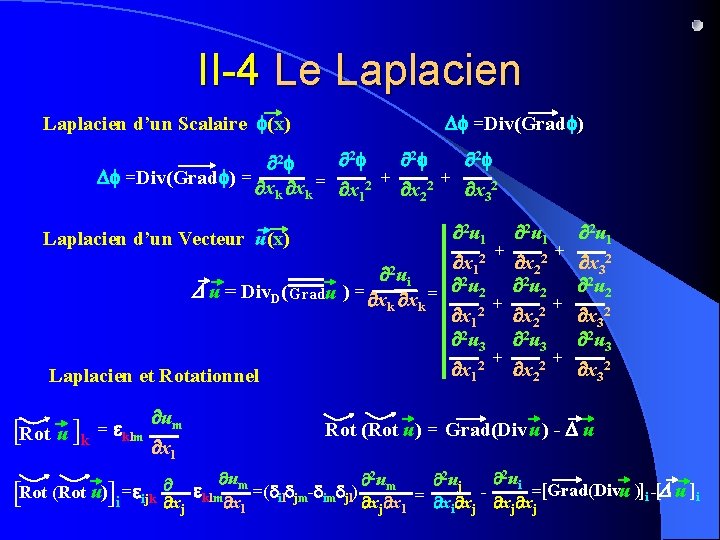
II-4 Le Laplacien d’un Scalaire f(x) Df =Div(Gradf) 2 f 2 f + + Df =Div(Gradf) = xk xk = x 12 x 22 x 32 2 u 1 + + 2 2 x x x 32 1 2 2 ui 2 2 2 D u = Div. D( Gradu ) = x x = u 2 + + k k x 12 x 22 x 32 2 u 3 Laplacien d’un Vecteur u(x) Laplacien et Rotationnel [Rot u ]k = eklm um xl [Rot (Rot u)]i =eijk x 12 + x 22 + x 32 Rot (Rot u ) = Grad(Div u ) - D u 2 2 ui 2 uj e um =(d d -d d ) um =[Grad(Divu )]i -[D u ]i = il jm im jl klm xj xl xj x 1 xi xj xj xj
 Haribo c'est beau la vie pour les grand et les petit
Haribo c'est beau la vie pour les grand et les petit Parts d una flor
Parts d una flor Allez vous en sur les places
Allez vous en sur les places Les constellations les plus connues
Les constellations les plus connues Qu'est-ce que tu aimes manger?
Qu'est-ce que tu aimes manger? Classes de mots variables et invariables
Classes de mots variables et invariables Les arguments pour tous les sujets
Les arguments pour tous les sujets Les lettres en français
Les lettres en français Preactionneurs
Preactionneurs Pronoms convenable
Pronoms convenable Les mots qu'on ne dit pas sont les fleurs du silence
Les mots qu'on ne dit pas sont les fleurs du silence Trouvez les réponses. écrivez-les en chiffres (numbers).
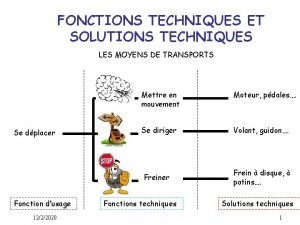
Trouvez les réponses. écrivez-les en chiffres (numbers). Fonctions et solutions techniques
Fonctions et solutions techniques Le volcan le plus dangereux du monde
Le volcan le plus dangereux du monde