Limitn vty Limitn vty tvrzen kter jsou dleit









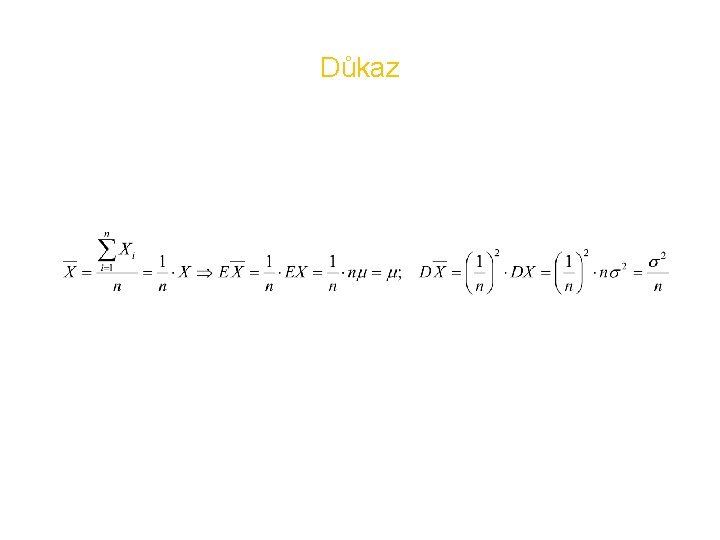









- Slides: 20

Limitní věty

Limitní věty • tvrzení, která jsou důležitá pro popis pravděpodobnostních modelů v případě rostoucího počtu náhodných pokusů

Konvergence podle pravděpodobnosti (stochastická konvergence) Je dána posloupnost náhodných veličin {Xn} a náhodná veličina X. Jestliže pro každé ε > 0 platí: , pak říkáme, že posloupnost náhodných veličin {Xn} konverguje k náhodné veličině X podle pravděpodobnosti.

Konvergence v distribuci Je dána posloupnost náhodných veličin {Xn}, posloupnost distribučních funkcí náhodných veličin {Xn}{Fn(x)} a náhodná veličina X, která má distribuční funkci F(x). Jestliže: , pak říkáme, že posloupnost náhodných veličin {Xn} konverguje k náhodné veličině X v distribuci a F(x) nazýváme asymptotickou distribuční funkcí.

Čebyševova nerovnost • odhaduje (velice hrubě) pravděpodobnost odchylky náhodné veličiny X od její střední hodnoty Nechť X je libovolná náhodná veličina se střední hodnotou EX a konečným rozptylem DX.

Litschmannová: Statistika I. – řešené příklady, kap. Limitní věty př. 8. 1, 8. 2

Centrální limitní věta • zabývá se konvergencí rozdělení k normálnímu rozdělení 2 dílčí formulace CLV: 1. ) Lindebergova-Lévyho věta 2. ) Moivreova-Laplaceova věta

Lindebergova-Lévyho věta (Rozdělení součtu NV) Jestliže X 1, X 2, …, Xn jsou nezávislé náhodné veličiny se stejným (libovolným) rozdělením, stejnými středními hodnotami a se stejnými (konečnými) rozptyly , pak jejich součet konverguje v distribuci k normálnímu rozdělení o parametrech: nμ; nσ2. {Xn}: - nezávislé NV - NV se stejným typem rozdělení - EX 1=EX 2=…=EXn - DX 1=DX 2=…=DXn < ∞, Pak:

Důsledek Linderbergovy-Lévyho věty (Rozdělení průměru náhodných veličin) Jestliže X 1, X 2, …, Xn jsou nezávislé náhodné veličiny se stejným (libovolným) rozdělením, stejnými středními hodnotami a se stejnými (konečnými) rozptyly , pak jejich průměr konverguje v distribuci k normálnímu rozdělení o parametrech: μ; σ2/n. {Xn}: - nezávislé NV - NV se stejným typem rozdělení - EX 1=EX 2=…=EXn - DX 1=DX 2=…=DXn < ∞, Pak:
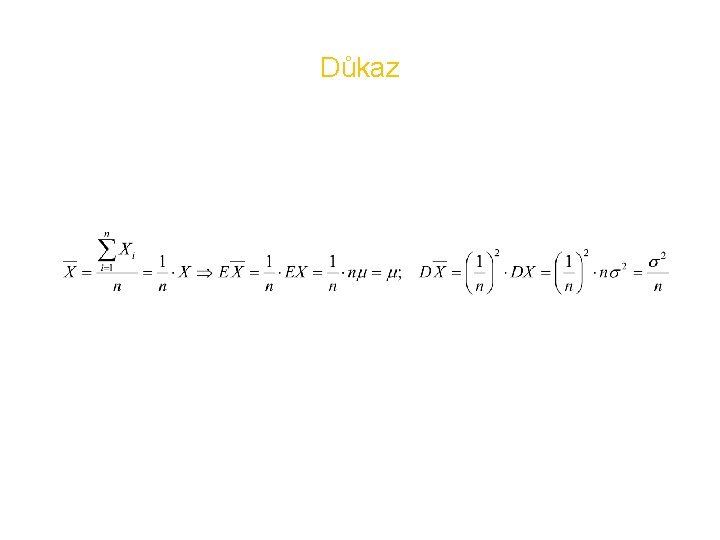
Důkaz

Litschmannová: Statistika I. – řešené příklady, kap. Limitní věty př. 8. 3, 8. 4, 8. 7

Příklad • Dlouhodobým průzkumem bylo zjištno, že doba potřebná k objevení a odstranní poruchy stroje má střední hodnotu 40 minut a směrodatnou odchylku 30 minut. Jaká je pravaděpodobnost, že doba potřebná k objevení a opravení 100 poruch nepřekročí 70 hodin?

Příklad Životnost elektrického holícího strojku Adam má exponenciální rozdělení se střední hodnotou 2 roky. Určete pravděpodobnost, že průměrná životnost 150 -ti prodaných strojků Adam bude vyšší než 27 měsíců.

Moivreova-Laplaceova věta • tato věta vyjadřuje konvergenci binomického rozdělení k normálnímu rozdělení , pak pro dostatečně velká n: Aproximace dává dobré výsledky, když: nebo

Aproximace Poissonova rozdělením normálním , pak pro dostatečně velké t platí, že X můžeme aproximovat norm. rozdělením s parametry:

Aproximace průměrného počtu výskytu události za časovou jednotku normálním rozdělením Y. . . počet výskytu události za časovou jednotku, X lze aproximovat normálním rozdělením, , pak:

Oprava na spojitost (u pravděpodobnostní funkce): Je-li X diskrétní náhodná veličina, pak: Obecně – oprava na spojitost: Posouzení vhodnosti použití opravy na spojitost provádíme vždy při řešení konkrétního příkladu důsledným převodem pravděpodobnosti výskytu náhodné veličiny na nějakém intervalu na vztah mezi distribučními funkcemi v příslušných bodech.

Litschmannová: Statistika I. – řešené příklady, kap. Limitní věty př. 8. 5, 8. 6

Příklad • Na telefonní ústřednu je napojeno 3000 účastníků. Každý z nich bude volat telefonní ústřednu během hodiny s pravděpodobností 10%. Jaká je pravděpodobnost, že během následující hodiny zavolá ústřednu: a) právě 300 účastníků? b) více než 310 účastníků? c) mezi 200 a 450 účastníky(včetně)?

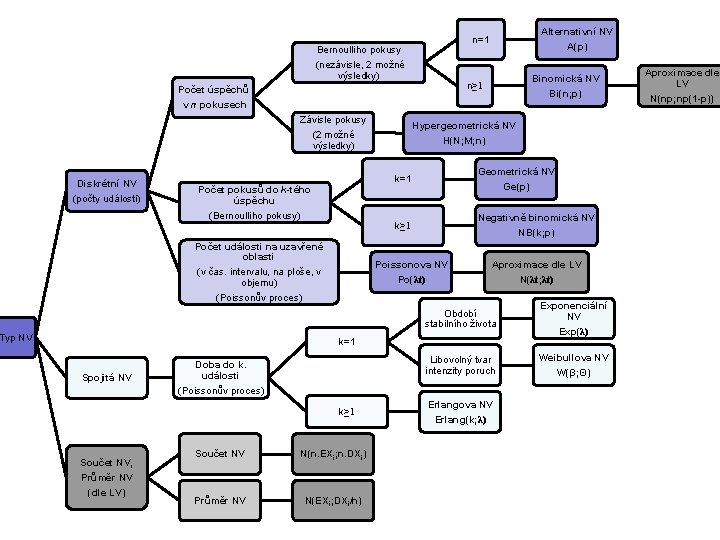
Bernoulliho pokusy (nezávisle, 2 možné výsledky) Diskrétní NV (počty události) Počet pokusů do k-tého úspěchu (Bernoulliho pokusy) Počet události na uzavřené oblasti (v čas. intervalu, na ploše, v objemu) (Poissonův proces) Typ NV Binomická NV Bi(n; p) n≥ 1 Počet úspěchů v n pokusech Závisle pokusy (2 možné výsledky) Alternativní NV A(p) n=1 Hypergeometrická NV H(N; M; n) k=1 Geometrická NV Ge(p) k≥ 1 Negativně binomická NV NB(k; p) Poissonova NV Po(λt) Aproximace dle LV N(λt; λt) Období stabilního života Exponenciální NV Exp(λ) Libovolný tvar intenzity poruch Weibullova NV W(β; Θ) k=1 Spojitá NV Doba do k. události (Poissonův proces) k≥ 1 Součet NV, Průměr NV (dle LV) Součet NV N(n. EXi; n. DXi) Průměr NV N(EXi; DXi/n) Erlangova NV Erlang(k; λ) Aproximace dle LV N(np; np(1 -p))
 Atlas kanada
Atlas kanada částice
částice Prérie a pampy
Prérie a pampy Každé dva obdélníky jsou podobné
Každé dva obdélníky jsou podobné Shodnost trojúhelníků příklady
Shodnost trojúhelníků příklady Proč jsou dráty elektrického vedení prověšené
Proč jsou dráty elektrického vedení prověšené Slyšel jsi někdy šakali vytí
Slyšel jsi někdy šakali vytí Jarni mesice jsou
Jarni mesice jsou Halogenidy zástupci
Halogenidy zástupci Jakou látkou jsou obaleny spojovací vodiče
Jakou látkou jsou obaleny spojovací vodiče Antilopa
Antilopa Máma táta véna jsou podstatná jména
Máma táta véna jsou podstatná jména Co jsou to soli
Co jsou to soli Sos význam
Sos význam Co jsou to alkany
Co jsou to alkany Vývržky sov
Vývržky sov Jaké jsou oceány
Jaké jsou oceány Inovace jsou in testy
Inovace jsou in testy Vidová dvojice
Vidová dvojice K
K Co jsou částice
Co jsou částice