Lesson 7 2 The Pythagorean Theorem Lesson 7

Lesson 7 -2 The Pythagorean Theorem Lesson 7 -2: The Pythagorean Theorem 1

Anatomy of a right triangle • The hypotenuse of a right triangle is the longest side. It is opposite the right angle. • The other two sides are legs. They form the right angle. leg hypotenuse leg Lesson 7 -2: The Pythagorean Theorem 2

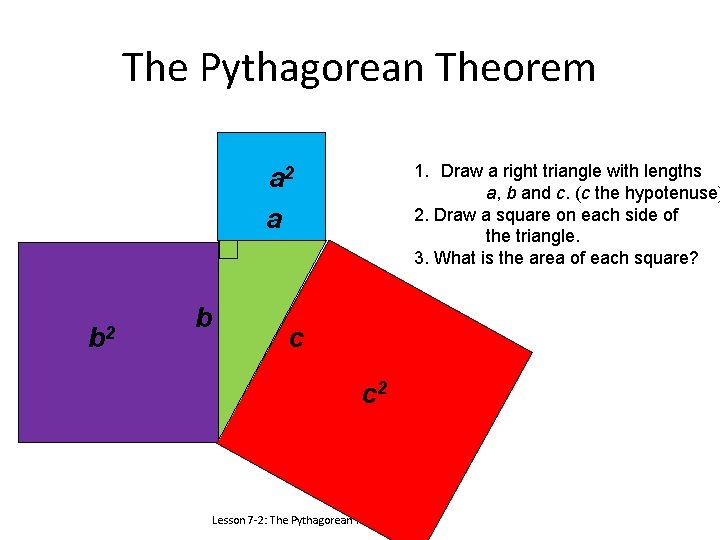
The Pythagorean Theorem 1. Draw a right triangle with lengths a, b and c. (c the hypotenuse) 2. Draw a square on each side of the triangle. 3. What is the area of each square? a 2 a b 2 b c c 2 Lesson 7 -2: The Pythagorean Theorem

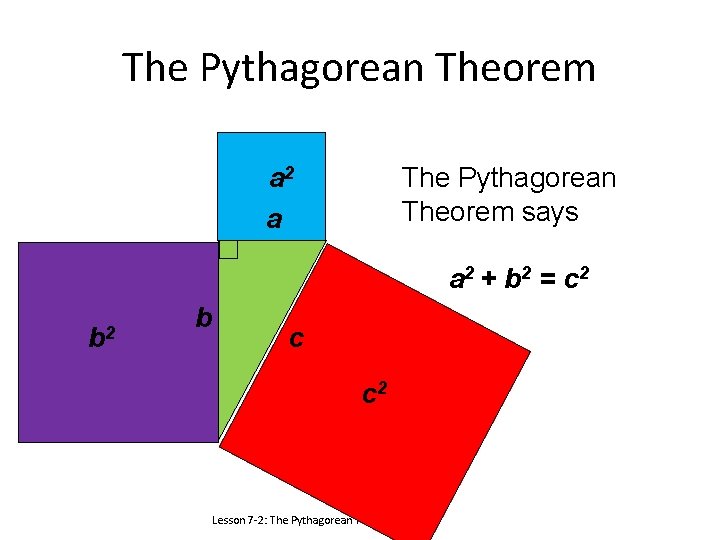
The Pythagorean Theorem a 2 a The Pythagorean Theorem says a 2 + b 2 = c 2 b c c 2 Lesson 7 -2: The Pythagorean Theorem

Proofs of the Pythagorean Theorem Proof 1 Proof 2 Proof 3 Lesson 7 -2: The Pythagorean Theorem 5

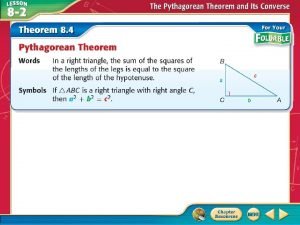
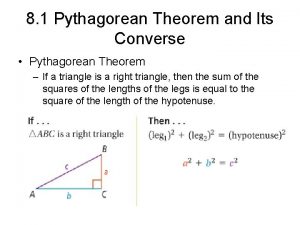
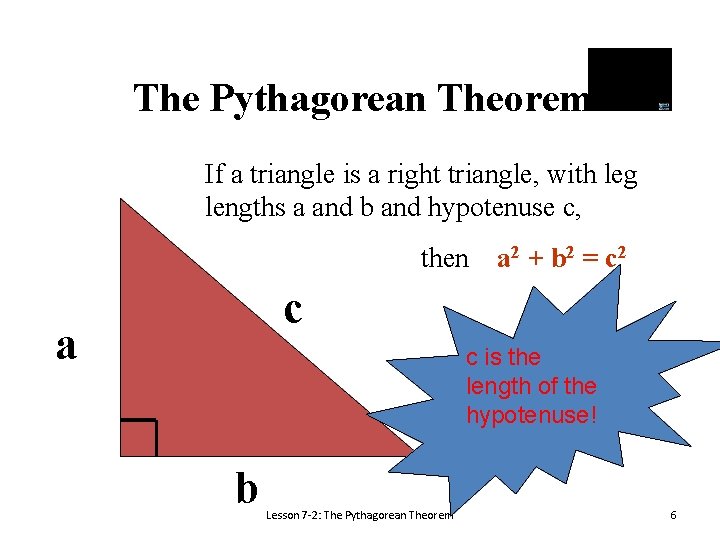
The Pythagorean Theorem If a triangle is a right triangle, with leg lengths a and b and hypotenuse c, then a 2 + b 2 = c 2 c a c is the length of the hypotenuse! b Lesson 7 -2: The Pythagorean Theorem 6

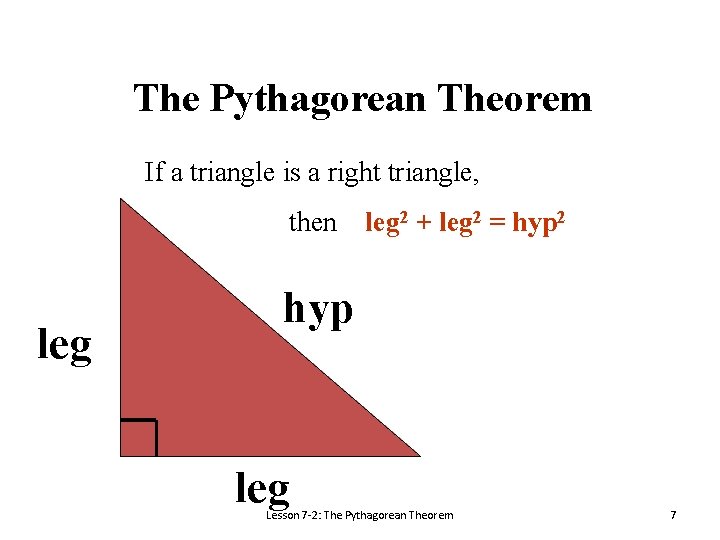
The Pythagorean Theorem If a triangle is a right triangle, then leg 2 + leg 2 = hyp 2 hyp leg Lesson 7 -2: The Pythagorean Theorem 7

Example In the following figure if a = 3 and b = 4, Find c. leg 2 + leg 2 = hyp 2 32 + 42 = C 2 9 + 16 = C 2 c a 25 = C 2 5 = C b Lesson 7 -2: The Pythagorean Theorem 8

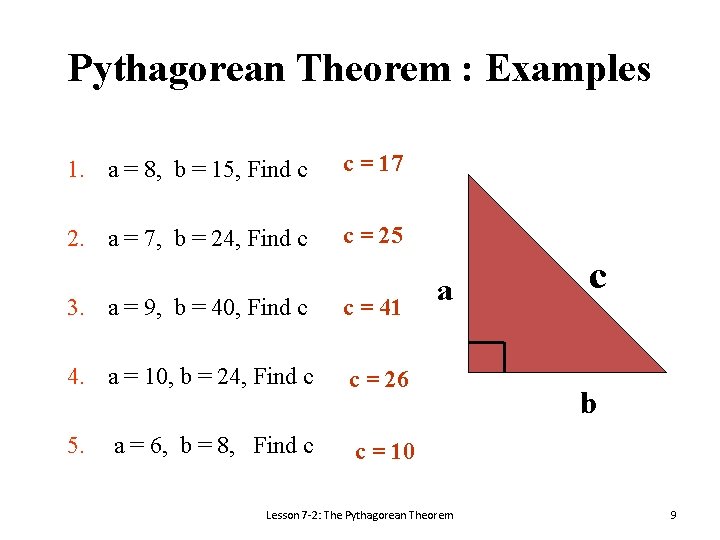
Pythagorean Theorem : Examples 1. a = 8, b = 15, Find c c = 17 2. a = 7, b = 24, Find c c = 25 3. a = 9, b = 40, Find c c = 41 4. a = 10, b = 24, Find c c = 26 5. c = 10 a = 6, b = 8, Find c a Lesson 7 -2: The Pythagorean Theorem c b 9

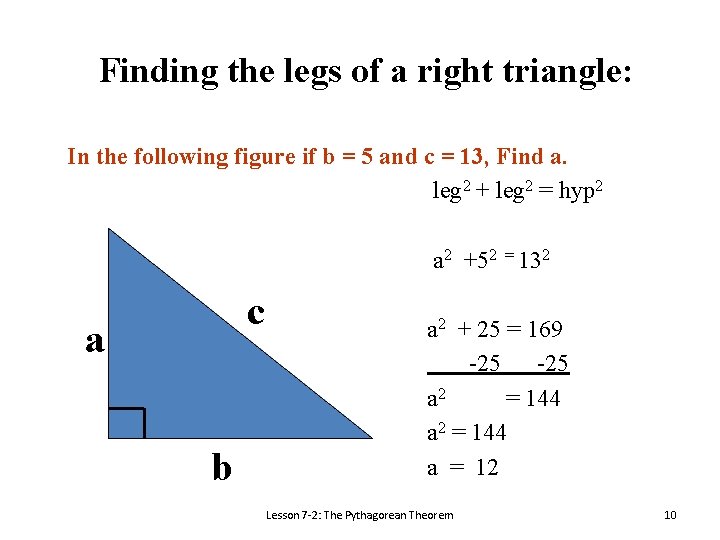
Finding the legs of a right triangle: In the following figure if b = 5 and c = 13, Find a. leg 2 + leg 2 = hyp 2 a 2 +52 = 132 c a b a 2 + 25 = 169 -25 a 2 = 144 a = 12 Lesson 7 -2: The Pythagorean Theorem 10

More Examples: 1) 2) 3) 4) 5) 6) 7) 8) a=8, c =10 , Find b a=15, c=17 , Find b b =10, c=26 , Find a a=15, b=20, Find c a =12, c=16, Find b b =5, c=10, Find a a =6, b =8, Find c a=11, c=21, Find b b=6 b=8 a = 24 c = 25 a = 8. 7 c = 10 c a b Lesson 7 -2: The Pythagorean Theorem 11

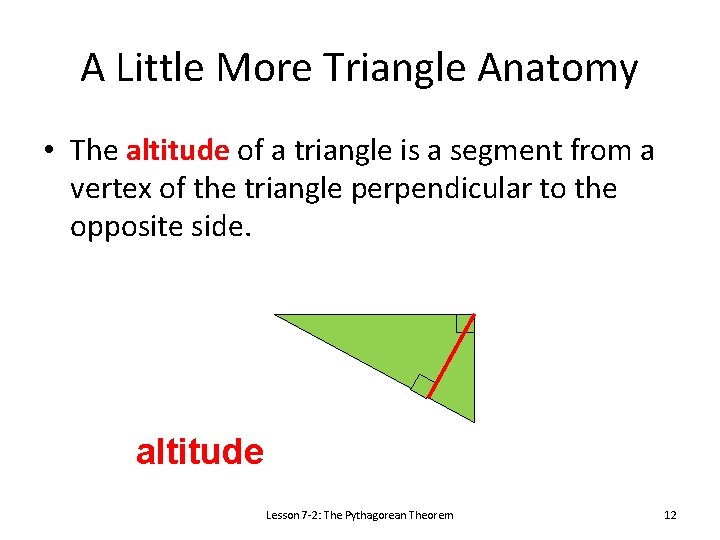
A Little More Triangle Anatomy • The altitude of a triangle is a segment from a vertex of the triangle perpendicular to the opposite side. altitude Lesson 7 -2: The Pythagorean Theorem 12

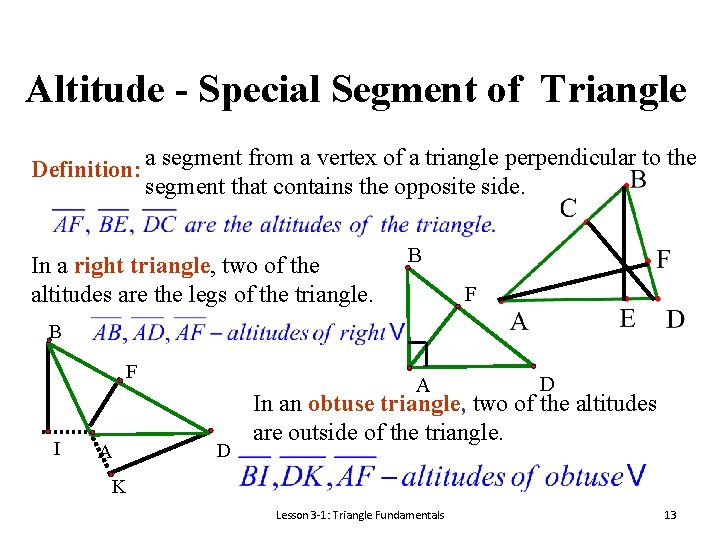
Altitude - Special Segment of Triangle Definition: a segment from a vertex of a triangle perpendicular to the segment that contains the opposite side. In a right triangle, two of the altitudes are the legs of the triangle. B F I A A D D In an obtuse triangle, two of the altitudes are outside of the triangle. K Lesson 3 -1: Triangle Fundamentals 13

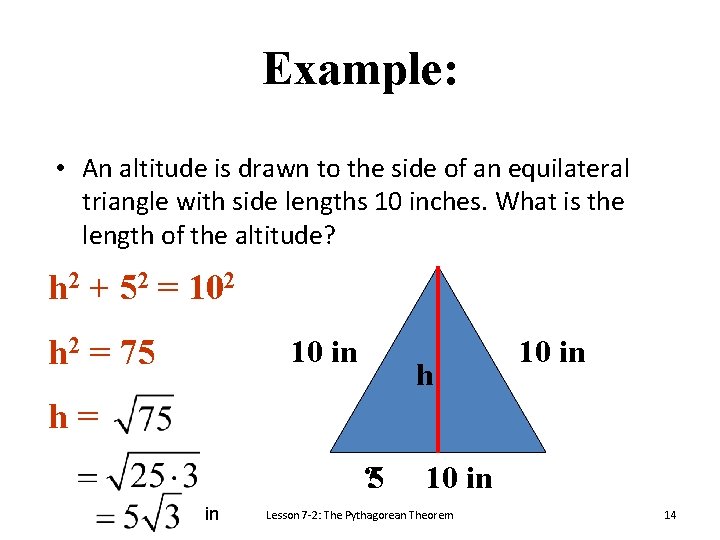
Example: • An altitude is drawn to the side of an equilateral triangle with side lengths 10 inches. What is the length of the altitude? h 2 + 52 = 102 h 2 = 75 10 in h= ? 5 in 10 in Lesson 7 -2: The Pythagorean Theorem 14

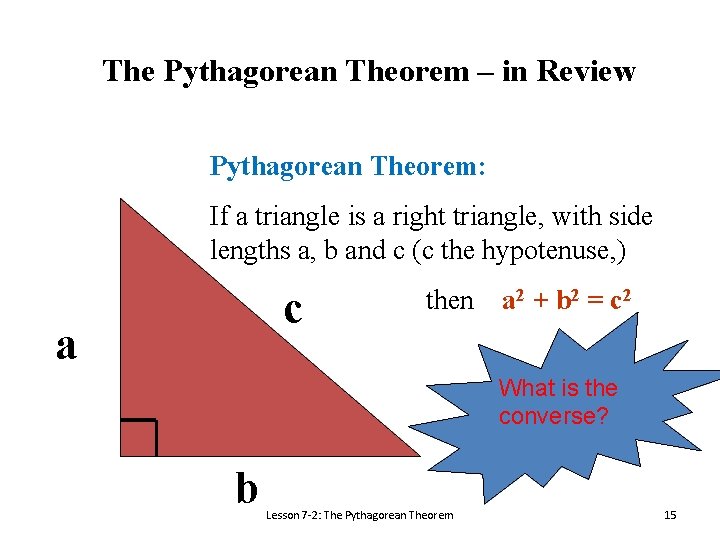
The Pythagorean Theorem – in Review Pythagorean Theorem: If a triangle is a right triangle, with side lengths a, b and c (c the hypotenuse, ) c a then a 2 + b 2 = c 2 What is the converse? b Lesson 7 -2: The Pythagorean Theorem 15

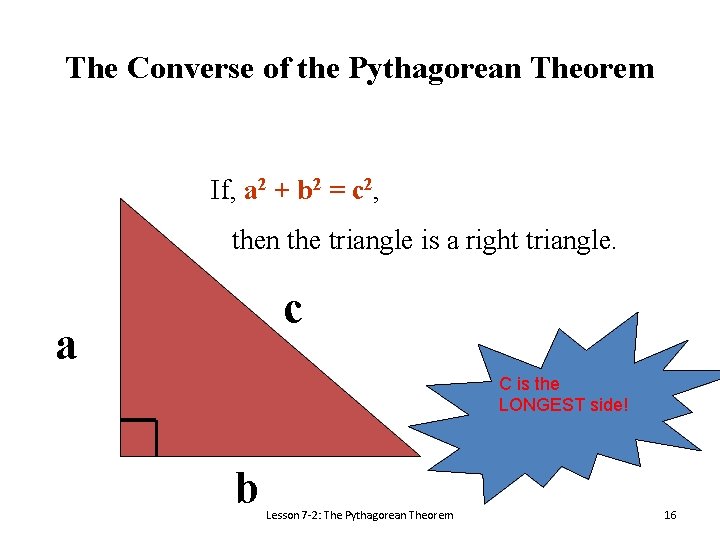
The Converse of the Pythagorean Theorem If, a 2 + b 2 = c 2, then the triangle is a right triangle. c a C is the LONGEST side! b Lesson 7 -2: The Pythagorean Theorem 16

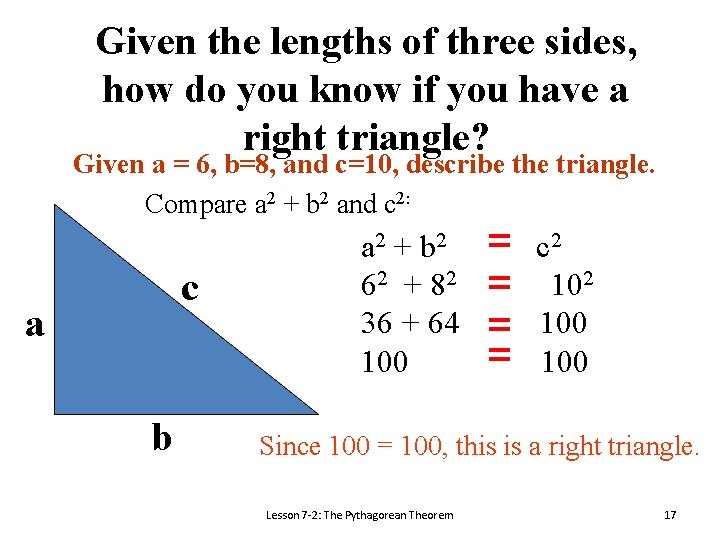
Given the lengths of three sides, how do you know if you have a right triangle? Given a = 6, b=8, and c=10, describe the triangle. Compare a 2 + b 2 and c 2: c a b a 2 + b 2 62 + 82 36 + 64 100 = = c 2 100 100 Since 100 = 100, this is a right triangle. Lesson 7 -2: The Pythagorean Theorem 17

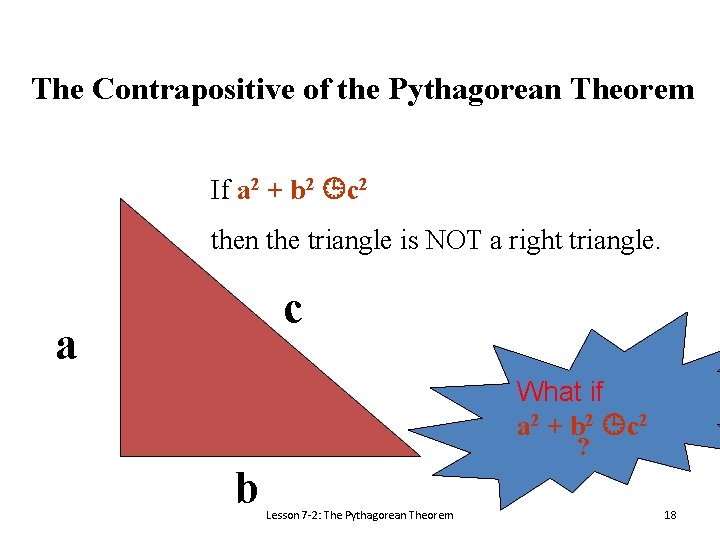
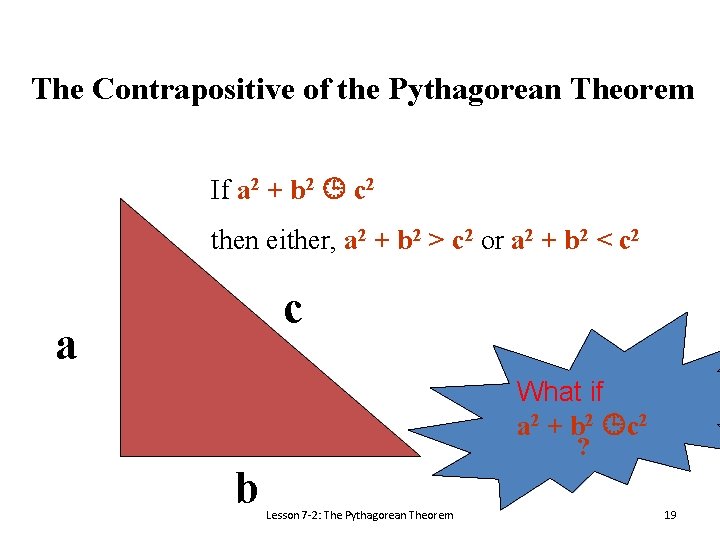
The Contrapositive of the Pythagorean Theorem If a 2 + b 2 c 2 then the triangle is NOT a right triangle. c a What if a 2 + b 2 c 2 ? b Lesson 7 -2: The Pythagorean Theorem 18

The Contrapositive of the Pythagorean Theorem If a 2 + b 2 c 2 then either, a 2 + b 2 > c 2 or a 2 + b 2 < c 2 c a What if a 2 + b 2 c 2 ? b Lesson 7 -2: The Pythagorean Theorem 19

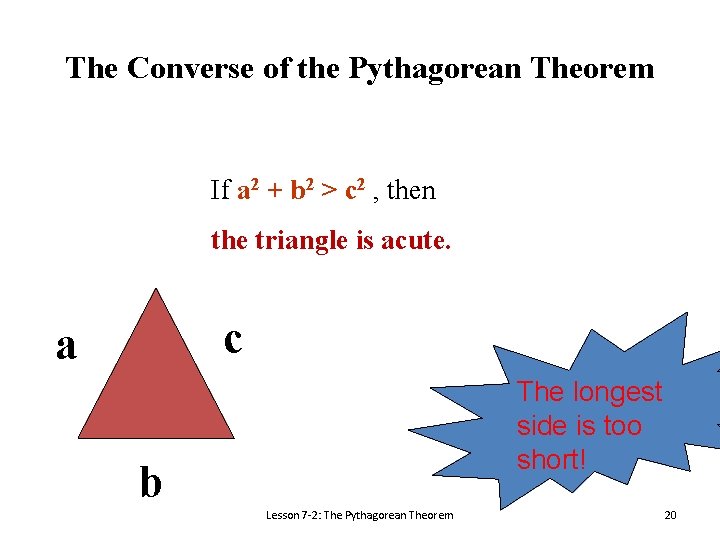
The Converse of the Pythagorean Theorem If a 2 + b 2 > c 2 , then the triangle is acute. c a The longest side is too short! b Lesson 7 -2: The Pythagorean Theorem 20

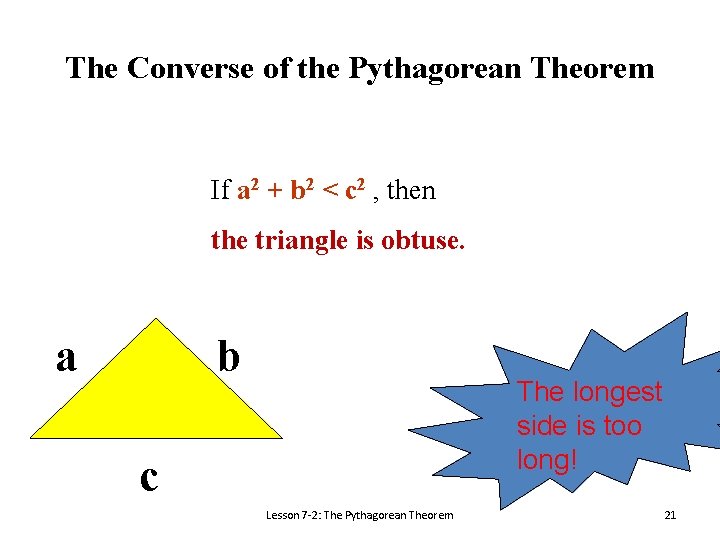
The Converse of the Pythagorean Theorem If a 2 + b 2 < c 2 , then the triangle is obtuse. a b The longest side is too long! c Lesson 7 -2: The Pythagorean Theorem 21

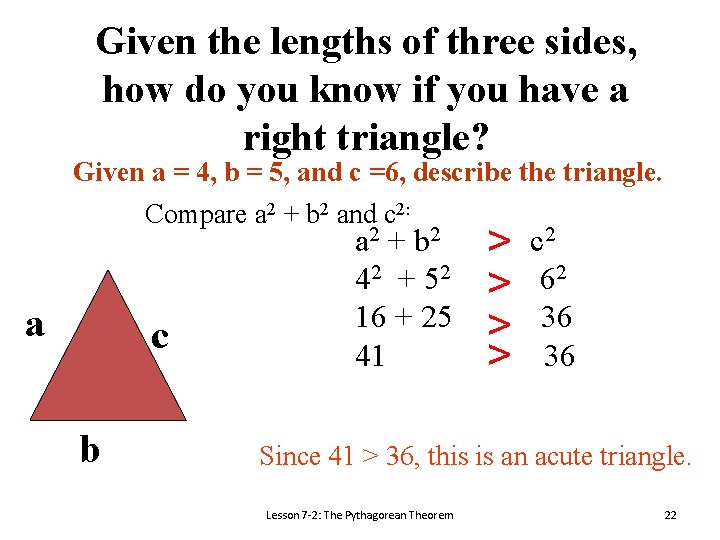
Given the lengths of three sides, how do you know if you have a right triangle? Given a = 4, b = 5, and c =6, describe the triangle. Compare a 2 + b 2 and c 2: a c b a 2 + b 2 42 + 52 16 + 25 41 > > c 2 62 36 36 Since 41 > 36, this is an acute triangle. Lesson 7 -2: The Pythagorean Theorem 22

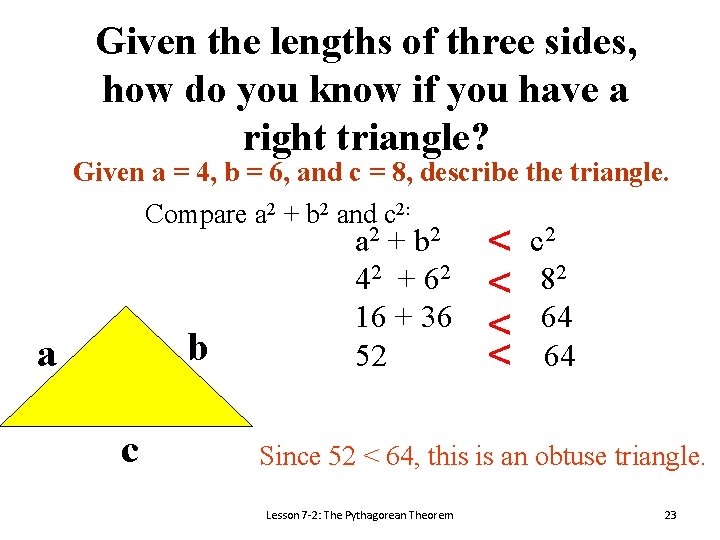
Given the lengths of three sides, how do you know if you have a right triangle? Given a = 4, b = 6, and c = 8, describe the triangle. Compare a 2 + b 2 and c 2: b a c a 2 + b 2 42 + 62 16 + 36 52 < < c 2 82 64 64 Since 52 < 64, this is an obtuse triangle. Lesson 7 -2: The Pythagorean Theorem 23

Describe the following triangles as acute, right, or obtuse right 1) 9, 40, 41 obtuse 2) 15, 20, 10 obtuse 3) 2, 5, 6 4) 12, 16, 20 right 5) 14, 12, 11 acute 6) 2, 4, 3 obtuse 7) 1, 7, 7 acute 8) 90, 150, 120 c a right Lesson 7 -2: The Pythagorean Theorem b 24

Application The Distance Formula

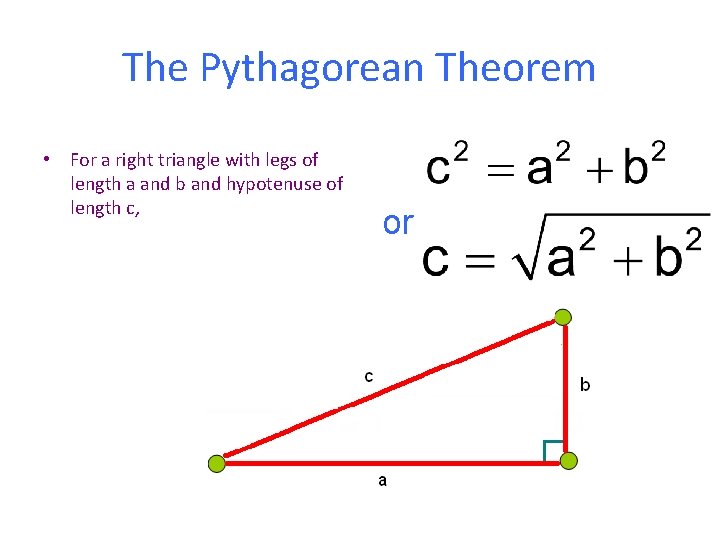
The Pythagorean Theorem • For a right triangle with legs of length a and b and hypotenuse of length c, or

The x-axis • Start with a horizontal number line which we will call the xaxis. • We know how to measure the distance between two points on a number line. x Take the absolute value of the difference: │a – b │ │ – 4 – 9 │= │ – 13 │ = 13

The y-axis • Add a vertical number line which we will call the y-axis. • Note that we can measure the distance between two points on this number line also. y x

The Coordinate Plane We call the x-axis together with the y-axis the coordinate plane. y x

Coordinates / Ordered Pair • Coordinates – numbers that identify the position of a point • Ordered Pair – a pair of numbers (xcoordinate, y-coordinate) identifying a point’s position Identify some coordinates and ordered pairs in the diagram. Diagram is from the website www. ezgeometry. com.

Finding Distance in The Coordinate Plane We can find the distance between any two points in the coordinate plane by using the Ruler Postulate AND the Pythagorean Theorem. y ? x

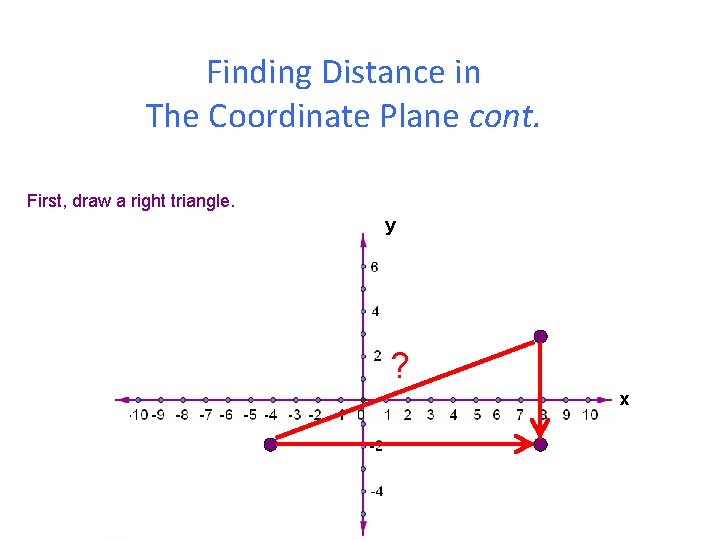
Finding Distance in The Coordinate Plane cont. First, draw a right triangle. y ? x

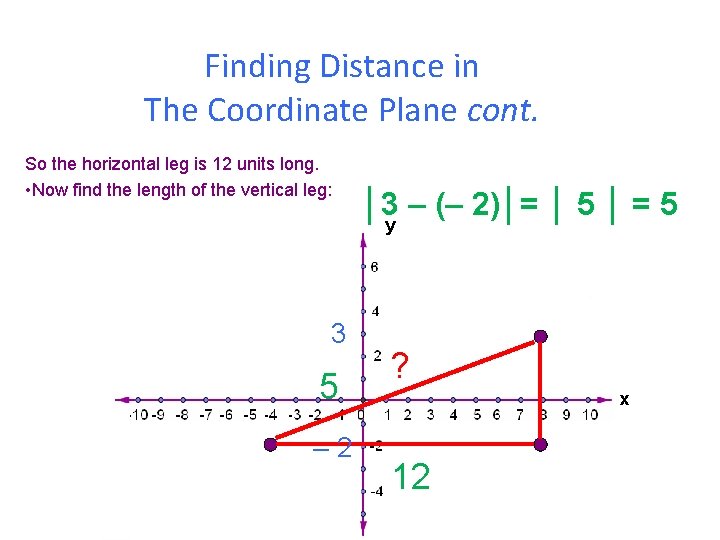
Finding Distance in The Coordinate Plane cont. Next, find the lengths of the two legs. • First, the horizontal leg: │(– 4) – 8│= │– 12│ = 12 y – 4 12 ? 8 x

Finding Distance in The Coordinate Plane cont. So the horizontal leg is 12 units long. • Now find the length of the vertical leg: │3 – (– 2)│= │ 5 │ = 5 y 3 5 – 2 ? x 12

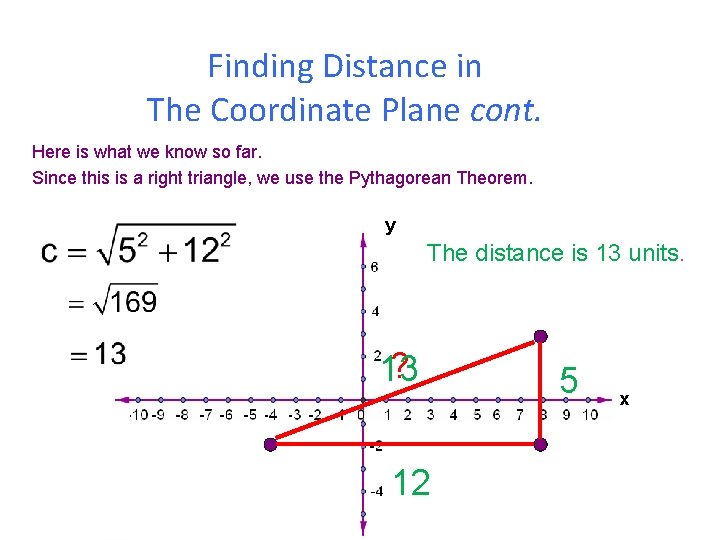
Finding Distance in The Coordinate Plane cont. Here is what we know so far. Since this is a right triangle, we use the Pythagorean Theorem. y The distance is 13 units. ? 13 12 5 x

The Distance Formula Instead of drawing a right triangle and using the Pythagorean Theorem, we can use the following formula: distance = where (x 1, y 1) and (x 2, y 2) are the ordered pairs corresponding to the two points. So let’s go back to the example.

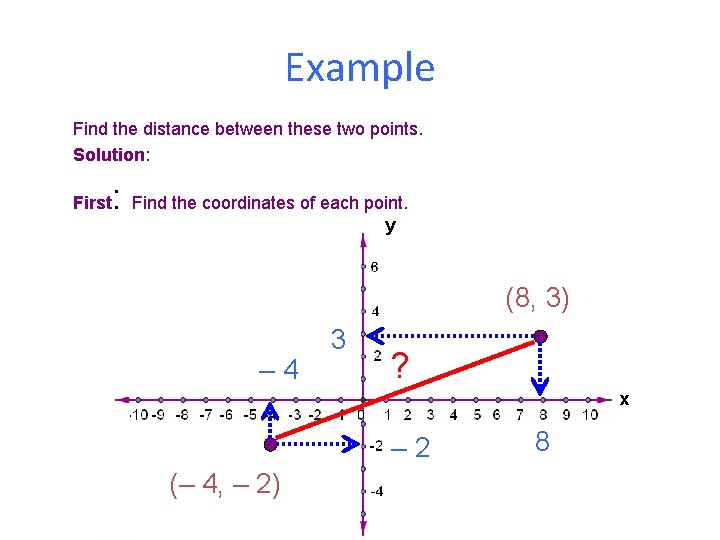
Example Find the distance between these two points. Solution: First : Find the coordinates of each point. y (8, 3) – 4 3 ? x – 2 (– 4, – 2) 8

Example Find the distance between these two points. Solution: First: Find the coordinates of each point. (x 1, y 1) = (-4, -2) y (x 2, y 2) = (8, 3) ? x (– 4, – 2)

Example cont. Solution cont. Then: Since the ordered pairs are (x 1, y 1) = (-4, -2) and (x 2, y 2) = (8, 3) Plug in x 1 = -4, y 1 = -2, x 2 = 8 and y 2 = 3 into distance = = 13