Lesson 4 2 Mean Value Theorem and Rolles

Lesson 4 -2 Mean Value Theorem and Rolle’s Theorem

Quiz • Homework Problem: Related Rates 3 -10 Gravel is being dumped from a conveyor belt at a rate of 30 ft³/min, and forms a pile in shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high? • Reading questions: – What were the names of the two theorems in section 4. 2? – What pre-conditions (hypotheses) do the Theorems have in common?

Objectives • Understand Rolle’s Theorem • Understand Mean Value Theorem

Vocabulary • Existence Theorem – a theorem that guarantees that there exists a number with a certain property, but it doesn’t tell us how to find it.

Theorems Mean Value Theorem: Let f be a function that is a) continuous on the closed interval [a, b] b) differentiable on the open interval (a, b) then there is a number c in (a, b) such that f(b) – f(a) f’(c) = -------- or equivalently: f(b) – f(a) = f’(c)(b – a) b – a Rolle’s Theorem: Let f be a function that is a) continuous on the closed interval [a, b] b) differentiable on the open interval (a, b) c) f(a) = f(b) then there is a number c in (a, b) such that f’(c) = 0

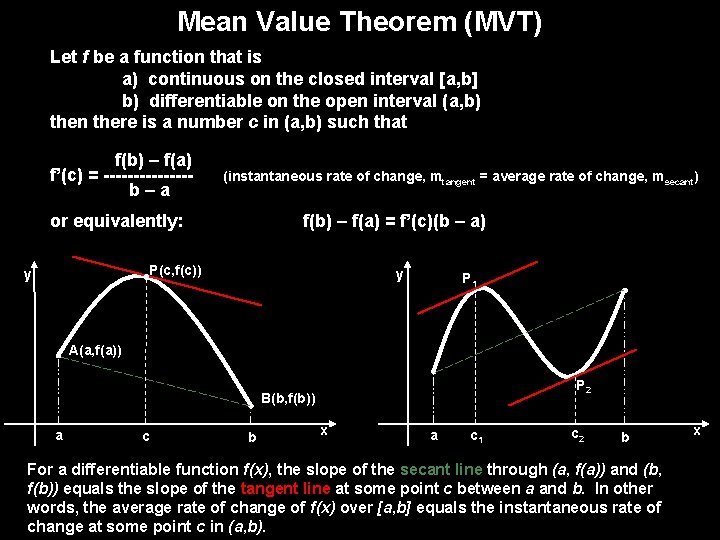
Mean Value Theorem (MVT) Let f be a function that is a) continuous on the closed interval [a, b] b) differentiable on the open interval (a, b) then there is a number c in (a, b) such that f(b) – f(a) f’(c) = -------- (instantaneous rate of change, mtangent = average rate of change, msecant) b – a or equivalently: f(b) – f(a) = f’(c)(b – a) P(c, f(c)) y y P 1 A(a, f(a)) P 2 B(b, f(b)) a c b x a c 1 c 2 b For a differentiable function f(x), the slope of the secant line through (a, f(a)) and (b, f(b)) equals the slope of the tangent line at some point c between a and b. In other words, the average rate of change of f(x) over [a, b] equals the instantaneous rate of change at some point c in (a, b). x

Example 1 Verify that the mean value theorem (MVT) holds for f(x) = -x² + 6 x – 6 on [1, 3]. a) continuous on the closed interval [a, b] polynomial b) differentiable on the open interval (a, b) polynomial f’(x) = -2 x + 6 f(b) – f(a) = f(3) – f(1) = 3 – (-1) = 4 f(b) – f(a) / (b – a) = 4/2 = 2 f’(x) = 2 = 6 – 2 x so -4 = -2 x 2 = x

Example 2 Find the number that satisfies the MVT on the given interval or state why theorem does not apply. f(x) = x 2/5 on [0, 32] a) continuous on the closed interval [a, b] ok b) differentiable on the open interval (a, b) ok on open f’(x) = (2/5)x-3/5 f(b) – f(a) = f(32) – f(0) = 4 – 0 = 4 f(b) – f(a) / (b – a) = 4/32 = 0. 125 f’(x) = 0. 125 = (2/5)x-3/5 so x = 6. 94891

Example 3 Find the number that satisfies the MVT on the given interval or state why theorem does not apply. f(x) = x + (1/x) on [1, 3] a) continuous on the closed interval [a, b] ok b) differentiable on the open interval (a, b) ok on open f’(x) = 1 – x-2 f(b) – f(a) = f(3) – f(1) = 10/3 – 2 = 4/3 f(b) – f(a) / (b – a) = (7/3)/2 = 2/3 f’(x) = 2/3 = 1 – x-2 so x-2 = 1/3 x² = 3 x= 3 = 1. 732

Example 4 Find the number that satisfies the MVT on the given interval or state why theorem does not apply. f(x) = x 1/2 + 2(x – 3)1/3 on [1, 9] a) continuous on the closed interval [a, b] ok b) differentiable on the open interval (a, b) vertical tan f’(x) = 1/2 x-1/2 + 2/3(x – 3)-2/3 f’(x) undefined at x = 3 (vertical tangent) MVT does not apply

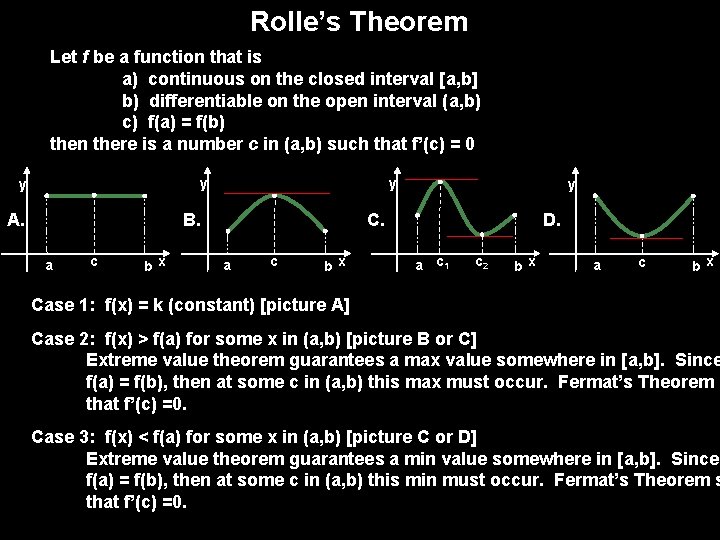
Rolle’s Theorem Let f be a function that is a) continuous on the closed interval [a, b] b) differentiable on the open interval (a, b) c) f(a) = f(b) then there is a number c in (a, b) such that f’(c) = 0 y y A. y C. B. a c bx y a c bx D. a c 1 c 2 bx a c bx Case 1: f(x) = k (constant) [picture A] Case 2: f(x) > f(a) for some x in (a, b) [picture B or C] Extreme value theorem guarantees a max value somewhere in [a, b]. Since f(a) = f(b), then at some c in (a, b) this max must occur. Fermat’s Theorem s that f’(c) =0. Case 3: f(x) < f(a) for some x in (a, b) [picture C or D] Extreme value theorem guarantees a min value somewhere in [a, b]. Since f(a) = f(b), then at some c in (a, b) this min must occur. Fermat’s Theorem s that f’(c) =0.

Example 5 Determine whether Rolle’s Theorem’s hypotheses are satisfied &, if so, find a number c for which f’(c) = 0. f(x) = x² + 9 on [-3, 3] a) continuous on the closed interval [a, b] polynomial b) differentiable on the open interval (a, b) polynomial c) f(a) = f(b) f(-3) = 18 f(3) = 18 f’(x) = 2 x f’(x) = 0 when x = 0 0 in the interval [-3, 3]

Example 6 Determine whether Rolle’s Theorem’s hypotheses are satisfied &, if so, find a number c for which f’(c) = 0. f(x) = x³ - 2 x² - x + 2 on [-1, 2] a) continuous on the closed interval [a, b] polynomial b) differentiable on the open interval (a, b) polynomial c) f(a) = f(b) f(-1) = 0 f(2) = 0 f’(x) = 3 x² - 4 x – 1 f’(x) = 0 when x = ( 7 + 2)/3 = 1. 5486 f’(x) = 0 when x = -( 7 - 2)/3 = -0. 2153 and 1. 5486 in the interval [-1, 2]

Example 7 Determine whether Rolle’s Theorem’s hypotheses are satisfied &, if so, find a number c for which f’(c) = 0. f(x) = (x² - 1) / x on [-1, 1] a) continuous on the closed interval [a, b] no at x = 0 b) differentiable on the open interval (a, b) no at x = 0 c) f(a) = f(b) f(-1) = 0 f(1) = 0

Example 8 Determine whether Rolle’s Theorem’s hypotheses are satisfied &, if so, find a number c for which f’(c) = 0. f(x) = sin x on [0, π] a) continuous on the closed interval [a, b] ok b) differentiable on the open interval (a, b) ok c) f(a) = f(b) f(0) = 0 f(π) = 0 f’(x) = cos x f’(x) = 0 (or undefined) when x = π/2 in the interval [0, π]

Summary & Homework • Summary: – Mean Value and Rolle’s theorems are existance theorems – Each has some preconditions that must be met to be used • Homework: – pg 295 -296: 2, 7, 11, 12, 24