Rolles theorem and Mean Value Theorem Section 3

Rolle’s theorem and Mean Value Theorem (Section 3. 2) Alex Karassev

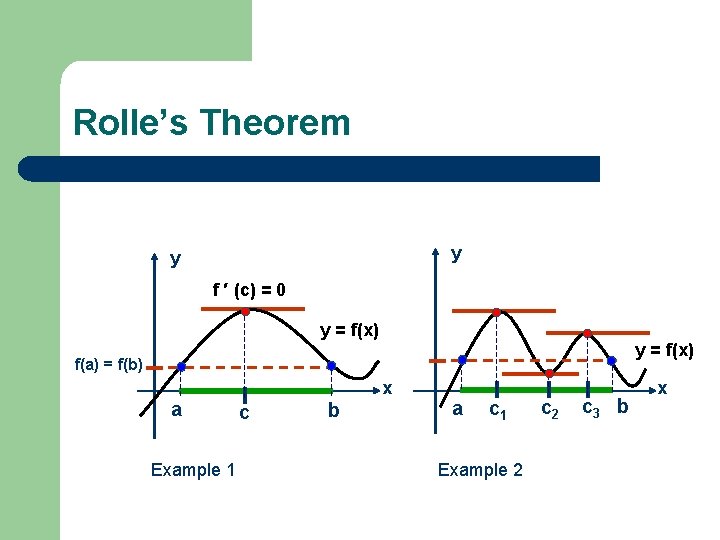
Rolle’s Theorem y y f ′ (c) = 0 y = f(x) f(a) = f(b) a Example 1 x c b a c 1 Example 2 c 3 b x

Rolles Theorem l Suppose f is a function such that y f ′ (c) = 0 f is continuous on [a, b] q differentiable at least in (a, b) q l If f(a) = f(b) then there exists at least one c in (a, b) such that f′(c) = 0 y = f(x) x a c b

Applications of Rolle’s Theorem l It is used in the prove of the Mean Value Theorem l Together with the Intermediate Value Theorem, it helps to determine exact number of roots of an equation

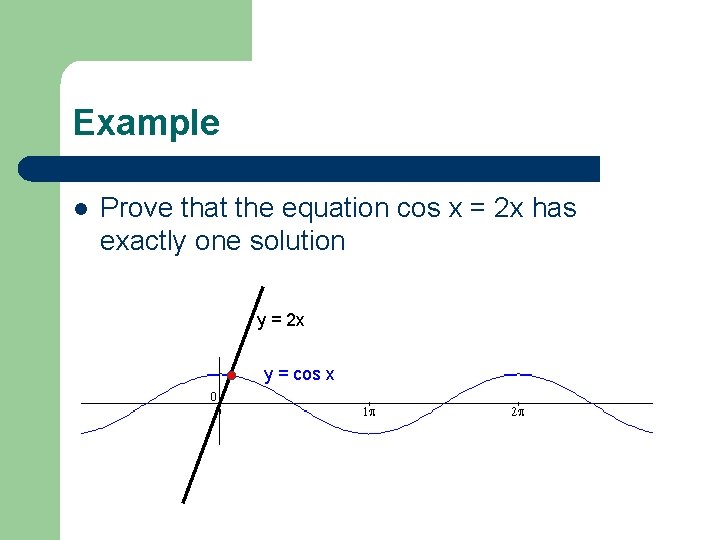
Example l Prove that the equation cos x = 2 x has exactly one solution y = 2 x y = cos x

Solution l cos x = 2 x has exactly one solution means two things: q It has a solution – can be proved using the IVT q It has no more than one solution – can be proved using Rolle's theorem

cos x = 2 x has a solution: Proof using the IVT l cos x = 2 x is equivalent to cos x – 2 x = 0 l Let f(x) = cos x – 2 x l f is continuous for all x, so the IVT can be used l f(0) = cos 0 – 2∙ 0 = 1 > 0 l f(π/2) = cos π/2 – 2 ∙ π/2 = 0 – π = – π < 0 l Thus by the IVT there exists c in [0, π/2] such that f(c) = 0, so the equation has a solution

f(x) = cos x – 2 x = 0 has no more than one solution: Proof by contradiction using Rolle's theorem l Assume the opposite: the equation has at least two solutions l Then there exist two numbers a and b s. t. a ≠ b and f(a) = f(b) = 0 l In particular, f(a) = f(b) l f(x) is differentiable for all x, and hence Rolle's theorem is applicable l By Rolle's theorem, there exists c in [a, b] such that f′(c) = 0 l Find the derivative: f ′ (x) = (cos x – 2 x) ′ = – sin x – 2 l So if we had f ′ (c) = 0 it would mean that –sin c – 2 = 0 or sin c = – 2, which is impossible! l Thus we obtained a contradiction l All our steps were logically correct so the fact that we obtained a contradiction means that our original assumption "the equation has at least two solutions" was wrong l Thus, the equation has no more than one solution!

f(x) = cos x – 2 x = 0 has no more than one solution: visualization If it had two roots, then there would exist a ≠ b such that f(a) = f(b) = 0 f ′ (c) = 0 y = f(x) a c b But f ′ (x) = (cos x – 2 x) ′ = – sin x – 2 So if we had f ′ (c) = 0 it would mean that –sin c – 2 = 0 or sin c = – 2, which is impossible

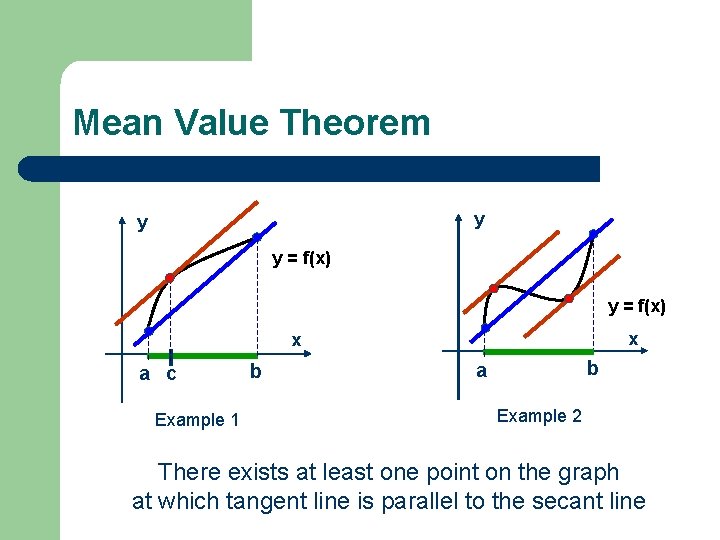
Mean Value Theorem y y y = f(x) x x a c Example 1 b b a Example 2 There exists at least one point on the graph at which tangent line is parallel to the secant line

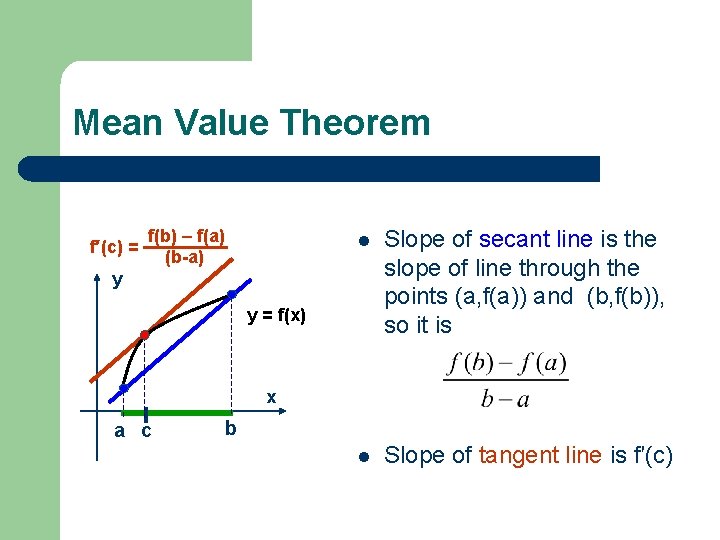
Mean Value Theorem f′(c) = f(b) – f(a) (b-a) l Slope of secant line is the slope of line through the points (a, f(a)) and (b, f(b)), so it is l Slope of tangent line is f′(c) y y = f(x) x a c b

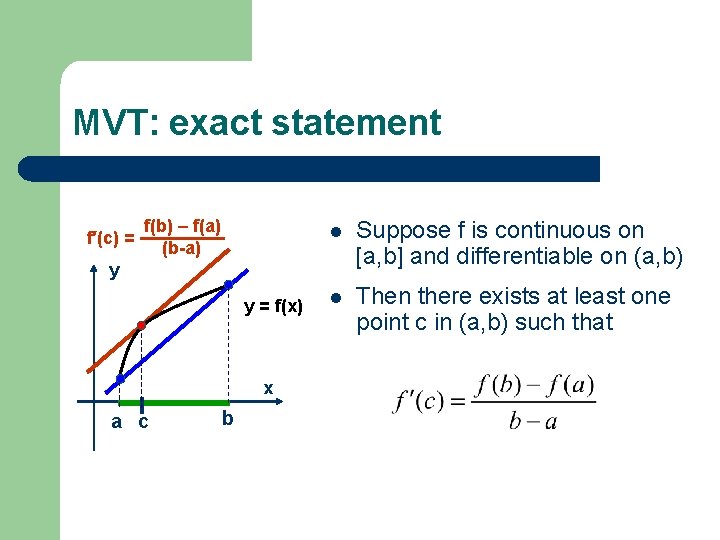
MVT: exact statement f′(c) = f(b) – f(a) (b-a) l Suppose f is continuous on [a, b] and differentiable on (a, b) l Then there exists at least one point c in (a, b) such that y y = f(x) x a c b

MVT: alternative formulations

Interpretation of the MVT using rate of change l Average rate of change is equal to the instantaneous rate of change f′(c) at some moment c l Example: suppose the cities A and B are connected by a straight road and the distance between them is 360 km. You departed from A at 1 pm and arrived to B at 5: 30 pm. Then MVT implies that at some moment your velocity v(t) = s′(t) was: (s(5. 5) – s(1)) / (5. 5 – 1) = 360 / 4. 5 = 80 km / h

Application of MVT Estimation of functions l Connection between the sign of derivative and behavior of the function: if f ′ > 0 function is increasing if f ′ < 0 function is decreasing l Error bounds for Taylor polynomials l

Example l l Suppose that f is differentiable for all x If f (5) = 10 and f ′ (x) ≤ 3 for all x, how small can f(-1) be?

Solution l MVT: f(b) – f(a) = f ′(c) (b – a) for some c in (a, b) l Applying MVT to the interval [ – 1, 5], we get: l f(5) – f(– 1) = f ′(c) (5 – (– 1)) = 6 f ′(c) ≤ 6∙ 3 = 18 l Thus f(5) – f(-1) ≤ 18 l Therefore f(-1) ≥ f(5) – 18 = 10 – 18 = – 8